Заавар.

Бодолт. Болно гэдгийг баталъя. $a$, $b$, $c$ гурвал дээр үйлдлийг $2009$ удаа давтахад $b+1$, $c$, $a-1$ тоонууд, $3\cdot 2009$ удаа давтахад $a-3$, $b+3$, $c$ тоонууд үүснэ. $$(a,b,c)\to\left(c,a-\frac{1}{2009},b+\frac{1}{2009}\right)\to\left(b+\frac{2}{2009},c,a-\frac{2}{2009}\right)\to\dots\to(b+1,c,a-1)$$ $$(a,b,c)\to\dots\to(b+1,c,a-1)\to\dots\to(c,a-2,b+2)\to\dots\to(a-3,a+3,c)$$ Эхний үйлдлийг $(1)$ үйлдэл, хоёр дахийг нь $(2)$ үйлдэл гэж нэрлэе. $(3k+4,3k+2,3k+3)$ гурвал дээр $(1)$ үйлдэл хийвэл $$(3k+4,3k+2,3k+3)\overset{(1)}{\longrightarrow}(3k+4,3k+2,3k+3)$$ болно. Иймд $1$, $2,\dots, 2011$ тоонуудаас $1$, $3$, $3$, $3$, $6$, $6$, $6,\dots, 2010$, $2010$, $2010$ үүснэ. $$(3k, 2013-3k, 1)\overset{(2)\times n}{\longrightarrow}(2013-3k, 3k, 1),\quad n=\frac{2013-6k}{3}=671-2k$$ тул $1$, $3$, $3$, $3$, $6$, $6$, $6,\dots, 2010$, $2010$, $2010$-ийг $1$, $2010$, $2010$, $2010,\dots, 6$, $6$, $6$, $3$, $3$, $3$ болгож чадна. $$(3k,3k,3k)\overset{(1)}{\longrightarrow}(3k+1,3k,3k-1)$$ тул $1$, $2010$, $2010$, $2010,\dots, 6$, $6$, $6$, $3$, $3$, $3$-ыг $1$, $2011$, $2010$, $2009, \dots, 7$, $6$, $5$, $4$, $3$, $2$ болгож чадна. Энэ нь цагийн зүүний эсрэг чиглэлд дугаарлалт юм.

Заавар.

Бодолт. $a(x)=x^{a_1}+x^{a_2}+\cdots+x^{a_n}$, $b(x)=x^{b_1}+x^{b_2}+\cdots+x^{b_n}\in\mathbb Z[x]$ олон гишүүнтүүдийг авъя. Эсрэгээс нь $a(x)\neq b(x)$ гэе. $$ [a(x)]^3=\big(\sum_{i=1}^n x^{a_i}\big)\big(\sum_{i\neq j}x^{a_i+a_j}+\sum_{i=1}^n x^{2a_i}\big)=$$ $$=\big(\sum_{i=1}^n x^{a_i}\big)\big(\sum_{i\neq j}x^{a_i+a_j}\big)+\big(\sum_{i=1}^n x^{a_i}\big)\big(\sum_{i=1}^n x^{2a_i}\big)=$$ $$=\big(\sum_{i\neq j\neq k}x^{a_i+a_j+a_k}+2\sum_{i\neq j} x^{a_i+2a_j}\big)+\big(\sum_{i\neq j} x^{a_i+2a_j}+\sum_{i=1}^n x^{3a_i}\big) $$ $$\sum_{i\neq j\neq k}x^{a_i+a_j+a_k}=[a(x)]^3-3a(x)a(x^2)+2a(x^3)$$ бодлогын нөхцөлөөс $$[a(x)]^3-3a(x)a(x^2)+2a(x^3)=[b(x)]^3-3b(x)b(x^2)+2b(x^3)$$ болно. $f(x)=a(x)-b(x)$ гэе. $f(1)=a(1)-b(1)=n-n=0$ байна. $f(x)=(x-1)^kh(x)$, $h(1)\neq0$ гэе. Тэгвэл $$ (a(x)-b(x))([a(x)]^2+a(x)b(x)+[b(x)]^2)-3(a(x)(a(x^2)-$$ $$-b(x^2))+b(x^2)(a(x)-b(x)))+2(a(x^3)-b(x^3))=0 $$ тул $$ (x-1)^k h(x)([a(x)]^2+a(x)b(x)+[b(x)]^2)-3(a(x)(x^2-1)^kh(x^2)+$$ $$+b(x^2)(x-1)^kh(x))+2(x^3-1)^kh(x^3)=0$$ иймд \begin{align*} h(x)([a(x)]^2&+a(x)b(x)+[b(x)]^2)-3(a(x)(x+1)^kh(x^2)+\\ &+b(x^2)h(x))+2(x^2+x+1)^kh(x^3)=0 \end{align*} $x=1$ гэвэл $3n^2-3(n\cdot 2^k+n)+2\cdot3^k=0$ буюу $n^2-n(2^k+1)+2\cdot 3^{k-1}=0$ тул $n\mid 2\cdot 3^{k-1}$ болж $(n,6)=1$-д зөрчиж байна.

Заавар.

Бодолт. $A$ дээр төвтэй ирверс хийе. Тэгвэл $\omega_A\to \ell_A$, $\omega_B\to\omega_{B'}$, $\omega\to \ell$, $\omega_C\to\omega_{C'}$, $\omega_D\to\omega_{D'}$, $\omega_{E}\to\omega_{E'}$, $\omega_F\to\omega_{F'}$ болно.

$\omega_A$, $\omega$ нь $A$ цэгт шүргэлцэх тул $\ell_A\parallel \ell$ болно. $\omega_{F'}$, $\omega_{B'}$ нь $\ell_A$, $\ell$-г шүргэх тул $R_B=R_F=R$ байна.

$\omega_{C'}$-ийн радиус $r_C$, $\omega_{D'}$-ийн радиус $r_D$, $\omega_{F'}$-ийн радиус $r_E$ гэе.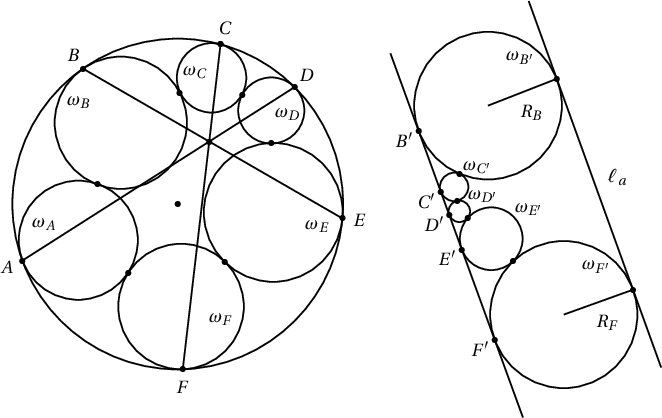 $BE\cap CF=M$. Одоо $B'E'A$, $C'F'A$ гурвалжнуудыг багтаасан тойргуудын огтлолцол $M'$-д бууна, $AD\to AD'$, мөн $AB$ нь $\Delta B'E'A$, $\Delta C'F'A$-г багтаасан тойргуудын радикал тэнхлэг тул $M'\in AD'$ буюу $C'D'\cdot D'F'=D'E'\cdot B'D'$ гэж батлахад хангалттай. $$C'D'=\sqrt{(r_C+r_D)^2-(r_C-r_D)^2}=2\sqrt{r_Cr_D}$$ төстэйгөөр $D'E'=2\sqrt{r_Dr_E}$, $E'F'=2\sqrt{Rr_E}$, $B'C'=2\sqrt{Rr_C}$ болно. Эндээс $$C'D'\cdot D'F'=2\sqrt{r_C\cdot r_D}\cdot(2\sqrt{r_D\cdot r_E}+2\sqrt{R\cdot r_E})$$ $$D'E'\cdot B'D'=2\sqrt{r_D\cdot r_E}\cdot(2\sqrt{r_C\cdot r_D}+2\sqrt{R\cdot r_C})$$ тул $C'D'\cdot D'F'=D'E'\cdot B'D'$ болно. Иймд $D'\in AM'$ болж $AD$, $BE$, $CD$-үүд 1 цэгт огтлолцоно.

Заавар.

Бодолт. Тэнцэтгэл бишийн 2 талыг $\sqrt{xyz}$-д хувааж, квадрат зэрэгт дэвшүүлбэл: $$\left(\dfrac{1}{x^2(1-x)+y^2(1-y)+z^2(1-z)}\right)^2\le\dfrac{1}{x(1-x)^2}+\dfrac{1}{y(1-y)^2}+\dfrac{1}{z(1-z)^2}$$ $f(x)=\dfrac{1}{x^2}$ функц авч үзье. $f''(x)=\dfrac{6}{x^4}>0$ тул $f(x)$ нь хотгор функц байна. Иймд $\alpha=x$, $\beta=y$, $\gamma=z$, $x_1=x(1-x)$, $x_2=y(1-y)$, $x_3=z(1-z)$ гээд Йенсений тэнцэтгэл биш бичвэл $$f(\alpha x_1+\beta x_2+\gamma x_3)\le \alpha f(x_1)+\beta f(x_2)+\gamma f(x_3)$$ буюу $$\dfrac{1}{\big(x^2(1-x)+y^2(1-y)+z^2(1-z)\big)^2}\le\dfrac{x}{x^2(1-x)^2}+\dfrac{y}{y^2(1-y)^2}+\dfrac{z}{z^2(1-z)^2}$$ болж тэнцэтгэл биш батлагдав.

Заавар.

Бодолт. $\angle YB_1C$-ийн биссектрисс $AY$-тэй $E$ цэгээр, $\angle YC_1B$-ийн биссектрисс $AY$-тэй $F$-цэгээр огтлолцдог байг. $(C_1B_1)\cap(CB)=P$ гэе. $BB_1$, $CC_1$, $AA_1$ нь чевианууд ба $P\in(C_1B_1)$, $P\in(BC)$ тул $(P, C, A_1, B)$ нь гармоник дөрвөл болно. Эндээс $(P, B_1, X, C_1)$ нь мөн гармоник дөрвөл болно. $(*)$

$\angle XYP=90^\circ$ мөн $(*)$-оос гармоник тухай 2-р теоремоос $\angle C_1YX=\angle XYB_1$ болно. Мөн $\angle C_1AX=\angle XAB_1$ тул биссектриссийн чанар ёсоор $$\dfrac{C_1Y}{B_1Y}=\dfrac{C_1X}{B_1X},\quad\dfrac{AC_1}{AB_1}=\dfrac{C_1X}{B_1X}\Rightarrow\dfrac{AC_1}{C_1Y}=\dfrac{AB_1}{B_1Y}\qquad(**)$$

$B_1E$ нь $\Delta AB_1Y$-ийн гадаад өнцгийн биссектрисс тул биссектриссийн чанараар $\dfrac{AB_1}{B_1Y}=\dfrac{AE}{EY},\quad(1)$;

$C_1F$ нь $\Delta AC_1Y$-ийн гадаад өнцгийн биссектрисс тул $\dfrac{AC_1}{C_1Y}=\dfrac{AF}{FY},\quad(2)$.

$(**)$, $(1)$, $(2)$-оос $E\equiv F$ гэж гарах ба $E\in(AY)$ ба $F\in(AY)$ тул $Z\equiv E\equiv F$ болж батлах зүйл батлагдав.

Заавар.

Бодолт. Лемм. $2 < p\in\mathbb P$ байг.

(i) $\alpha\ge1$ бол $p^\alpha\mid a+1\Longleftrightarrow p^{\alpha+1}\mid a^p+1$. Эндээс $\forall a\in\mathbb N$-ийн хувьд $p^2\mathop{\not\bigg|}\dfrac{a^p+1}{a+1}$.

(ii) $a\ge 4$ үед $\exists q\in\mathbb P\colon q\mathop{\bigg|}\dfrac{a^p+1}{a+1}$ ба $q\nmid a+1$ байна.

(i)-г баталъя. $a\equiv -1\pmod{p^\alpha}$ гэе. $a\equiv-1\pmod{p}$ тул $a^{p-1}-a^{p-2}+\cdots+1\equiv p\equiv 0\pmod{p}$ болно. $a^p+1=(a+1)(a^{p-1}-a^{p-2}+\cdots+1)$ гэдгээс $p^{\alpha+1}\mid a^p+1$ болно.

$a^p\equiv -1\pmod{p^{\alpha+1}}$ гэе. $a^p\equiv a\equiv1\pmod{p}$ тул $a=pk-1$ болно. Иймд \begin{align*} \dfrac{a^p+1}{a+1}&=(pk-1)^{p-1}-(pk-1)^{p-2}+\cdots+1\\ &\equiv\{-pk(p-1)+1\}-\{pk(p-2)-1\}+\cdots+1\\ &\equiv-pk\frac{p(p-1)}{2}+p\equiv p\pmod{p^2} \end{align*} болно. Өөрөөр хэлбэл $\textrm{ord}_p\big(\frac{a^p+1}{a+1}\big)=1$ байна. Иймд $p^{\alpha}\mid a+1$ ба $p^2\mathop{\not\bigg|}\dfrac{a^p+1}{a+1}$ байна.

(ii)-г баталъя. Эсрэгээс нь аливаа $q\mathop{\bigg|}\dfrac{a^p+1}{a+1}$-ийн хувьд $q\mid a+1$ гэвэл $a\equiv -1\pmod{q}$ тул $$a^{p-1}-a^{p-2}+\cdots+1\equiv p\equiv 0\pmod{q}.$$ Эндээс $q=p$ болно. Иймд $p^{\alpha}=\dfrac{a^p+1}{a+1}$. Гэтэл (i)-ээр $$p=\frac{a^{p}+1}{a+1}=a^{p-1}-a^{p-2}+\cdots+1>a^{p-1}-a^{p-2}=a^{p-2}(a-1)\ge 3\cdot 4^{p-2}$$ болж зөрчил үүсч байна.

Одоо $k$-аар индукцлэж байгуулъя. $k=1,2$ үед $2^{3^2}+1=27\cdot 19$ байна. Эндээс $\dfrac{2^{3^2}+1}{3^3}\in\mathbb N$ ба $$\frac{2^{3^2}+1}{3^3\cdot 19}\in\mathbb N\overset{\text{(i)}}{\Longrightarrow}\frac{2^{3^2\cdot 19}+1}{3^3\cdot 19^2}\in\mathbb N\overset{\text{(i)}}{\Longrightarrow}\frac{2^{3^2\cdot 19^2}+1}{3^3\cdot 19^3}\in\mathbb N$$ болно. $\dfrac{2^{(p_1\dots p_s)^2}+1}{(p_1\dots p_s)^3}\in\mathbb N$ байг. $a=2^{(p_1\dots p_{s-1})^2}$ гэе. (ii)-ээр $q\,\Big|\,\dfrac{a^{p_s^2}+1}{a+1}$ ба $q\nmid a+1$ байх $q$ олдоно. $p_1\dots p_{s-1}\mid a+1$ тул $(q, p_1\dots p_{s-1})=1$ байна. Нөгөө талаас $q=p_s$ гэвэл $p_s^3\mid a^{p_s^2}+1\overset{\text{(i)}}{\Longrightarrow}p_s^2\mid a^{p_s}+1\overset{\text{(i)}}{\Longrightarrow} q=p_s\mid a+1$ болж зөрчил. Иймд $(q,p_1\dots p_s)=1$ болох ба $$q\mid a^{p_s^2}+1\overset{\text{(i)}}{\Longrightarrow}q^2\mid a^{p_s^2\cdot q}+1\overset{\text{(i)}}{\Longrightarrow}q^3\mid a^{p_s^2q^2}+1$$ буюу $\dfrac{2^{(p_1\dots p_sq)^2}+1}{(p_1\dots p_sq)^3}\in\mathbb N$ болно.