Заавар.

Бодолт. Дурдсан чанартай $n$ шулуунаар хавтгай $V(n)$ хэсэгт хуваагддаг гэж тэмдэглэе. $V(k+1)=V(k)+k+1$, $V(1)=2$ гэсэн рекурент харьцаа биелэхийг баталъя. $k$ шулуун татагдсан байг. $k+1$-р шулууныг авч үзэхэд тэр нь бусадтайгаа $k$ цэгээр огтлолцож $k+1$ хэсэгт хуваагдана. Энэхүү хэсэг бүр нь хавтгайн ямар нэг хуучин хэсгийг 2 хуваах тул $V(k+1)=V(k)+k+1$ боллоо. Иймд $$V(n)=2+(2+3+\dots+n)=\dfrac{n^2+n+2}{2}$$

Заавар.

Бодолт. $a_ib_j$ хэлбэрийн $n^2$ тоог $n\times n$ торонд дураараа байрлуулсан байг. $S$ нь анхны хүснэгтэд буй бүх $1$ ба $-1$-үүдийн нийлбэр бол $S>0$ болно. \begin{align*} \sum a_ib_j&=a_1(b_1+\dots+b_n)+a_2(b_1+b_2+\dots+b_n)+\dots+a_n(b_1+\dots+b_n)\\ &=(a_1+a_2+\dots+a_n)(b_1+b_2+\dots+b_n)=S^2>0 \end{align*} Одоо мөрүүдийн хооронд дараах байдлаар цикл гэж нэрлэгдэх шилжилт хийе. 1 мөрийг $n$-р мөрд шилжүүлж бусад мөрүүдийг эрэмбээр нь дээш нь шилжүүлье. Дараа нь гарсан хүснэгтэд энэ процессыг давтана гэх мэтээр цааш үргэлжлүүлье. Ингэхэд 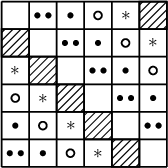зураг дахь байдал ажиглагдана. Энд I шилжилтээр зурагдсан хүснэгтэд буй тоонууд диагональд шилжиж байхад, II шилжилтээр $*$-тэй хүснэгтийн тоонууд диагональд шилжих болно, гэх мэтээр цааш үргэлжлүүлнэ. Хэрэв анх дурдсан диагоналийн дагуу тоонууд сөрөг биш байсан бол бодлого бодогдсон хэрэг. Эсрэг тохиолд саяын шинээр диагональд гарах тоонуудын нийлбэр ямагт эерэг биш байдаг бол тэдний нийлбэр $\sum a_ib_j$-тэй тэнцэх тул $\sum a_ib_j$ болж зөрчил үүснэ. Иймд ядаж нэг цикл шилжилтээр тус диагоналийн дагуу эерэг тоо гарна.

Заавар.

Бодолт. Эсрэгээс нь манай дүрсийн тэгш хэмийн тэнхлэгүүд нь нэг цэгт огтлолцдоггүй гэж үзвэл тийм гурван тэнхлэг $\ell_1, \ell_2, \ell_3$ олдоно. Манай дүрсийн аль ч хоёр тэнхлэг параллель байж чадахгүй. Учир нь тэр хоёр тэнхлэгийн хувьд дараалан хийсэн хувиргалтаар манай дүрс параллелиар зөөгдөнө. Гэтэл ямар ч төгсгөллөг дүрс параллель зөөлтөөр өөртэйгөө давхацдаггүй. 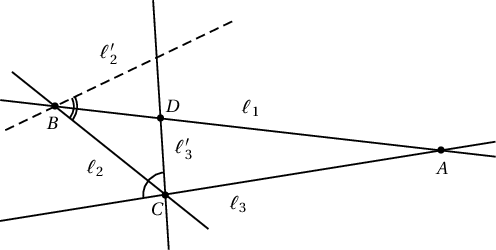Учир нь $\ell_2, \ell'_2, \ell_3$ тэнхлэгүүдийг авч үзвэл $\angle(\ell_2,\ell_2)=2\cdot\angle B$ болох ба $\ell'_2$ нь мөн л манай дүрсийн тэгш хэмийн тэнхлэг билээ. Энд $\ell'_2$ нь $\ell_1$-ийн хувьд $\ell_2$-тай тэгш хэмтэй орших шулуун. Мөн $\triangle ABC$ нь хамгийн бага талбайтай мохоо өнцөгтэй гурвалжин гэж үзэж чадна. Учир нь төгсгөлөг тооны тэнхлэгүүдийн огтлолцолд нийт төгсгөлөг тооны гурвалжин үүссэн байгаа. $\ell_2$-ийн хувьд $\ell_3$-тэй тэгш хэмтэй орших шулуун нь $\ell'_3$ гэвэл $\ell'_3\perp\ell_1$ болно. Эс тэгвэл $\triangle ABC$-ийн сонголтод харшилна. $|AD| < |DB|$ бол $\ell'_3$-ийн хувьд $\ell_3$-тэй тэгш хэмтэй орших $\ell''_3$ тэнхлэг ба $\ell_1$, $\ell_2$-ийн огтлолцолд $\triangle ABC$-ээс бага талбайтай мохоо өнцөгт гурвалжин үүсэхэд хүрэх тул $\triangle ABC$ нь адил хажуут байна. Тэгвэл $\ell'_2\parallel \ell_3$ болж зөрчилд хүрнэ.

Заавар.

Бодолт. $\angle A=\alpha$, $\angle B=\beta$, $\angle C=\gamma$ гэе. 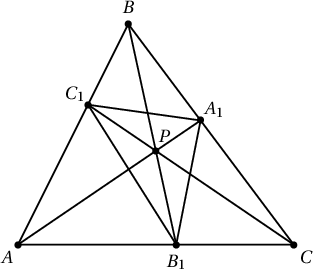Өгөгдсөнөөр $$\dfrac{AB_1}{B_1C}=\mu,\quad\dfrac{CA_1}{A_1B}=\nu,\quad\dfrac{BC_1}{C_1A}=\chi$$ ба Чевийн теоремоор $\mu\nu\chi=1$ байна. Түүнчлэн $$S_{A_1B_1C_1}=S-S_{AB_1C_1}-S_{BC_1A_1}-S_{CA_1B_1}\qquad(1)$$ Одоо $S_{AB_1C_1}$, $S_{BC_1A_1}$, $S_{CA_1B_1}$-үүдийг олъё. $$S_{AB_1C_1}=\dfrac{1}{2}\cdot AB_1\cdot AC_1\sin\alpha$$ $$S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\sin\alpha$$ ба $$AB_1=\dfrac{\mu}{\mu+1}AC,\quad AC_1=\dfrac{1}{\chi+1} AB$$ тул $$S_{AB_1C_1}=\dfrac{\mu}{(1+\mu)(1+\chi)}\cdot S_{ABC}\qquad(2)$$ ба үүний адилаар $$S_{CA_1B_1}=\dfrac{\nu}{(1+\nu)(1+\mu)}\cdot S_{ABC}\qquad(3)$$ $$S_{BA_1C_1}=\dfrac{\chi}{(1+\chi)(1+\nu)}\cdot S_{ABC}\qquad(4)$$ болно. $(1)$--$(4)$-ээс \begin{align*} S_{A_1B_1C_1}&=\left(1-\dfrac{\mu}{(1+\mu)(1+\chi)}-\dfrac{\nu}{(1+\nu)(1+\mu)}-\dfrac{\chi}{(1+\chi)(1+\nu)}\right)S\\ &=\dfrac{(1+\mu\nu\chi)S}{(1+\mu)(1+\nu)(1+\chi)}=\dfrac{2S}{(1+\mu)(1+\nu)(1+\chi)} \end{align*} тул $(1+\mu)(1+\nu)(1+\chi)$ хамгийн бага үед $S_{A_1B_1C_1}$ хамгийн их байна. Кошийн тэнцэтгэл бишээр $$(1+\mu)(1+\nu)(1+\chi)\ge 2\sqrt{1\cdot \mu}\cdot 2\sqrt{1\cdot \nu}\cdot 2\sqrt{1\cdot \chi}=8\sqrt{\mu\nu\chi}=8$$ ба $$\mu=\nu=\chi=1$$ үед тэнцэлдээ хүрнэ. Иймд $P$ цэг хүндийн төв үед $$S_{A_1B_1C_1}=\dfrac{2S}{8}=\dfrac{S}{4}$$ хамгийн их утгатай байна.

Заавар.

Бодолт. $1977=a_1+a_2+\dots+a_n+p$ гэж бичсэн бөгөөд энд $n$ нь манай олбол зохих тоо гэж сэтгэвэл бодлогын нөхцөл ёсоор $a_i\ge 10$ байж үл болно. Үнэхээр, $a_i\ge 10$ бол $a_i=ab$ ба $a\ge 2$, $b\ge 4$ гэж үзэж ямагт болно. Иймд $b\ge 4$ байх $b$ тоог $b=c+d$, $c>1$, $d>1$ дүрстэй бичиж болох тул $$a_i=a(c+d)=ac+ad$$ болж $1977$-г $n+1$ ширхэг зохиомол тоо болон $1$ ширхэг анхны тооны нийлбэрээр бичихэд хүрнэ. Иймд $a_i\le 9$ байна. Мөн дээрхийн адилаар $a_i=8$ байж болохгүй. Учир нь $8=4+4$ ба $4$ нь зохиомол тоо билээ. Иймд $a_i$ нь $4,6,9$ гэсэн утгатай л байж болно. Учир нь $$6+6=12=4+4+4$$ гэж бичвэл дээрх $a_i=6$ ба $a_j=6$-ийн оронд $a_i=4$, $a_j=4$, $a_{n+1}=4$ гэж авч болох учраас $1977$-г $n+1$ ширхэг зохиомол тоо ба $1$ ширхэг анхны тооны нийлбэр дүрстэй бичиж болоход хүрч байна.

Харин $$1977=4+\dots+4+5=4\cdot 493+5$$ гэж бичиж болно. Үүнээс өөрөөр бичлэг байх болбол түүнд $6$ ба $9$ нэг нэг удаа бусад нь дан $4$ эсвэл, $6$, $9$ зэрэг орсон бусад нь дан $4$ гэсэн байдлаар бичигдэж болно. Өөрөөр хэлбэл $$1977=4+\dots+4+6+p_1$$ $$1977=4+\dots+4+9+p_2$$ $$1977=4+\dots+4+6+9+p_3$$ дүрстэй байх боломжтой. Энд $p_1$, $p_2$, $p_3$ тохирох анхны тоо.

Одоо $p_i>5$ байж болохгүйг харуулъя. Хэрэв $p_i=2k+1$, $k\ge 3$ бол $p'_i=3$ гэж аваад үлдсэн $k-1\ge 2$ ширхэг $2$-ыг нь харгалзах нэмэгдэхүүн $4$-үүд дээр нэмж $6+6$-г ямагт гаргаж болох учраас энэ нь бодлогын нөхцөлд мөн зөрчинө. Иймд $$1977=4+\dots+4+6+3$$ $$1977=4+\dots+4+5$$ гэсэн хоёрхон бичлэг л байж болох нь харагдана.

Заавар.

Бодолт. Тойрог дээр өгөгдсөн $n$ цэгүүдийг дараалан холбоход гүдгэр $n$ өнцөгт үүснэ. Энэ $n$ өнцөгтийн диагоналиудыг татахад тэдний аль ч 3 нь нэг цэгт үл огтлолцох ба дурын 4-ийг сонгон авч эдгээр оройг холбогч диагоналиудыг татахад зөвхөн нэг л огтлолцлын цэг олдох нь илэрхий. Иймд бүх диагоналиудын огтлолцлын цэгийн тоо $C_n^4$ болно. Эдгээр диагоналиудыг татахад $n$ өнцөгт нь гурвалжин, дөрвөн өнцөгт, 5 өнцөгт гэхчлэн $m$ өнцөгтүүдэд хуваагдсан ба тэдний тоо харгалзан $N_3,N_4,\dots,N_M$ гэвэл энэ $n$ өнцөгт бүгд $$N_3+N_4+\dots+N_m$$ мужид хуваагдана. Иймд олбол зохих мужийн тоо $$m+N_3+N_4+\dots+N_m$$ байх нь илэрхий. Одоо $N=N_3+N_4+\dots+N_m$-ийг олъё. Бүх олон өнцөгтийн оройнуудын тоо давталтын хамтаар $3N_3+\dots+mN_n$ байна. Гэтэл диагоналийн огтлолцлын цэг бүр $4$ дүрсийн орой болно. Иймд $4$ дүрсийн орой болох цэгүүд давталтын хамт $4\cdot C_n^4$ байна. Өгөгдсөн $n$ цэг тус бүр $n-$ гурвалжны орой болно. Тийм бүх гурвалжны оройн тоо нь давхардалтайгаар $n(n-2)$ ширхэг байна. Иймд $$3N_3+\dots+mN_n=4C_n^4+n(n-2)\qquad(1)$$ болно. Одоо эдгээр бүх олон өнцөгтүүдийн дотоод өнцгүүдийн нийлбэрийг олъё. Бүx гурвалжнууд, дөрвөн өнцөгтүүд гэx мэт $m$-өнцөгтүүдийн дотоод өнцгүүдийн нийлбэр нь тус тусдаа $$\pi N_3, 2\pi N_4, \ldots, (m-2)\pi N_m$$ байна. 4 өнцөгт бүр нь диагоналийнхаа огтлолцлын цэгээр нэг утгатай тодорхойлогдох учраас $$\pi N_3+2\pi N_4+\dots+(m-2)\pi N_m=2\pi C_n^4+(n-2)\pi$$ болно.

Учир нь диагоналийн огтлолцлын цэг бүрд $2\pi$ өнцөг харгалзах ба уг олон өнцөгтийн дотоод өнцөг нь $(n-2)\pi$. Тэгвэл $$N_3+2N_4+\dots+(m-2)N_m=2C_n^4+(n-2)\qquad(2)$$ боллоо. $(1$) ба $(2)$-оос $$N_3+N_4+\dots+N_m=C_n^4+\dfrac{(n-2)(n-1)}{2}$$ болох тул нийт хуваагдах мужийн тоо нь $$n+C_n^4+\dfrac{(n-1)(n-2)}{2}$$ боллоо.