Заавар.

Бодолт. $AB=c$, $BC=a$, $AC=b$, $AA_1=h_1$, $BB_1=h_2$, $CC_1=h_3$, $AO=h'_1$, $BO=h'_2$, $CO=h'_3$ гэж тэмдэглэе. 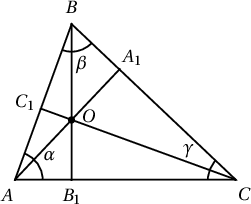$SR=\dfrac{abc}{4}$ болох нь синусын теоремоос шууд гаргана. Иймд батлах тэнцэл маань $$\dfrac{ch'_1h'_2}{4}+\dfrac{ah'_2h'_3}{4}+\dfrac{bh'_1h'_3}{4}=\dfrac{abc}{4}$$ буюу $$\dfrac{h'_1h'_2}{ab}+\dfrac{h'_2h'_3}{bc}+\dfrac{h'_1h'_3}{ac}=1$$ болно. $\angle BOA=\pi-\gamma$ болох нь илэрхий тул \begin{align*} \dfrac{h'_1h'_2}{ab}+\dfrac{h'_2h'_3}{bc}+\dfrac{h'_1h'_3}{ac}&=\dfrac{h'_1h'_2\sin(\pi-\gamma)}{ab\sin\gamma}+\dfrac{h'_2h'_3\sin(\pi-\alpha)}{bc\sin\alpha}+\dfrac{h'_1h'_3\sin(\pi-\beta)}{ac\sin\beta}\\ &=\dfrac{S_C}{S}+\dfrac{S_A}{S}+\dfrac{S_B}{S}=\dfrac{S}{S}=1 \end{align*}

Заавар.

Бодолт. Зургаатын тооллын системд манай $n$ оронтой тоо нь $1\le a_i\le 5$, $$\overline{a_0\ldots a_{n-1}}=a_0+a_1\cdot 6+\dots+a_{n-1}\cdot 6^{n-1}$$ гэж бичигдэнэ. Ийм тооны нийт тоо нь $5^n$ байх ба тодорхойлон бэхэлсэн $a_i$ цифр нь $5^{n-1}$ удаа давтагдана. Учир нь $a_i$-ийг бэхэлсэн үед $a_0,\ldots,a_{i-1},a_{i+1},\ldots,a_n$-үүд нь тус бүр 5 янзын утгыг дураараа авч болох тул тэднийг сонгох боломж нь $5^{n-1}$ байна. Иймд \begin{align*} \sum\overline{a_0\ldots a_{n-1}}&=5^{n-1}\{(1+2+\dots+5)+(1+2+\dots+5)\cdot 6+\dots+(1+2+\dots+5)6^{n-1}\}\\ &=5^{n-1}\cdot 15\cdot\dfrac{6^n-1}{6-1}=5^{n-1}\cdot 3\cdot (6^n-1) \end{align*}

Заавар.

Бодолт. Аль ч гурав нь нэг шулуун дээр үл орших 6 цэгийн хувьд дурдсан гурвалжин ямагт оршихыг баталъя. Хэрэв уг 6 цэг гүдгэр 6 өнцөгтийн орой дээр оршвол уг 6 өнцөгтийн ядаж нэг өнцөг нь $120^\circ$-аас багагүй байх нь илэрхий. Хэрэв уг 6 цэгийг агуулсан гүдгэр олонлог 5 өнцөгт бол 6 дахь цэг нь энэ 5 өнцөгтийн дотор орших тул түүнийг аль нэг 3 цэгээр нь тодорхойлогдох гурвалжны дотор байна гэж үзэж болно. Энэ тохиолдолд уг цэгийг гурвалжны 3 оройтой холбоход заавал дурдсан чанар бүхий гурвалжин олдоно. Хэрэв уг 6 цэгийг агуулсан гүдгэр олонлог нь дөрвөн өнцөгт эсвэл гурвалжин бол мөн адилаар бодогдоно. Иймд $C_n^6$ дурдсан гурвалжин олдох нь илэрхий. Гэтэл үүний нэг гурвалжин нь 3 цэгээрээ тодорхойлогдох ба үлдэх гурван цэгийг $C_{n-3}^3$ янзаар сонгох ба уг гурвалжин нийт $C_{n-3}^3$ удаа давтагдан тоологдох тул нийт гурвалжны тоо $\dfrac{C_n^6}{C_{n-3}^3}$ байна.

Заавар.

Бодолт. $$\dfrac{k+x_1}{x_1}=\dfrac{k+x_1}{x_2}+1\Rightarrow \dfrac{k}{x_1}=\dfrac{k+x_1}{x_2}\Rightarrow x_2=\dfrac{k+x_1}{k}\cdot x_1$$ байна. Индукцээр $$x_s=\left(\dfrac{k+x_1}{k}\right)^{s-1}\cdot x_1$$ болохыг баталъя. $s < t$ үед үнэн гээд $s=t$ үед баталъя. $$\dfrac{k+x_1+\dots+x_{t-1}}{x_{t-1}}=\dfrac{k+x_1+\dots+x_t}{x_t}\Rightarrow$$ $$\dfrac{k+x_1+\dots+x_{t-2}}{x_{t-1}}=\dfrac{k+x_1+\dots+x_{t-1}}{x_t}\Rightarrow$$ \begin{align*} x_t&=\dfrac{k+x_1+\dots+x_{t-1}}{k+x_1+\dots+x_{t-2}}\cdot x_{t-1}\\ &=\dfrac{k+x_1+\dots+x_{t-1}}{k+x_1+\dots+x_{t-3}}\cdot x_{t-2}\\ &\qquad\qquad\qquad\vdots\\ &=\dfrac{k+x_1+\dots+x_{t-1}}{k}\cdot x_{1}\\ \end{align*} Нөгөө талаас \begin{align*} x_1+x_2+\dots+x_{t-1}&=\sum_{s=1}^{t-1}\left(\dfrac{k+x_1}{k}\right)^{s-1}\cdot x_1\\ &=\dfrac{x_1\left(\left(\dfrac{k+x_1}{k}\right)^{t-1}-1\right)}{\dfrac{k+x_1}{k}-1}\\ &=k\cdot\left(\dfrac{k+x_1}{k}\right)^{t-1}-k \end{align*} тул $$x_t=\left(\dfrac{k+x_1}{k}\right)^{t-1}\cdot x_1$$ болж батлагдав.

$x_1+\dots+x_n=k$ гэдгээс $$k\cdot\left(\dfrac{k+x_1}{k}\right)^{n}-k=k\Rightarrow \left(\dfrac{k+x_1}{k}\right)^{n}=2$$ болно. Иймд $x_1=k(\sqrt[n]{2}-1)$ ба $\dfrac{k+x_1}{k}=\sqrt[n]{2}$ тул $x_s=k(\sqrt[n]{2}-1)\sqrt[n]{2^{s-1}}$, $s=\overline{1,n}$ байна.

Заавар.

Бодолт. $O$ нь тойргийн төв ба $XY$ хөвчид перпендикуляр радиусын хувьд $M$ цэгтэй тэгш хэмтэй орших цэг нь $M'$ бол $OM=OM'$ байна. $\rho=OA$ ба $r$ нь өгөгдсөн тойргийн радиус байг. 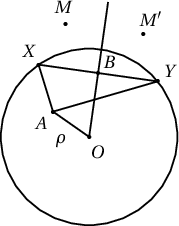Одоо $OM'=\sqrt{2r^2-\rho^2}$ болохыг баталъя. Өөрөөр хэлбэл $OM'$ нь $XY$ хөвчийн байрлалаас үл хамаарахыг баталъя.

$A$ цэгийг тэнхлэгийн тэгш хэмээр 2 удаа дараалан хувиргахад $M'$ цэг гарлаа гэж үзэж болох тул $M'$ нь $XY$ хөвчийн дундаж цэг $b$-ийн хувьд $A$-тай тэгш хэмтэй орших тул $AXM'Y$ нь тэгш өнцөгт болно. Учир нь $AXM'Y$ нь нэг тэгш өнцөгт бүхий параллелограмм болсон байгаа.

Лемм. $ABC$ гурвалжинд $AD=DB$, $CD$-үүд нь тогтмол бол $AC^2+CB^2$ нь мөн тогтмол байна.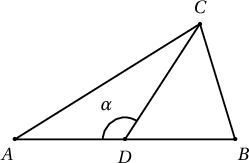 Баталгаа. Косинусын теоремоор $$AC^2=AD^2+DC^2-2AD\cdot DC\cdot \cos{\alpha}$$ $$CB^2=DB^2+DC^2-2DB\cdot DC\cos{(180^\circ-\alpha)}$$ тул ба $\cos(180^\circ-\alpha)=\cos\alpha$, $DB=AD$ тул дээрх хоёр илэрхийллийг нэмэхэд $$AC^2+CB^2=2AD^2+2DC^2$$ болж лемм батлагдав.

Иймд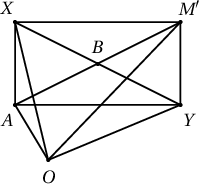 $$AO^2+OM'^2=2AB^2+2BO^2,$$ $$OX^2+OY^2=2XB^2+2BO^2$$ болох ба энд $AB=XB$ байгааг анхаарч үзвэл $AO^2+OM'^2=OX^2+OY^2$ гэж гарна. Эндээс $$OM'^2=OX^2+OY^2-AO^2=2r^2-\rho^2$$ буюу $OM'=\sqrt{2r^2-\rho^2}$. Иймд тийм $M$ цэгийн геометр байр нь $O$ дээр төвтэй $OM=\sqrt{2r^2-\rho^2}$ радиустай тойрог болно.

Жич: Энд дээрх тойргийн цэг бүр ямар нэг $XY$ хөвчид харгалзан гэдгийг харуулах шаардлагатай.

Заавар.

Бодолт. $a=\overline{a_1\dots a_n}$ нь олбол зохих тоо байг. $$S(a)=\sum_{i=1}^n a_1+\sum_{i < j} a_i a_j+\cdots +a_1 \cdots a_n$$ гэж тэмдэглэе. \begin{align*} S(a)&=\prod_{i=1}^n (1+a_1)-1=a_1\prod_{i=2}^n (1+a_i)+\prod_{i=2}^n(1+a_i)-1\\ &=\cdots\\ &=a_1\prod_{i=2}^n (1+a_i)+a_2\prod_{i=3}^n (1+a_i)+\cdots+a_n+1-1\\ &\le a_1\cdot 10^{n-1}+a_2\cdot 10^{n-2}+\cdots +a_n=\overline{a_1\cdots a_n}=a \end{align*} тул $S(a)=a$ байхын тулд $i\ge 2$ үед $1+a_i=10$ байх ёстой болов. Өөрөөр хэлбэл, $\overline{a_1 9\cdots 9,}$ $a_1 =1,2,\dots 9$ хэлбэрийн тоонуудаас өөр тоо манай бодлогын шийд болж үл чадна.