ММО-18, 10-р анги
Бодлогын тоо: 6 Хугацаа: 540 мин
1. $4^{18}+4^{1000}+4^n$ тоог бүтэн квадрат байлгах хамгийн их натурал тоо $n$-ийг ол.
Заавар Бодолт
Заавар.
Бодолт. $4^{18}+4^{1000}+4^{n}=4^{18}(1+4^{982}+4^{n-18})$ бүтэн квадрат байхын тулд $1+4^{982}+4^{n-18}=a^2,\quad a\in \mathbb{Z} $ байх ёстой. $$1+4^{982}+4^{s}=1+2\cdot 2^{1963}+2^{2s},\quad s=1963$$
буюу $n=1981$ үед энэ тоо бүтэн квадрат болно.
Одоо $s$ нь $1963$-аас их бол шийд болохгүйг үзүүлье. Эсрэгээр $1+2^{1964}+2^{2s}=a^2,\quad s>1963$ болог. Тэгвэл $$2^{2s} < a^2 = 2^{2s} +2\cdot 2^{1963}+1 < 2^{2s}+2\cdot 2^s+1=(2^{2s}+1)^2$$ буюу $$2^{2s} < a < 2^{2s}+1$$ болж зөрчилд хүрэв. Иймд хамгийн их $n$ тоо нь $1981$ болов.
Одоо $s$ нь $1963$-аас их бол шийд болохгүйг үзүүлье. Эсрэгээр $1+2^{1964}+2^{2s}=a^2,\quad s>1963$ болог. Тэгвэл $$2^{2s} < a^2 = 2^{2s} +2\cdot 2^{1963}+1 < 2^{2s}+2\cdot 2^s+1=(2^{2s}+1)^2$$ буюу $$2^{2s} < a < 2^{2s}+1$$ болж зөрчилд хүрэв. Иймд хамгийн их $n$ тоо нь $1981$ болов.
2. Тал тус бүрийн урт ба аль нэг зэрэгцээ хоёр өнцгийнх нийлбэр өгөгдсөн 4 өнцөгтийг байгуул.
Заавар Бодолт
Заавар.
Бодолт. $ABCD$ нь байгуулбал зохих дөрвөн өнцөгт байг.
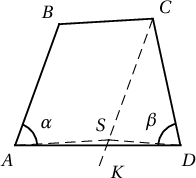$\angle BAD=\alpha$, $\angle CDA=\beta$ гэе. $AB\parallel CK$-г татаж $|AB|=|CS|$ байх $S$ цэгийг $CK$ шулуун дээр авъя. $\angle KCD=\pi-(\alpha+\beta)$ болох ба $ABCS$ нь параллелограмм юм. Эндээс $ABCD$ байгуулахын тулд $ASCD$-г байгуулбал хүрэлцээтэй гэж гарна.
$ASCD$-г байгуулахдаа $\triangle SCD$-г өгсөн 2 тал $|SC|=|AB|$, $|CD|$ ба хоорондох өнцөг $\angle SCD=\pi-(\alpha+\beta)$-ээр байгуулж $S$ цэг дээр төвтэй $|AS|=|BC|$ радиустай тойрог, $D$ цэг дээр төвтэй $|AD|$-радиустай тойргуудын огтлолцлын цэг нь $A$ орой болно. Ингэж $ASCD$ дөрвөн өнцөгтийг байгуулна.
$ASCD$-г байгуулахдаа $\triangle SCD$-г өгсөн 2 тал $|SC|=|AB|$, $|CD|$ ба хоорондох өнцөг $\angle SCD=\pi-(\alpha+\beta)$-ээр байгуулж $S$ цэг дээр төвтэй $|AS|=|BC|$ радиустай тойрог, $D$ цэг дээр төвтэй $|AD|$-радиустай тойргуудын огтлолцлын цэг нь $A$ орой болно. Ингэж $ASCD$ дөрвөн өнцөгтийг байгуулна.
3. Тус бүр нь 1 кг-аас хэтрэхгүй хэсэг чулууны нийт жин 20 кг-аас үл хэтэрнэ. 3 кг даацтай жинлүүрээр хамгийн цөөндөө хэчнээн удаа жинлэж нийт чулууны жинг мэдэж болох вэ?
Заавар Бодолт
Заавар.
Бодолт. $1\ge a \ge \dfrac{20}{27}$ кг жинтэй чулууны тоог $S(a)$ гэж тэмдэглэе. Тэгвэл $S(a)\le 27$ байна. Эдгээрийг гурав гурваар нь 9 жинлэе. Тэдгээрийн жинг харгалзан $m_1,m_2,\cdots ,m_9$ гэе. Хэрэв бүх чулуу тэдгээрт орж байвал жинлэлт дуусна.
$b<\dfrac{20}{27}$ кг жинтэй чулуу оршин байг. Тэгвэл $\min m_i\le \dfrac{20-b}{9}<3-b$ учир $m_i$ дээр тавьж жинлэнэ.
Одоо $8$ жинлэлт хангалтгүйг үзүүлье. $\dfrac{4}{5}$ кг жинтэй $25$ ширхэг чулууны нийт жин $20$ кг байна. $1$ жинлэлтээр $3$-аас олныг жинлэж үл чадна. $\dfrac{4}{5}\cdot 4>3$ тул гурав гурваар нь $8$ удаа жинлэе. Гэтэл $1$ чулуу үлдэнэ. Иймд хамгийн цөөндөө гарцаагүй хийгдэх жинлэлтийн тоо $9$ байна.
$b<\dfrac{20}{27}$ кг жинтэй чулуу оршин байг. Тэгвэл $\min m_i\le \dfrac{20-b}{9}<3-b$ учир $m_i$ дээр тавьж жинлэнэ.
Одоо $8$ жинлэлт хангалтгүйг үзүүлье. $\dfrac{4}{5}$ кг жинтэй $25$ ширхэг чулууны нийт жин $20$ кг байна. $1$ жинлэлтээр $3$-аас олныг жинлэж үл чадна. $\dfrac{4}{5}\cdot 4>3$ тул гурав гурваар нь $8$ удаа жинлэе. Гэтэл $1$ чулуу үлдэнэ. Иймд хамгийн цөөндөө гарцаагүй хийгдэх жинлэлтийн тоо $9$ байна.
4. Дурын натурал тоо $n$ бүрийн хувьд $1982^n$ ба $1982^n+2^n$ тоонууд адил оронтой гэж батал.
Заавар Бодолт
Заавар.
Бодолт. Эсрэгээс нь $1982^n+2^n$ тооны орон $1982^n$ тооны оронгоос их байх $n$ гэсэн тоо олддог байг. Тэгвэл ямар нэг $k$ тоо олдоод $1982^n<10^k$, $1982^n+2^n\ge 10^k$ байна. $1982^n>10^{3n}$ учир $k>3n$ байна. Энэ тэнцэтгэл бишийн $2$ тал $2^n$-д бүхлээр хуваагдана.
$ \left\{ \begin{array}{l} 991^n<5^k\cdot 2^{k-n}\\ 991^n+1\ge 5^k\cdot 2^{k-n}\\ \end{array} \right.$ тэнцэтгэл бишийн системээс $991^n+1= 5^k\cdot 2^{k-n}$ болно. Гэтэл энэ тэнцэл шийдгүй. Учир нь тэнцлийн баруун гар тал нь ямагт $2$-оор, зүүн гар тал нь ямагт $0$-ээр төгсөнө. Ингэж зөрчилд хүрч дурын $n$-ын хувьд $1982^n+2^n$ ба $1982^n$ тоонууд адил оронтой байх нь батлагдав.
$ \left\{ \begin{array}{l} 991^n<5^k\cdot 2^{k-n}\\ 991^n+1\ge 5^k\cdot 2^{k-n}\\ \end{array} \right.$ тэнцэтгэл бишийн системээс $991^n+1= 5^k\cdot 2^{k-n}$ болно. Гэтэл энэ тэнцэл шийдгүй. Учир нь тэнцлийн баруун гар тал нь ямагт $2$-оор, зүүн гар тал нь ямагт $0$-ээр төгсөнө. Ингэж зөрчилд хүрч дурын $n$-ын хувьд $1982^n+2^n$ ба $1982^n$ тоонууд адил оронтой байх нь батлагдав.
5. Тоо бичсэн цаасны толгойг уруу нь харуулбал $0$, $8$, $1$ гэсэн цифрүүд үл өөрчлөгдөх ба $6$, $9$ гэсэн цифрүүд бие биедээ шилжиж бусад цифрүүд утгагүй тэмдэг болон хувирна. Цаасны толгойг уруу нь харуулахад үл өөрчлөгдөх бүх $n$ оронтой тоонуудын тоог ол.
Заавар Бодолт
Заавар.
Бодолт. Уг тоо $\overline{a_1{a_2}...{a_n}}$ хэлбэртэй байг. Тэгвэл энэ тоо $0$, $1$, $6$, $8$, $9$ цифрүүдэд бичигдэнэ. Энэ тоог дундуур нь $2$ тэнцүү хэсэгт салгая. Тэгвэл сүүлийн хэсгийн тоо урдах хэсгийн тоотой нэг ижил утгаар тодорхойлогдоно. Учир нь цаасны толгойг эргүүлсний дараа сүүлийн хэсгийн тоо нь урдах хэсгийн тоо болно. Иймд эдгээр тоонуудын тоотой тэнцүү.
$1)$ $n$ тэгш байг. Эхний хэсэгт $\dfrac{n}{2}$ цифр орно. $0$, $1$, $6$, $8$, $9$ цифрүүдээр зохиогдсон $\dfrac{n}{2}$ оронтой тоо $4\cdot{5^{\frac{n}{2}-1}}$ байна. Учир нь эхний цифр нь $0$ байж болохгүй бусад цифрийг дураараа сонгон авна.
$2)$ $n$ сондгой байг. Тэгвэл $2$ хэсэгт хуваахад голд 1 цифр үлдэнэ. Энэ нь урвуу харуулахад үл өөрчлөгдөх тул $0$, $1$, $8$ цифрийн нэг байна. Эдгээр тоонуудын тоо $12\cdot{5^{\frac{n-1}{2}-1}}$ байна.
$1)$ $n$ тэгш байг. Эхний хэсэгт $\dfrac{n}{2}$ цифр орно. $0$, $1$, $6$, $8$, $9$ цифрүүдээр зохиогдсон $\dfrac{n}{2}$ оронтой тоо $4\cdot{5^{\frac{n}{2}-1}}$ байна. Учир нь эхний цифр нь $0$ байж болохгүй бусад цифрийг дураараа сонгон авна.
$2)$ $n$ сондгой байг. Тэгвэл $2$ хэсэгт хуваахад голд 1 цифр үлдэнэ. Энэ нь урвуу харуулахад үл өөрчлөгдөх тул $0$, $1$, $8$ цифрийн нэг байна. Эдгээр тоонуудын тоо $12\cdot{5^{\frac{n-1}{2}-1}}$ байна.
6. Тэгшитгэлийг бод.
$$\left\{
\begin{array}{l}
\tg x_1+\ctg x_1=3\tg x_2\\
\tg x_2+\ctg x_2=3\tg x_3\\
\cdots\cdots\cdots\cdots\cdots\cdots\cdots\\
\tg x_n+\ctg x_n=3\tg x_1
\end{array}
\right.$$
Заавар Бодолт
Заавар.
Бодолт. $z_i=\tg x_i$, $i=1,\dots,n$ ба $\varphi(x)=\dfrac{1}{3}\left(x+\dfrac{1}{x}\right)$ гэвэл
$$z_{s+1}=\dfrac{1}{3}\left(z_s+\dfrac{1}{z_s}\right)=\varphi(z_s),\ s=1,\dots,n\qquad(1)$$
байна.
$(1)$-ээс бүх $z_i$ ижил тэмдэгтэй болох нь гарна. Бид зөвхөн $z_i>0$ тохиолдлыг бодъё. $z_i<0$ байх тохиолдолд бодолт ижил байна.
Бодлогын нөхцөлөөөс
$$z_s=\varphi^n(z_s)$$
болно.
$y=x$ ба $y=\varphi^n({x})$ муруйнууд нь $x>0$ байх огтлолцлын цэг зөвхөн ганцтай\footnote{Энэ өгүүлбэрийг баталгаа ойлгомжгүй байсан тул энд оруулсангүй. Та бүхэн хялбар баталгаа олбол бидэнд ирүүлнэ үү}. Гэтэл $x=\varphi({x})$ бол $x=\varphi^n(x)$ байх ёстой тул энэ эрж буй шийд нь зөвхөн $x=\varphi({x})$-ийн л шийд байна. $$3x=x+\dfrac{1}{x}\Leftrightarrow 2x=\dfrac{1}{x}\Leftrightarrow x=\pm{\dfrac{\sqrt{2}}{2}}.$$ Иймд $(1)$ системийн бодит шийд нь $\left(\dfrac{\sqrt{2}}{2},\dots,{\dfrac{\sqrt{2}}{2}}\right)$ ба $\left(-\dfrac{\sqrt{2}}{2},\dots,-{\dfrac{\sqrt{2}}{2}}\right)$ болно. Өөр бодит шийд байхгүй.
Иймд $\tg{x_i}=\dfrac{\sqrt{2}}{2}$, $i=1,2,\dots,n$ эсвэл $\tg{x_i}=-\dfrac{\sqrt2}{2}$, $i=1,2,\dots,n$ гэсэн шийдтэй.
$y=x$ ба $y=\varphi^n({x})$ муруйнууд нь $x>0$ байх огтлолцлын цэг зөвхөн ганцтай\footnote{Энэ өгүүлбэрийг баталгаа ойлгомжгүй байсан тул энд оруулсангүй. Та бүхэн хялбар баталгаа олбол бидэнд ирүүлнэ үү}. Гэтэл $x=\varphi({x})$ бол $x=\varphi^n(x)$ байх ёстой тул энэ эрж буй шийд нь зөвхөн $x=\varphi({x})$-ийн л шийд байна. $$3x=x+\dfrac{1}{x}\Leftrightarrow 2x=\dfrac{1}{x}\Leftrightarrow x=\pm{\dfrac{\sqrt{2}}{2}}.$$ Иймд $(1)$ системийн бодит шийд нь $\left(\dfrac{\sqrt{2}}{2},\dots,{\dfrac{\sqrt{2}}{2}}\right)$ ба $\left(-\dfrac{\sqrt{2}}{2},\dots,-{\dfrac{\sqrt{2}}{2}}\right)$ болно. Өөр бодит шийд байхгүй.
Иймд $\tg{x_i}=\dfrac{\sqrt{2}}{2}$, $i=1,2,\dots,n$ эсвэл $\tg{x_i}=-\dfrac{\sqrt2}{2}$, $i=1,2,\dots,n$ гэсэн шийдтэй.