ММО-20, 10-р анги
Бодлогын тоо: 6 Хугацаа: 540 мин
1. $a$ талтай зөв гурвалжны талбайг хагаслан хуваагч хамгийн богино шугамын уртыг ол.
Заавар Бодолт
Заавар.
Бодолт. Энэ бодлогын бодолт эргэлзээтэй, дутуу байсан тул энд оруулсангүй. Муруйн урт зэрэг нэлээд төвөгтэй ойлголтуудыг агуулж байгаа тул энгийн түвшинд шийдэгдэх боломжгүй бодлого юм.
2. Зөв олон өнцөгтийн оройнууд дээр 1, 1-ээр оршигч цэгүүд тогтмол хурдтайгаар нэг чиглэлд зэрэг хөдлөв. Тодорхой хугацааны дараа аль нэг оройд бүгд уулзсан бол өөр оройд дахин уулзахгүй гэдгийг батал.
Заавар Бодолт
Заавар.
Бодолт. Цэгүүд $t=0$ моментод хөдөлж эхэлсэн ба анх удаагаа $t=T$ моментод ямар нэг $B$ орой дээр бүгд уулзсан гэж үзье. Цэгүүдийн төлөв нь $T-t$ ба $T+t$ моментуудын хувьд тэгш хэмтэй байх тул $t=2T$ моментод цэгүүд ганц ганцаараа оройнууд дээр байх ба хөдөлгөөний төлөв давтагдана. Одоо эсрэгээс нь цэгүүд $B\neq{C}$ орой дээр мөн уулздаг гэж үзвэл төлөв давтагдах чанар ёсоор энэ уулзалт нь $T-s < T$ байх $t=T-s$ моментод бас болсон байх ёстой. Энэ нь $T$-ийн сонголтод харшлав. Иймд цэгүүд $B$ орой дээр $1$ удаа уулзсан бол энэ $B$ орой дээр төгсгөлгүй олон удаа уулзах боловч харин өөр орой дээр уулзалдахгүй.
3. $M=\{(a_1,a_2,\dots,a_n)\mid a_i=\pm1\}$ олонлог дээр
$$(a_1,\dots,a_n)(b_1,\dots,b_n)=(a_1b_1,\dots,a_nb_n)$$
гэж үйлдэл тодорхойлов. $M$-ийн $k$ элементтэй $B$ дэд олонлогийн хувьд
$|B\cup cB|\le\dfrac{k^2}{2^n}$ байх $c$ гэсэн элемент $M$-ээс олдохыг батал. Үүнд: $|A|$ нь $A$ олонлогийн элементийн тоо юм.
Заавар Бодолт
Заавар.
Бодолт. $|M|=2^n$ байх нь илэрхий. Эсрэгээс нь $M$ олонлогийн ямар ч элементийн хувьд $|B\cap{cB}|>\dfrac{h^2}{2^n}$ байдаг гэж үзье. $M=\{c_1,c_2,\dots,c_{2^n}\}$ ба бидний үзэж байгаагаар $c_1{B},\dots,c_{2^n}B$ олонлогууд дотор $B$-ийн элемент $\dfrac{k^2}{2^n}\cdot{2^n}=k^2$-ээс илүү орно. (Элементүүд давхар тоологдож болох юм). Иймд $B$-ийн ядаж нэг элемент $b$ нь $c_1{B},\dots,c_{2^n}B$ олонлогуудын дотор $k+1$ удаа давтагдан орно. Өөрөөр хэлбэл, $b=c_{j_1}b_{i_1}=\dots=c_{j_{(k+1)}}b_{i_{(k+1)}}$ байна. $|B|=k$ учир Дирихлейн зарчмаар $b_{i_t}=b_{i_s}$ байх ялгаатай $2$ индекс $i_t\neq{i_s}$ заавал олдоно. Тэгвэл $b_{i_t}=b_{i_s}$ ба $c_{j_t}b_{i_t}=c_{j_s}b_{i_s}$ гэдгээс $c_{j_t}=c_{j_s}$ гэж гарах тул энэ нь $c_{j_t}\neq{c_{j_s}}$ байх ёстойд зөрчив. Бодлого бодогдов.
4. $5(xyz+x+z)=222(yz+1)$ тэгшитгэлийн натурал тоон шийдийг ол.
Заавар Бодолт
Заавар.
Бодолт. $\dfrac{222}{5}=44+\dfrac{2}{5}=\dfrac{xyz+x+z}{yz+1}=x+\dfrac{z}{yz+1}$ $x\in{N}$, $0<\dfrac{z}{yz+1}<1$ тул $x=44$, $z=2$, $yz+1=5$, $yz=4$, $y=2$ гэж гарна.
5. Дараах тэгшитгэл бод.
$$\left\{\dfrac{2x+1}{3}\right\}=\left\{\dfrac{3x-1}{2}\right\}$$
Үүнд: $\{a\}$ гэдэг нь $a$ тооны бутархай хэсэг юм.
Заавар Бодолт
Заавар.
Бодолт. $a=[a]+\{a\}$ тул $\dfrac{3x-1}{2}-\dfrac{2x+1}{3}=\left[\dfrac{3x-1}{2}\right]-\left[\dfrac{2x+1}{3}\right]=\dfrac{5(x-1)}{6}$ нь бүхэл тоо байх ёстой. Иймд $\dfrac{5(x-1)}{6}=k$, $x=1+\dfrac{6}{5}k$, $k\in\mathbb Z$
6. Гүдгэр 5 өнцөгтийн хувьд $1<\dfrac{\sum d}{p}<2$ тэнцэтгэл биш биелэхийг батал. Үүнд $\sum d$ нь диагоналиудын нийлбэр, $p$ нь периметр болно. Мөн а) $\dfrac{\sum d}{p}>1.99$; б) $\dfrac{\sum d}{p}<1.01$ байх таван өнцөгтийг тус тус байгуул.
Заавар Бодолт
Заавар.
Бодолт. Хялбар батлагдах дараах тэнцэтгэл бишүүдээс манай тэнцэтгэл биш шууд гарна.
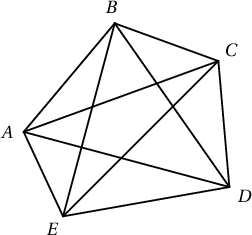 \begin{gather*}
|AB|+|BC|+|CD|+|DA| < 2(|BD|+|CA|)\\
|BC|+|CD|+|DE|+|EB| < 2(|BD|+|CE|)\\
|AC|+|CD|+|DE|+|EA| < 2(|CE|+|AD|)\\
|AB|+|BD|+|DE|+|AE| < 2(|BE|+|AD|)
\end{gather*}
тэнцэтгэл бишүүдийг нэмбэл $3p+\sum{d}<4\sum{d}$ буюу $1<\dfrac{\sum{d}}{p}$ гарна. Харин $|AB|+|BC|>|AC|$, $|CD|+|DE|>|CE|$, $|CD|+|BC|>|BD|$, $|DE|+|EA|>|AD|$, $|EA|+|AB|>|BE|$-үүдээс $\dfrac{\sum{d}}{p}<2$ гарна.
\begin{gather*}
|AB|+|BC|+|CD|+|DA| < 2(|BD|+|CA|)\\
|BC|+|CD|+|DE|+|EB| < 2(|BD|+|CE|)\\
|AC|+|CD|+|DE|+|EA| < 2(|CE|+|AD|)\\
|AB|+|BD|+|DE|+|AE| < 2(|BE|+|AD|)
\end{gather*}
тэнцэтгэл бишүүдийг нэмбэл $3p+\sum{d}<4\sum{d}$ буюу $1<\dfrac{\sum{d}}{p}$ гарна. Харин $|AB|+|BC|>|AC|$, $|CD|+|DE|>|CE|$, $|CD|+|BC|>|BD|$, $|DE|+|EA|>|AD|$, $|EA|+|AB|>|BE|$-үүдээс $\dfrac{\sum{d}}{p}<2$ гарна.
а)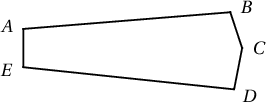 хэлбэрийн таван өнцөгтийн хувьд $\sum d/p>1.99$ байна.
хэлбэрийн таван өнцөгтийн хувьд $\sum d/p>1.99$ байна.
б)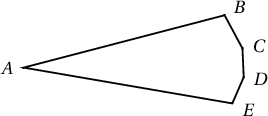 хэлбэрийн таван өнцөгтийн хувьд $\sum d/p <1.01$ байна.
хэлбэрийн таван өнцөгтийн хувьд $\sum d/p <1.01$ байна.

а)

б)
