ММО-21, 10-р анги
Бодлогын тоо: 6 Хугацаа: 540 мин
1. $1985$ ширхэг натурал тооноос тогтох $M$ олонлог өгчээ. $M$ олонлогийн ямар ч тоо нь $a+21$-ээс их анхны тоонд үл хуваагдана. Тэгвэл
- $a\le 9$ бол $M$ олонлогийн ямар нэг $2$ элементийн геометр дундаж нь бүхэл тоо байхыг батал.
- $a\ge 10$ бол аль ч хоёр элементийн нь геометр дундаж бүхэл тоо биш байхаар тийм $M$ олонлог олдохыг үзүүл.
Заавар Бодолт
Заавар.
Бодолт. а) Тохиолдолд өгсөн тоонууд нь $2, 3, 5,\dots, 23, 29$ гэсэн $10$ анхны тоонд хуваагдах ёстой. $M$ олонлогийн ямар ч тоо нь $x=2^{a_1}3^{a_2}\cdots 29^{a_{10}}$, $a_i \geqslant 0$ хэлбэртэй байна. Хэрэв $a_i=b_i\pmod{2}$, $i=1, 2,\dots, 10$ бол $xy$ нь квадрат хэлбэртэй болно. Энд $y=2^{b_1}3^{b_2}\cdots 29^{b_{10}} \in M$ тоо. Нэгэнт $A=\{(a_1, a_2,\dots,a_{10})\mid a_i=0,1\}$, $|A|=2^{10} < 1985$ тул $a_i \equiv b_i\pmod{2}$, $i=1,\dots,{10}$ байх $2$ тоо $x, y \in M$ заавал олдоно.
б) $a \geqslant 10$ үед $M$ олонлогийн элементүүд нь $2, 3, 5,\dots,31$ гэсэн $11$ анхны тоонд хуваагдана. $2^{11}>1985$ тул энэ нөхцөлийг хангасан олонлогийг олж болно. Тухайлбал $2, 3,\dots, 31, 2\cdot3, 2\cdot5,\dots, 29\cdot31,\dots, 2\cdot3\cdots 31$ гэсэн $2^{11}-1$ ширхэг тооны аль ч $1985$-аас нь тогтох олонлог байж болно.
б) $a \geqslant 10$ үед $M$ олонлогийн элементүүд нь $2, 3, 5,\dots,31$ гэсэн $11$ анхны тоонд хуваагдана. $2^{11}>1985$ тул энэ нөхцөлийг хангасан олонлогийг олж болно. Тухайлбал $2, 3,\dots, 31, 2\cdot3, 2\cdot5,\dots, 29\cdot31,\dots, 2\cdot3\cdots 31$ гэсэн $2^{11}-1$ ширхэг тооны аль ч $1985$-аас нь тогтох олонлог байж болно.
2. Дараах тэнцэтгэлийг батал.
$$\sqrt{3}\tg^5 20^\circ-9\tg^4 20^\circ+30\tg^2 20^\circ+9\sqrt3\tg20^\circ=9+6\sqrt3\tg^3 20^\circ$$
Заавар Бодолт
Заавар.
Бодолт. $\tg3\alpha=\dfrac{3\tg\alpha-\tg^3\alpha}{1-3\tg^2\alpha}$ томьёонд $\alpha=20^{\circ}$ авбал
$$\sqrt{3}=\dfrac{3\tg20^{\circ}-\tg^320^{\circ}}{1-3\tg^220^{\circ}}$$
буюу
$$\tg^320^{\circ}-3\sqrt{3}\tg^220^{\circ}-3\tg20^{\circ}+\sqrt{3}=0\qquad(1)$$
болно. $(1)$-ийн хоёр талыг $\sqrt{3}\tg^2 20^{\circ}-3\sqrt{3}$-аар үржүүлж эмхэтгэвэл манай тэнцэл батлагдана.
3. $D_1BD_{n+1}$ гурвалжны $D_1D_{n+1}$ тал дээр $D_2; D_3;\dots;D_n$ цэгүүд дараалан өгөгджээ. $D_1BD_{n+1}$, $D_kBD_{k+1}$ гурвалжнуудад багтсан тойргийн радиусуудыг харгалзан $r$, $r_k$; тэдгээрийн $B$ өнцөгт гадаад багтсан тойргийн радиусыг $R$, $R_k$, ($k=1,2,\dots,n$) гэж тэмдэглэвэл
$$\dfrac{r_1\cdots r_n}{R_1\cdots R_n}=\dfrac{r}{R}$$
байхыг батал.
Заавар Бодолт
Заавар.
Бодолт. $n=2$ үед баталбал хангалттай гэдэг нь илэрхий. $M$ нь $AB$ тал дээр байгаа цэг ба $\angle{ABC}=\beta$, $\angle{BCA}=\gamma$, $\angle{CAB}=\alpha$, $\angle{AMC}=\delta$ гэвэл
$$|AB|=r\ctg{\dfrac{\alpha}{2}}+r\ctg{\dfrac{\beta}{2}}\qquad(1)$$
болно.
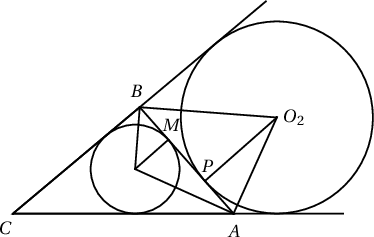$P$ нь гадаад багтсан тойргийн $AB$ талыг шүргэсэн цэг ба $O_2$ нь уг тойргийн төв бол $\angle{APO_2}=\angle{BPO_2}=\dfrac{\pi}{2}$ тул $$|AB|=R\tan\dfrac{\alpha}{2}+R\tan\dfrac{\beta}{2}$$
болно. Иймд $(1)$-ээс
$$\dfrac{r}{R}=\dfrac{\tg\dfrac{\alpha}{2}+\tg\dfrac{\beta}{2}}{\ctg\dfrac{\alpha}{2}+\ctg\dfrac{\beta}{2}}=\tg\dfrac{\alpha}{2}\cdot\tg\dfrac{\beta}{2}\qquad(2)$$
болно. Үүний адилаар $\angle{ACM}$ ба $\angle{MCB}$-д харгалзах тойргуудын хувьд $\dfrac{r_1}{R_1}=\tg\dfrac{\alpha}{2}\cdot\tg\dfrac{\delta}{2}$, $\dfrac{r_2}{R_2}=\tg\dfrac{\pi-\delta}{2}\cdot\tg\dfrac{\beta}{2}=\ctg\dfrac{\delta}{2}\cdot\tg\dfrac{\beta}{2}$ болох тул $\dfrac{r_1r_2}{R_1R_2}=\dfrac{r}{R}$ болох нь илэрхий.
4. $A^2$ нь дараалсан 2 тооны кубуудын ялгавар бол $A$ нь дараалсан 2 тооны квадратуудын нийлбэр гэж батал.
Заавар Бодолт
Заавар.
Бодолт. $(x+1)^3-x^3=3x^2+3x+1=y^2$ тэгшитгэлийг бодоход шилжив. Үүнийг 4-өөр үржүүлэх замаар $3(2x+1)^2=(2y-1)(2y+1)$ хэлбэртэй бичвэл $2y-1, 2y+1$ нь харилцан анхны тоонууд тул дараах 2 тохиолдол л байж болно.
а) $\begin{cases}2y-1=3m^2\\2y+1=n^2\end{cases}$, б) $\begin{cases}2y-1=m^2\\2y+1=3n^2\end{cases}$, $(m, n)=1$
б) тохиолдолд $m=2k+1$ гэж авбал $2y=4k^2+4k+2=2 [(k+1)^2+k^2]$ болно. Харин а) тохиолдол байж үл болно. Учир нь энэ үед $n^2-3m^2=2$ гэж гарах ба энэ нь ямар ч бүхэл тооны квадратыг 3-д хуваахад 0 юм уу 1, үлдэнэ гэдэгт харшилна.
а) $\begin{cases}2y-1=3m^2\\2y+1=n^2\end{cases}$, б) $\begin{cases}2y-1=m^2\\2y+1=3n^2\end{cases}$, $(m, n)=1$
б) тохиолдолд $m=2k+1$ гэж авбал $2y=4k^2+4k+2=2 [(k+1)^2+k^2]$ болно. Харин а) тохиолдол байж үл болно. Учир нь энэ үед $n^2-3m^2=2$ гэж гарах ба энэ нь ямар ч бүхэл тооны квадратыг 3-д хуваахад 0 юм уу 1, үлдэнэ гэдэгт харшилна.
5. $$\sqrt{\cos2x+\sin x-\cos x}+\sqrt[4]{\pi^2-x}+\sqrt{\pi+x}>\pi$$
тэнцэтгэл бишийг бод.
Заавар Бодолт
Заавар.
Бодолт. $x>0$ бол $\sqrt{\pi+x}>\sqrt{\pi}$, $x<0$ бол $\sqrt[4]{\pi^2-x}>\sqrt{\pi}$, $x=0$ бол $2\sqrt{\pi}>\sqrt{\pi}$ байх учир манай тэнцэтгэл бишийн шийд нь тодорхойлогдох муж юм. Иймд $(\cos x-\sin x)(\cos x+\sin x-1)\geqslant0; \pi^2-x\geqslant0; x+\pi\geqslant0$ системийг бодож шийдийг олно.
6. Хоёр гурвалжны талууд $a_1,a_2,a_3$; $b_1,b_2,b_3$ бөгөөд дурын сондгой $n$-ийн хувьд
$$a_1^n+a_2^n+a_3^n=b_1^n+b_2^n+b_3^n$$
бол энэ хоёр гурвалжин тэнцүү гэж батал.
Заавар Бодолт
Заавар.
Бодолт. $a_1\leqslant a_2\leqslant a_3, b_1\leqslant b_2\leqslant b_3$ гэж үзэж болно. Хэрэв $a_3>b_3$ бол $a_3=b_3+\varepsilon$ $\varepsilon>0$; $a_3^n=(b_3+\varepsilon)^n\geqslant b_3^n+n\cdot\varepsilon\cdot b_3^n-1$ болно. Тэгвэл
$$b_3^n+n\varepsilon b_3^{n-1}>b_3^n+b_2^n+b_1^n$$
$$n\varepsilon b_3^{n-1}>b_2^n+b_1^n,\quad n>\frac{b_2^n+b_1^n}{b_3^{n-1}\varepsilon}$$
байхаар $n$-ийг сонгож авсан үед $a_3^n>b_1^n+b_2^n+b_3^n$ тул бодлогын нөхцөлд харшлав. Иймд $a_3=b_3$ болно. Үүний дараа энэ сэтгэлгээгээр $a_2=b_2, a_1=b_1$ гэж тус тус гарна.
Асуулт. Дурын бодит тоо $a_1\leqslant ...\leqslant a_{k_1}, b_1\leqslant\ldots\leqslant b_{k_2}$ ба дурын сондгой натурал тоо $n$-ийн хувьд $a_1^n+\ldots+a_{k_1}^n=b_1^n+\ldots+b_{k_2}^n$ бол $k_1=k_2, a_1=b_1,\ldots, a_{k_1}=b_{k_1}$ болохыг батал.
Асуулт. Дурын бодит тоо $a_1\leqslant ...\leqslant a_{k_1}, b_1\leqslant\ldots\leqslant b_{k_2}$ ба дурын сондгой натурал тоо $n$-ийн хувьд $a_1^n+\ldots+a_{k_1}^n=b_1^n+\ldots+b_{k_2}^n$ бол $k_1=k_2, a_1=b_1,\ldots, a_{k_1}=b_{k_1}$ болохыг батал.