Заавар.

Бодолт. Тодорхойлогдох муж нь $D\colon x-1>0, x-1\neq 1$ тул $x>1$, $x\neq 2$ байна. $$\log_{x-1}(x+1)>\log_{x^2-1}(x+1)\Leftrightarrow\dfrac{1}{\log_{x+1}(x-1)}>\dfrac{1}{\log_{x+1}(x^2-1)}$$ $t=\log_{x+1}(x-1)$ гэвэл $$\Leftrightarrow\dfrac{1}{t}>\dfrac{1}{t+1}\Leftrightarrow \dfrac{1}{t(t+1)}>0\Leftrightarrow t<-1\cup t>0$$ байна. $x+1>1$ тул $$\log_{x+1}(x-1)<-1\Leftrightarrow x-1 < \dfrac{1}{x+1}\Leftrightarrow x<\sqrt{2}$$ эсвэл $$\log_{x+1}(x-1) >0 \Leftrightarrow x-1 > 1\Leftrightarrow x>2$$ байна. Тодорхойлогдох мужаа тооцвол $1 < x <\sqrt2$ эсвэл $x>2$ байна.

Заавар.

Бодолт. $0 < a\le b\le c<1$ гэж үзэж болно. Тэгвэл $a+b+c=2$ гэдгээс $a\le\dfrac23$, $b\ge\dfrac12$, $c\ge\dfrac23$ гэж гарна. Иймд $$a^{2^n}+b^{2^n}+c^{2^n}>\dfrac{1}{2^{2^n}}+\dfrac{2^{2^n}}{3^{2^n}}$$ болно. Одоо $$\dfrac{1}{2^{2^n}}+\dfrac{2^{2^n}}{3^{2^n}}>\dfrac{1}{2^{2^n}-2}$$ болохыг баталъя. $$\dfrac{1}{2^{2^n}}+\dfrac{2^{2^n}}{3^{2^n}}=\dfrac{3^{2^n}+2^{2\cdot 2^n}}{6^{2^n}}>\dfrac{1}{2^{2^n}-2}$$ $$\Leftrightarrow 6^{2^n}+2^{3\cdot 2^n}-2\cdot 3^{2^n}-2^{(2^{n+1}+1)}>6^{2^n}$$ $$\Leftrightarrow 8^{2^n}-2\cdot (3^{2^n}+4^{2^n})>0$$ болно. Нөгөө талаас $k\ge 2$ үед $8^k-2\cdot (3^k+4^k)>0$ болохыг хялбархан баталж болно. Үнэндээ $$8^k-2\cdot (3^k+4^k)>0\Leftrightarrow 1-2\cdot\bigg\{\left(\dfrac{3}{8}\right)^k+\left(\dfrac{4}{8}\right)^k\bigg\} >0$$ ба сүүлийн тэнцэтгэл биш нь $$1-2\cdot\bigg\{\left(\dfrac{3}{8}\right)^k+\left(\dfrac{4}{8}\right)^k\bigg\} > 1-2\cdot\bigg\{\left(\dfrac{3}{8}\right)^2+\left(\dfrac{4}{8}\right)^2\bigg\}=\dfrac{7}{32} >0$$ тул үнэн юм.

Заавар.

Бодолт. Өгсөн хоёр тойрог дотоод байдлаар шүргэлцсэн тохиолдлыг авч үзье. $P$ дээр төвтэй $\dfrac{PA_1}{PA}=k$ коэффициенттэй гомотетийг $\varphi$ гэе. $\ell$ нь $P$ цэг дээрх шүргэгч байг. 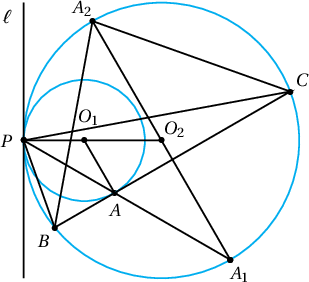$O_1P\perp\ell\perp O_2P$ тул $O_1$ цэг нь $PO_2$ хэрчим дээр оршино. Иймд адил хажуут гурвалжин $PO_1A$, $PO_2A$ нь төстэй ба $\varphi(A)=A_1$ тул $\varphi(O_1)=O_2$ болно. Нэгэнт $\varphi(A)=A_1$ тул $\varphi([O_1A])=[O_2A_1]$ ба $O_1A\parallel O_2A_1$ болно. $O_1A\perp BC$ гэдгээс $O_2A_1\perp BC$ гэж гарах тул $O_2A_1$ нь $[BC]$-г таллан хуваана. Иймд $\triangle A_2BC$ нь адил хажуут тул $$\angle BPA_1=\angle BA_2A_1=\angle A_1A_2C=\angle A_1PC$$ болно. Өгсөн хоёр тойрог гадаад байдлаар шүргэлцсэн тохиолдолд мөн үүнтэй адил болно.

Заавар.

Бодолт. $x=y=0$ гэвэл $$f(0)=[f(0)]^2-f(0)+1\Rightarrow f(0)=1$$ болно. $y=1$ гэвэл \begin{align*} f(x)&=f(x)\cdot f(1)-f(x+1)+1\\ &=2f(x)-f(x+1)+1 \end{align*} тул $$f(x+1)=f(x)+1\qquad(1)$$ гэж гарна. $(1)$-ээс аливаа $m\in\mathbb N$-ийн хувьд $$f(x+m)=f(x)+m$$ ба $f(1)=2$ гэдгээс $\forall m\in\mathbb Z$ хувьд $f(m)=m+1$ болохыг харуулах төвөгтэй биш. Иймд \begin{align*} 2&=f(1)=f\left(n\cdot\dfrac{1}{n}\right)\\ &=f(n)\cdot f\left(\dfrac{1}{n}\right)-f\left(n+\dfrac{1}{n}\right)+1\\ &=(n+1)\cdot f\left(\dfrac{1}{n}\right)-n-f\left(\dfrac{1}{n}\right)+1\\ &=n\cdot f\left(\dfrac{1}{n}\right)-n+1 \end{align*} учраас $f\left(\dfrac{1}{n}\right)=\dfrac{1}{n}+1$ болно. Түүнчлэн аливаа $x=\dfrac{m}{n}$, $m\in\mathbb Z$, $n\in\mathbb N$ тооны хувьд \begin{align*} f\left(\dfrac{m}{n}\right)&=f\left(m\cdot\dfrac{1}{n}\right)\\ &=f(m)\cdot f\left(\dfrac{1}{n}\right)-f\left(m+\dfrac{1}{n}\right)+1\\ &=(m+1)\cdot \left(\dfrac{1}{n}+1\right)-\left(m+\dfrac{1}{n}+1\right)+1\\ &=\dfrac{m}{n}+1 \end{align*} учир $f(x)=x+1$ болов.

Заавар.

Бодолт. Өгсөн нөхцөлийг $a_{k+1}=\dfrac{a_k(a_k+n)}{n}$, $\dfrac{1}{a_{k+1}}=\dfrac{1}{a_k}-\dfrac{1}{a_k+n}$ гэж бичиж болно. Үүнийг $0\le k\le n-1$ байх $k$-аар нийлбэрчилбэл $$\dfrac{1}{a_n}=\dfrac{1}{a_0}-\sum_{i=0}^{n-1}\dfrac{1}{n+a_i}$$ болно. $a_0=\dfrac12$ ба $a_i>0$ тул $$\dfrac{1}{a_n}=\dfrac{1}{a_0}-\sum_{i=0}^{n-1}\dfrac{1}{n+a_i}\ge 2-n\cdot\dfrac{1}{n}=1$$ буюу $a_n < 1$ болно. Нэгэнт $a_k < a_{k+1}$ тул дурын $k < n$-ийн хувьд $a_k < a_n <1$ болох нь батлагдлаа. Эндээс $$\dfrac{1}{n+1} < \dfrac{1}{a_k+n}<\dfrac{1}{n}$$ болно. Иймд $$\dfrac{1}{a_n}=\dfrac{1}{a_0}-\sum_{i=0}^{n-1}\dfrac{1}{n+a_i} < 2-\dfrac{n}{n+1}=\dfrac{n+2}{n+1}$$ буюу $$a_n>\dfrac{n+1}{n+2}=1-\dfrac{1}{n+2}>1-\dfrac{1}{n}$$ болж бодлого бодогдов.

Заавар.

Бодолт. Анх байсан нийт номын тоог $m$ гэе. $m$ сондгой, $n$ тэгш байхаас бусад тохиолдолд бүх хайрцаг тэнцүү номтой болох боломжтой гэдгийг харуулъя. Энэ нь аль нэг хоёр тавиурт ном нэмэх замаар бүгдийг нь тэнцүүлэх бодлоготой эквивалент гэдгийг харахад төвөгтэй биш юм. Иймд хоёр тавиурт ном нэмэх бодлогыг бодъё.

$m$ сондгой, $n$ тэгш үед нийт номын тоо үргэлж сондгой байна. Нөгөө талаас бүх хайрцаг тэнцүү тооны номтой болсон гэвэл энэ тоо тэгш байх ёстой. Иймд энэ тохиолдолд номын тоог тэнцүүлэх боломжгүй.

$n=2k+1$ байг. Хэсэг үйлдлийн дараа аль нэг хайрцагт бусдаасаа яг нэгээр илүү тооны ном нэмэгдсэн байхаар үйлдэл хийж чадвал бүгдийг нь тэнцүүлж болох нь ойлгомжтой. $n=2k+1$ үед энэ нь боломжтой юм. $$\{1,2\}, \{1,3\}, \{4,5\},\ldots, \{2k, 2k+1\}$$ үйлдлээр 1-р хайрцагт бусдаас нь яг 1-ээр илүү тооны ном нэмэгдэнэ. Энд $\{a,b\}$ нь $a$, $b$-р тавиурт ном нэмэх үйлдлийг тэмдэглэж байгаа болно.

$m$, $n$ тэгш үед хамгийн цөөн тооны номтой хоёр тавиур дээр ном нэмэх үйлдлийг давтан хийсээр бүх тавиурт тэнцүү тооны ном тавьж болно гэдгийг харуулъя. Тавиуруудад бүгд тэнцүү биш $$a_1\le a_2\le \cdots\le a_n$$ ширхэг ном тавигдсан гэе. Дээрх дурдсан үйлдлээр хамгийн олон ба хамгийн цөөн хоёрын зөрөө багасаагүй гэе. Энэ нь дараах хоёр боломжтой. а) $a_1=a_2=a_3$ б) $a_2=a_3=\dots=a_n$

а) тохиолдолд хамгийн цөөн номтой тавиурын тоо 2-оор цөөрнө. Иймд үйлдлээ давтан хийсээр $a_1$ номтой тавиурын тоог $1$ эсвэл $2$ болгож болно. Хэрвээ $1$ бол дахин нэг удаа үйлдэл хийхэд а) тохиолдол гарах боломжгүй тул эсвэл б) тохиолдол эсвэл бидний сонирхож байгаа зөрөө багасна. Харин $2$ бол дараагийн үйлдлээр хамгийн олон ба хамгийн цөөн хоёрын зөрөө багасна.

б) тохиолдолд $a_1'=a_1+1 < a_3=a_4=\dots=a_{n} < a_2'=a_2+1$ байна. Учир нь $a_1'=a_3$ бол $m$ сондгой болоход хүрнэ. Иймд дараагийн үйлдлээр хамгийн олон ба хамгийн цөөн хоёрын зөрөө багасана.

Нөгөө талаас хамгийн олон ба хамгийн цөөн хоёрын зөрөөг төгсгөлгүй олон удаа багасах боломжгүй. Иймд хэсэг алхамын дараа тавиур бүр тэнцүү тооны номтой болно.