Заавар.

Бодолт. Бодолт хоёр шатаар хийгдэнэ.

а) Дурын $n\in\mathbb N$-ийн хувьд $\sqrt{4n+3}$ нь рационал тоо биш гэж үзүүлье. Хэрэв $$\sqrt{4n+3}=\dfrac{p}{q},\quad (p,q)=1$$ бол $4n+3=\dfrac{p^2}{q^2}$ байна. Эндээс $$3q^2\equiv p^2\pmod{4}\Rightarrow p\equiv q\equiv 0\pmod{2}$$ болж $(p,q)=1$ гэдэгт зөрчинө. Иймд $\sqrt{4n+3}$ нь иррационал тоо байна.

б) $k\in\mathbb N$ нь бүтэн квадрат биш байхад $a_0$, $a_1$, $a_2$, $a_3$ бүхэл тоонуудын хувьд $$a_0+a_1\sqrt[4]{k}+a_2\sqrt[4]{k^2}+a_3\sqrt[4]{k^3}=0$$ бол $a_0=a_1=a_2=a_3=0$ байхыг үзүүлье.

Эсрэгээс нь ийм биш гэж үзье. Өөрөөр хэлбэл $$(a_0,a_1,a_2,a_3)\neq(0,0,0,0)$$ боловч дээрх харьцаа биелэх $(a_0,a_1,a_2,a_3)$ дөрвөл оршин байна гэж үзье. Ийм дөрвөлүүдээс зохиож болох $$f(x)=a_0+a_1x+a_2x^2+a_3x^3$$ олон гишүүнтүүдээс хамгийн бага зэрэгтэй нь $f(x)$ гэе. $g(x)=x^4-k$ гээд $g(x)$-г $f(x)$-д хуваая. $$g(x)=f(x)\cdot q(x)+r(x),\quad \deg r(x)<\deg f(x)$$ гэе. $$r(x)=b_0+b_1x+b_2x^2+b_3x^3$$ гэвэл $g(\sqrt[4]{k})=f(\sqrt[4]{k})=0$ тул $r(\sqrt[4]{k})=0$ болно. Иймд $f(x)$-ийн тодорхойлолтоос $$(b_0,b_1,b_2,b_3)=(0,0,0,0)$$ болно. Иймд $g(x)=f(x)\cdot q(x)$ болов. Нөгөө талаас $g(x)$ нь тэг биш хоёр олон гишүүнтийн үржвэрт $$g(x)=(x-\sqrt[4]{k})(x^3+\sqrt[4]{k}x^2+\sqrt[4]{k^2}x+\sqrt[4]{k^3})$$ $$g(x)=(x+\sqrt[4]{k})(x^3-\sqrt[4]{k}x^2+\sqrt[4]{k^2}x-\sqrt[4]{k^3})$$ $$g(x)=(x^2-\sqrt[4]{k^2})(x^2+\sqrt[4]{k^2})$$ гэж задарна. Гэтэл а)-д баталснаар $\sqrt[4]{k^2}=\sqrt{k}$ нь рационал тоо биш учир үржигдэхүүн бүрд ядаж нэг рационал биш коэффициент орж байна. Иймд $g(x)=f(x)\cdot q(x)$ гэсэн задрал байж болохгүй юм. Энэ зөрчил нь $$a_0+a_1\sqrt[4]{k}+a_2\sqrt[4]{k^2}+a_3\sqrt[4]{k^3}=0$$ байх ядаж нэг тэг биш дөрвөл олдоно гэж авснаас болжээ.

Заавар.

Бодолт. Өгөгдсөн тоонууд нь $$a_1\le a_2\le\dots\le a_{mk}$$ гэе. Аль ч $k$ нь арифметик прогресс үүсгэх ба $k+1 < mk$ тул $$a_1,a_2,\ldots,a_{k-1},a_k$$ ба $$a_1,a_2,\ldots,a_{k-1},a_{k+1}$$ нь үл буурах арифметик прогрессууд юм. Иймд $a_k=a_{k+1}$ болно. Эндээс $k>3$ тул $a_{k}$, $a_{k+1}$ тоонуудыг агуулсан аливаа $k$ ширхэг тоо бүгд $a_k$-тай тэнцүү болов. Иймд өгөгдсөн бүх тоонууд тэнцүү.

Заавар.

Бодолт. Лемм. $G=(V,E)$ графын хувьд $|V|=5$ граф ба $K_3\not\subseteq G$, $K_3\not\subseteq\overline{G}$ бол $G=C_5$ байна.

Хэрвээ 5 оройтой графын орой бүрийн зэрэг 2 бол $C_5$ байх нь ойлгомжтой. Ямар нэг $x$ оройн зэрэг $2$-оос их байг. Тэгвэл гурвалжин агуулахгүй тул $x$ оройтой хөрш оройнууд ирмэгээр холбогдохгүй байх ёстой. Энэ тохиолдолд $\overline{G}$ нь гурвалжин агуулна. Ямар нэг $x$ оройн зэрэг $2$-оос бага байг. Тэгвэл $\overline{G}$ графын хувьд $x$ оройн зэрэг $2$-оос их байна. Леммийн нөхцөлд $G$ ба $\overline{G}$ нь тэгш эрхтэй тул лемм батлагдав.

Өгсөн 6 цэг ба тэдгээрийг холбосон 1-р өнгийн хэрчмүүдээр үүсэх графыг авч үзье. Энэ графын аль ч 5 оройтой дэд хэсэг нь $C_5$ биш байг. Тэгвэл аль ч 5 оройг авахад ижил өнгийн гурвалжин олдох тул дор хаяж 2 ширхэг ижил өнгийн гурвалжин олдох нь ойлгомжтой.

Иймд аль нэг 5 оройгоор үүсэх хэсэг нь $C_5$ байсан гэе. Үлдэх оройг $x$ гэе. Зурагт үзүүлсэнтэй адилаар ирмэгийг хэрчмээр, ирмэг бишийг тасархай шугамаар холбосон байг.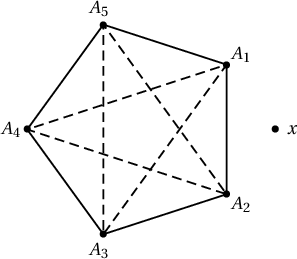 Хэрвээ $x$ оройгоос $0$ эсвэл $1$ хар ирмэг гарсан бол 2 ширхэг тасархай гурвалжин, $4$ эсвэл $5$ хар ирмэг гарсан бол 2 ширхэг хар гурвалжин олдох нь илт. Иймд $x$ оройгоос $2$ эсвэл $3$ хар ирмэг гарсан гэе. Эхлээд $2$ ирмэг гарсан тохиолдлыг авч үзье. Дараалсан хоёр оройтой хараар холбогдсон байг. Тэдгээр нь $A_1$, $A_2$ гэхэд явцуурахгүй. Тэгвэл $xA_1A_2$ хар, $xA_3A_5$ тасархай гурвалжин болно. Дараалсан биш хоёр оройтой хараар холбогдсон байг. Тэдгээр нь $A_1$, $A_3$ гэхэд явцуурахгүй. Энэ тохиолдолд $xA_2A_4$, $xA_2A_5$ гэсэн 2 тасархай гурвалжин олдоно. Одоо $x$ оройгоос $3$ оройтой хар ирмэгээр холбогдсон гэе. Тэдгээр нь дараалсан бол $A_1$, $A_2$, $A_3$ гэхэд явцуурахгүй. Энэ тохиолдолд $xA_1A_2$, $xA_2A_3$ гэсэн хар гурвалжнууд үүснэ. Тэдгээр нь дараалаагүй бол $A_1$, $A_2$, $A_4$ гэхэд явцуурахгүй. Энэ тохиолдолд $xA_1A_2$ хар, $xA_3A_5$ тасархай гурвалжин болно. Иймд аль ч тохиолдолд дор хаяж 2 ширхэг ижил өнгийн гурвалжин олдох нь батлагдлаа.

Заавар.

Бодолт. Дараах тэмдэглэлийг хийе.

$$f^{m+n}(x)=f^{m}(f^{n}(x)),\quad n,m\in\mathbb{N}$$

$f(x)=\dfrac{ax+b}{cx+d}\in{M}$ элементийг авъя. Тэгэхэд $$ad-bc=e\qquad(1)$$ гэе.

$f^2(x)=\dfrac{(a^2+bc)x+b(a+d)}{c(a+d)x+(d^2-bc)}=\dfrac{a_1{x}+b_1}{c_1{x}+d_1}$ болохыг шууд тогтоож болох бөгөөд $f^2(x)$-ийн хувьд $(1)$ илэрхийлэл нь $$(a^2+bc)(d^2-bc)-bc(a+d)^2=e^2\qquad(2)$$ хэлбэртэй болохыг хялбархан харж болно. Яг үүний адилаар $$f^{4}(x)=f^2(f^2(x))=\dfrac{a_2x+b_2}{c_2x+d_2}$$ гарсан гэвэл энэ бутархайн хувьд $(2)$ ёсоор $(1)$-ийг бодоход $a_2d_2-c_2b_2=e^4$ гарна. Ийнхүү $\dfrac{a_nx+b_n}{c_nx+d_n}=f^{2n}(x)$-ийн хувьд $(1)$-ийг бодвол $f^{2n}(x)=f^{2n-1}(f^{2n-1}(x))$ тул индукцээр $$a_nd_n-b_nc_n=(a_{n-1}d_{n-1}-b_{n-1}c_{n-1})^2=(e^{{2}^{n-1}})^2=e^{2^n}$$ болно.

Хэрэв $e\neq{0}$, $\pm1$ бол $M$ олонлог б) чанар ёсоор төгсгөлгүй олон элементтэй болоход хүрнэ. Иймд дурын $f(x)\in{M}$ элементийн хувьд $ad-bc=0$, $\pm1$ байна. Эхлээд $ad-bc=0$ байх тохиолдлыг авч үзье. Хэрэв $a$, $d$, $b$, $c$ тоонуудын аль нэг нь тэгтэй тэнцүү бол тэр үед $M$ олонлог тогтмол тоо агуулахыг хялбархан харж болно. Энэ нь $M$ олонлог тогтмол тоо үл агуулна гэсэнд харшилна. Хэрэв $a\neq{0}$, $b\neq{0}$, $c\neq{0}$, $d\neq{0}$ байсан ч $ad-bc=0$ бол $f(x)=\dfrac{ax+b}{cx+d}=\dfrac{adx+bd}{d(cx+d)}=\dfrac{bcx+bd}{d(cx+d)}=\dfrac{b}{d}$ болж $M$ олонлог тогтмол тоо агуулахад хүрч зөрчил үүсэв. Иймд $ad-bc=0$ байж үл болно.

Одоо $ad-bc=\pm{1}$ байх тохиолдлыг авч үзье. Эндээс $$(a,b)=(a,c)=1, (d,b)=(d,c)=1\qquad(3)$$ байхыг хялбархан харж болно. Хэрэв $f(x)=\dfrac{ax+b}{cx+d}\in{M}$ бол $a)$ ёсоор $g(x)=\dfrac{cx+d}{ax+b}\in{M}$ болно. Одоо в) чанар ёсоор $f(g(x))=g(f(x))$ болно гэдгээс $a(b+c)=c(a+d)$ буюу $ab=cd$ болно. Гэтэл $ad-bc=\pm{1}$, $ab=cd$-аас бид $(3)$-ийг ашиглан $a\mid d$, $d\mid a$ гэж гарна. Иймд $a=\varepsilon{d}$ үүний адилаар $b=\varepsilon{c}$, $\varepsilon=\pm{1}$ болно. Ийнхүү $|a|=|d|$, $|b|=|c|$ болох тул бидний авч үзэж буй тохиолдолд $a$, $b$, $c$, $d\in\mathbb{Z}$ гэдгийг анхаарвал $$a^2-c^2=\pm{1}\qquad(4)$$ болно. Нэгэнт $a-c$, $a+c\in\mathbb{Z}$ учраас $a=0$, $|c|=1$ эсвэл, $|a|=1$, $c=0$ болно. Хэрэв $a=0$, $|c|=1$ бол $f(x)=\dfrac{1}{x}$ эсвэл $f(x)=-\dfrac{1}{x}$ гэж гарна. Хэрэв $|a|=1$, $c=0$ бол $f(x)=x$ буюу $f(x)=-x$ гэж гарна. Ийнхүү $M$ олонлогийн бүх элементүүд зөвхөн дээрх дөрвөн элементийн аль нэгтэй тэнцэх юм. Иймд $M_1=\left\{x,\dfrac{1}{x}\right\}$, $M_2=\left\{x, -x, \dfrac{1}{x}, -\dfrac{1}{x} \right\}$ олонлогууд бодлогын бүх нөхцөлийг хангаж чадна.

Заавар.

Бодолт. Хүмүүсээ $A_1,\dots, A_n$ цэгүүдээр тэмдэглэж, гар барилцсаныг нь хэрчмүүдээр холбоё. Тэгвэл гурвалжин үүсэхгүй байхаар татаж болох хамгийн олон хэрчим нь $\left[\dfrac{n^2}{4}\right]$ байна гэдгийг тодруулбал бодлого бодогдоно. Хамгийн олон хэрчим гарсан цэг нь $A_1$ ба үүнээс $d$ хэрчим гарсан бөгөөд эдгээрийн үзүүрийн цэгүүд нь $A_n, A_{n-1},\dots, A_{n-d+1}$ байг. Тэгвэл $A_n, A_{n-1},\dots, A_{n-d+1}$ цэгүүд нь хоорондоо хэрчмээр холбогдохгүй.

Нийт хэрчмийн тоог $x$, $A$ цэгээс гарсан хэрчмийн тоог $d(A)$ гэвэл $$x\le{d(A_1)+d(A_2)+\dots+d(A_{n-d})}\le{(n-d)d}\le{\left(\dfrac{n-d+d}{2}\right)^2}={\dfrac{n^2}{4}}$$ буюу $x\le{\left[\dfrac{n^2}{4}\right]}$ болно.

Заавар.

Бодолт. Нэгж квадратаа $\dfrac{1}{16}$ талтай 256 жижиг квадратад хуваая. Тэгвэл эдгээр жижиг квадратын аль нэгд нь манай тэмдэглэсэн цэгээс дор хаяад 8 цэг оршино. Энэхүү жижиг квадратаа зурагт үзүүлсэнээр 2 тэнцүү тэгш өнцөгт болгож хуваая. Сонирхож буй 8 цэгээс $k$ ширхэг нь I тэгш өнцөгтөд $8-k$ ширхэг нь II тэгш өнцөгтөд агуулагддаг гэе.



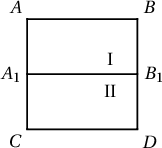
Одоо I тэгш өнцөгтөд буй цэгүүдийг дураараа $A_1,A_2,\ldots,A_k$ гэж дугаарлаад эдгээрийг хэрчмүүдээр холбож $A_1A_2\ldots A_k$ тахир шугам үүсгэвэл $A_iA_j$, $1\le i$, $j\le k $ хэрчмийн урт $|A_1B|=\dfrac{\sqrt{5}}{32}$ диагоналиас үл хэтэрнэ. Иймд $A_1A_2\ldots A_k$ тахир шугамын урт $\dfrac{(k-1)\sqrt{5}}{32}$-ээс үл хэтэрнэ.

Цааш нь II тэгш өнцөгтийн цэгүүдийг дураараа $A_{k+1},\ldots , A_8$ гэж дугаарлавал $A_{k+1}\ldots A_8$ тахир шугамын урт $\dfrac{(7-k)\sqrt{5}}{32}$-гаас үл хэтэрнэ. $|A_kA_{k+1}|\le \dfrac{\sqrt{2}}{16}$ байх нь илэрхий учраас $$|A_1\ldots A_8|\le \dfrac{(k-1)\sqrt{5}}{32} + \dfrac{(7-k)\sqrt{5}}{16}+ \dfrac{\sqrt{2}}{16}=\dfrac{3\sqrt{5}+\sqrt{2}}{16}\le \dfrac{9}{16}$$ болох нь батлагдав.

Заавар.

Бодолт. Параллель 3 шулуунаа харгалзан $m, n, \ell$ гэе. Бодлого 3 тохиолдолтой. Учир нь адил хажуут гурвалжны $\alpha$ өнцөгтэй орой нь $m, n, \ell$ шулуунуудын аль нь дээр ч оршиж болно.

$\alpha$ өнцөгтэй орой нь аль нэг захын шулуун тухайлбал $\ell$ шулуун дээр байх тохиолдлыг эхлээд бодъё.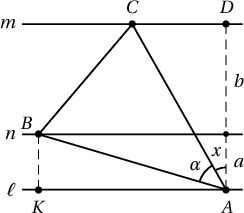 Олох ёстой талбай $S$ нь $$S=\dfrac{1}{2}|AB||AC|\sin{\alpha}=\dfrac{1}{2} |AC|^2 \sin{\alpha}\qquad(1)$$ болно. Одоо $|AC|$-г олъё. $$|AC|=\dfrac{a+b}{\cos{x}},$$ $\angle BKA=90^\circ $ тул $|AB|=\dfrac{b}{\sin(90^\circ-\alpha- x)}$, $|AC|=|AB|$ ба $\sin(90^\circ-\alpha- x)=\cos(\alpha+x)$ гэдгээс $$\dfrac{a+b}{\cos{x}}=\dfrac{b}{\cos(\alpha+x)}\qquad(2)$$ болно. $(2)$-ийг хувиргавал $$[(a+b)\cos{\alpha}-b]\cos{x}=(a+b)\sin{\alpha}\cdot \sqrt{1-\cos^2{x}}\qquad(3)$$ хэлбэртэй болно. $(3)$-ийн 2 талыг квадрат зэрэгт дэвшүүлж, төсөөтэй гишүүдийг эмхэтгэвэл

$$\cos^2{x}=\dfrac{(a+b)^2\sin^2{\alpha}}{a^2+2b(a+b)(1-\cos{\alpha})}\qquad(4)$$

болно. $(4)$-ыг $|AC|^2=\dfrac{{(a+b)}^2}{\cos^2{x}}$-д орлуулбал $$|AC|^2=\dfrac{a^2+2b(a+b)(1-\cos{\alpha})}{\sin^2{\alpha}}=\dfrac{a^2+4b(a+b) \sin^2{\frac{\alpha}{2}}}{\sin^2{\alpha}}$$ болох тул $$S=\dfrac{a^2+4b(a+b)\sin^2{\frac{\alpha}{2}}}{2\sin{\alpha}}\qquad(5)$$ боллоо.

Хэрэв гурвалжны $\alpha$ өнцөгтэй орой нь нөгөө захын шулуун $n$ дээр оршвол $(5)$ томьёонд $a, b$-ийн үүрэг солигдож $$S=\dfrac{b^2+4a(a+b)\sin^2{\frac{\alpha}{2}}}{2\sin{\alpha}}$$ болно.

Одоо гурвалжны $\alpha$ өнцөгтэй орой нь дундах шулуун $n$ дээр оршиж байх тохиолдолдлыг авч үзье.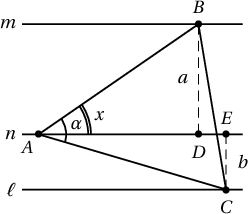 Энэ үед мөн $\alpha=\angle BAC$, $|AB|=|AC|$ болох ба талбай $S$ нь мөн $(1)$ томьёо ёсоор бодогдоно. $|AB|=|AC|=\dfrac{a}{\sin{x}}$, $|AC|=\dfrac{b}{\sin{(\alpha-x)}}$ $$\dfrac{a}{\sin{x}}=\dfrac{b}{\sin{(\alpha-x)}}\qquad(6)$$ $$\sin^2{x}=\dfrac{a^2\sin^2{\alpha}}{a^2+b^2+2ab\cos{\alpha}}\qquad(7)$$ болохыг тус тус олж болно. $$|AC|^2=|AB|^2=\dfrac{a^2}{\sin^2{x}}$$ учраас $(7)$-г ашиглавал $$|AC|^2=\dfrac{a^2+b^2+2ab\cos{\alpha}}{\sin^2{\alpha}}\qquad(8)$$ болно. $(1)$-д $(8)$-ыг орлуулбал $$S=\dfrac{a^2+b^2+2ab\cos{\alpha}}{2\sin{\alpha}}$$ болж бодлого бодогдов.

Заавар.

Бодолт. Дурын бодит тоо $x$-ийн хувьд $$x=[x]+\{x\}\qquad(1)$$ (Энд $[x]$ ба $\{x\}$ нь $x$ тооны бүхэл ба бутархай хэсэг) $0 \le \{x\} < 1$ гэж бичиж болох учраас өгөгдсөн тэгшитгэлийг $$\dfrac{2x-1}{3}-\left\{\dfrac{2x-1}{3}\right\}=\dfrac{x+1}{2}-\left\{\dfrac{x+1}{2}\right\}$$ буюу $$\dfrac{2x-1}{3}+\alpha=\dfrac{x+1}{2}+\beta,\quad 0\le\alpha,\beta\le 1$$ гэж бичиж болно. Эндээс $$\dfrac{2x-1}{3}-\dfrac{x+1}{2}=\beta-\alpha$$ болох ба $0\le\alpha,\beta<1$ гэдгийг анхаарвал $$-1<\dfrac{x-5}{6}<1\Leftrightarrow -1 < x <11$$ болно. Эндээс $0<\dfrac{x+1}{2}<6$ тул $$\left[\dfrac{2x-1}{3}\right]=\left[\dfrac{x+1}{2}\right]=0\lor 1\lor 2\lor 3\lor 4\lor 5$$ тохиолдлуудад шийдийг олж нэгтгэнэ. Жишээ нь $$\left[\dfrac{2x-1}{3}\right]=\left[\dfrac{x+1}{2}\right]=2$$ тохиолдолд $$\left\{\begin{array}{c} 2\le\dfrac{2x-1}{3}<3\\ 2\le\dfrac{x+1}{2}<3 \end{array}\right.\Leftrightarrow \left\{\begin{array}{c} 3.5\le x<5\\ 3\le x<5 \end{array}\right. $$ тул $[3.5,5)$ завсар шийд болно.