Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Вектор, Координатын арга
Бөмбөлгийн тэгшитгэл
$A(-1;7;5\sqrt{2})$ цэгийг дайрсан шулуун $x^2+y^2+z^2=64$ бөмбөрцөгийг $B$ цэгт шүргэх бол $AB$ хэрчмийн уртыг ол.
A. $5$
B. $6$
C. $7$
D. $8$
E. $9$
Векторыг сууриар задлах
$OACB$ квадратын $AC$ талын дундаж цэг $M$ ба $AB$ диагональ $OM$ хэрчимтэй $P$ цэгт огтлолцдог. Хэрэв $\overrightarrow{OA}=\overrightarrow{a\vphantom{OA}}$, $\overrightarrow{OB}=\overrightarrow{b\vphantom{OA}}$ бол $\overrightarrow{PM}$-ийг $\overrightarrow{a\vphantom{OA}}$, $\overrightarrow{b\vphantom{OA}}$-ээр илэрхийл.
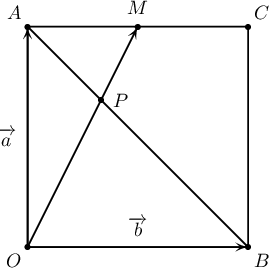

A. $\dfrac{2\overrightarrow{a\vphantom{b}}+\overrightarrow{b}}{6}$
B. $\dfrac{2\overrightarrow{a\vphantom{b}}+\overrightarrow{b}}{3}$
C. $\dfrac{\overrightarrow{a\vphantom{b}}+2\overrightarrow{b}}{3}$
D. $\dfrac{\overrightarrow{a\vphantom{b}}+2\overrightarrow{b}}{2}$
E. $\overrightarrow{a\vphantom{b}}+\overrightarrow{b}$
$OACB$ квадратын $AC$ талын дундаж цэг $M$ ба $AB$ диагональ $OM$ хэрчимтэй $P$ цэгт огтлолцдог. Хэрэв $\overrightarrow{OA}=\overrightarrow{a\vphantom{OA}}$, $\overrightarrow{OB}=\overrightarrow{b\vphantom{OA}}$ бол $\overrightarrow{PM}$-ийг $\overrightarrow{a\vphantom{OA}}$, $\overrightarrow{b\vphantom{OA}}$-ээр илэрхийл.
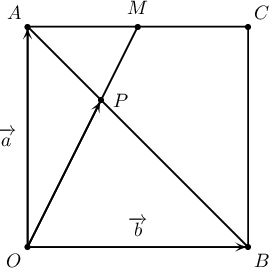

A. $\overrightarrow{a\vphantom{b}}+\overrightarrow{b}$
B. $\dfrac{2\overrightarrow{a\vphantom{b}}+\overrightarrow{b}}{2}$
C. $\dfrac{\overrightarrow{a\vphantom{b}}+2\overrightarrow{b}}{3}$
D. $\dfrac{\overrightarrow{a\vphantom{b}}+2\overrightarrow{b}}{2}$
E. $\dfrac{\overrightarrow{2a\vphantom{b}}+\overrightarrow{b}}{3}$
Векторын координат
$\vec{\mathstrut{a}}=(4, 2)$, $\vec{\mathstrut{b}}=(3,-1)$, $\vec{\mathstrut{x}}=(p, q)$ байв.
Хэрэв $\vec{\mathstrut{x}}\parallel(\vec{\mathstrut{a}}-\vec{\mathstrut{b}})$
ба $(\vec{\mathstrut{x}}-\vec{\mathstrut{b}})\perp\vec{\mathstrut{a}}$ бол $p, q$-г ол.
$\vec{\mathstrut{a}}=(3,-4)$ вектортой параллель, перпендикуляр байх нэгж векторуудыг ол.
$\vec{\mathstrut{u}}=(12,-5)$ вектортой эсрэг чиглэлтэй 2 нэгж урттай
векторыг ол.
$\vec{\mathstrut{a}}=(1, 1)$, $\vec{\mathstrut{b}}=(1, 3)$ векторууд өгөгдөв.
$\vec{\mathstrut{x}}+2\vec{\mathstrut{y}}=\vec{\mathstrut{a}}$, $\vec{\mathstrut{x}}-3\vec{\mathstrut{y}}=\vec{\mathstrut{b}}$
гэсэн нөхцлүүдийг хангах $\vec{\mathstrut{x}}$,
$\vec{\mathstrut{y}}$ векторуудыг ол.
$\vec{\mathstrut{a}}=(1,-2)$, $\vec{\mathstrut{b}}=(0, 3)$, $\vec{\mathstrut{c}}=(4,-3)$ бол
дараах векторуудын координат ба уртыг ол.
- $2\vec{\mathstrut{a}}-\vec{\mathstrut{b}}$
- $\vec{\mathstrut{a}}+\vec{\mathstrut{b}}-\vec{\mathstrut{c}}$
- $2\vec{\mathstrut{a}}-3\vec{\mathstrut{b}}+\vec{\mathstrut{c}}$
Координатын хавтгайд $O(0, 0)$, $A(7, 24)$, $B(3, 4)$+гурван
цэг авав. $\vec{\mathstrut{v}}$, $\vec{\mathstrut{w}}$ векторууд нь харгалзан
$\overrightarrow{OA}$, $\overrightarrow{OB}$-тэй ижил чиглэлтэй ба $\overrightarrow{OP}=\overrightarrow{OA}+t\vec{\mathstrut{v}}, t\in \mathbb R$
$\overrightarrow{OQ}=\overrightarrow{OB}+t\vec{\mathstrut{w}}$ гэе. Тэгвэл ${PQ}$ хэрчмийн дунджийг дайрах түүнд перпендикуляр шулуун $\dfrac lk$-ийн хувьд нэгэн утгатай болохыг харуул.
$\vec{\mathstrut{a}}=(-1, 1)$ вектортой $60^{\circ}$-ийн өнцөг үүсгэх нэгж векторыг ол.
$\vec{\mathstrut{a}}=(-3, 2)$, $\vec{\mathstrut{b}}=(2,-1)$ векторууд өгөгдөв. Дараах векторуудыг
$\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$ векторуудаар илэрхийл.
- $\vec{\mathstrut{c}}=(-3, 4)$
- $\vec{\mathstrut{d}}=(13,-10)$
$\vec{\mathstrut{a}}=(1, 2)$, $\vec{\mathstrut{b}}=(3, 1)$ векторууд
өгөгдөв. Хэрэв $\vec{\mathstrut{p}}=\vec{\mathstrut{a}}+t\cdot \vec{\mathstrut{b}}, t\in \mathbb R$
нөхцлийг хангах $\vec{\mathstrut{p}}$ векторын урт нь 5 нэгж бол
$t$-ийн утга болон $\vec{\mathstrut{p}}$-г ол.
$\vec{\mathstrut{a}}=(-1, 2)$, $\vec{\mathstrut{b}}=(2, 4)$ векторууд өгөгдөв.
Бодит тоо $t$-ийн хувьд $\vec{\mathstrut{c}}=\vec{\mathstrut{a}}+t\vec{\mathstrut{b}}$+векторын урт хамгийн бага байх $t\in\mathbb R$-г ол. Энэ үед $\vec{\mathstrut{c}}$-векторын урт хэд байх вэ?
$\vec{\mathstrut{a}}=(1, 1)$, $\vec{\mathstrut{b}}=(-1, 0)$, $\vec{\mathstrut{c}}=(1, 2)$ векторууд өгөгдөв. Хэрвээ $m$
$\vec{\mathstrut{c}}\parallel (m^2-3)\vec{\mathstrut{a}}+m\vec{\mathstrut{b}}$ нөхцлийг хангах натурал тоо бол $m$-ийн бүх боломжит утгыг ол.
Дараах $\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$ векторуудын скаляр үржвэрийг ол.
(1) $\vec{\mathstrut{a}}=(\sqrt{3}, 1)$,
$\vec{\mathstrut{b}}=(-1,-\sqrt{3})$ (2)
$\vec{\mathstrut{a}}=(1, 2), \vec{\mathstrut{b}}=(1,-3)$
(3) $\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$-ийн хоорондох
өнцөг нь $135^{\circ}$, $|\vec{\mathstrut{a}}|=\sqrt{6}$,
$\vec{\mathstrut{b}}=(-1, \sqrt{2})$.
$\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$ хоёр векторын хоорондох өнцгийг ол.
- $\vec{\mathstrut{a}}=(-1,-3)$, $\vec{\mathstrut{b}}=(6,-2)$
- $\vec{\mathstrut{a}}=(1, 1)$, $\vec{\mathstrut{b}}=(1-\sqrt{3}, 1+\sqrt{3})$
$(1;a;b)$, $(x;x;x)$, $x\not=0$ векторууд параллель бол $a+b=?$
A. 1
B. 2
C. 3
D. 4
E. 5
Дараах векторуудын аль нь нэгж вектор вэ?
A. $(1;1)$
B. $(1/2;1/2)$
C. $(\sin 36^\circ;-\sin 54^\circ)$
D. $(\log_23;1-\log_23)$
E. аль нь ч биш
$\vec{\mathstrut b}-\vec{\mathstrut a}=(3;2;5)$, $\vec{\mathstrut a}+\vec{\mathstrut b}=(1;4;-3)$ бол $\vec{\mathstrut a}, \vec{\mathstrut b}$-ийн скаляр үржвэр аль вэ?
A. $3$
B. $-3$
C. $-1$
D. $2$
E. $0$
Хоорондоо параллель байх векторууд аль нь вэ?
A. $\vec{\mathstrut a}=(1;2;0)$ ба $\vec{\mathstrut b}=(0;1;2)$
B. $\vec{\mathstrut a}=(-1;1;1)$ ба $\vec{\mathstrut b}=(1;1;1)$
C. $\vec{\mathstrut a}=(1;-1;1)$ ба $\vec{\mathstrut b}=(1;-2;1)$
D. $\vec{\mathstrut a}=(2;-1;1)$ ба $\vec{\mathstrut b}=(1;-1;2)$
E. $\vec{\mathstrut a}=(1;0;-2)$ ба $\vec{\mathstrut b}=(3;0;-6)$
Хоорондоо параллель байх векторууд аль нь вэ?
A. $\vec{\mathstrut a}=(-2;1;1)$ ба $\vec{\mathstrut b}=(2;1;1)$
B. $\vec{\mathstrut a}=(1;3;0)$ ба $\vec{\mathstrut b}=(0;1;3)$
C. $\vec{\mathstrut a}=(2;0;-1)$ ба $\vec{\mathstrut b}=(4;0;-2)$
D. $\vec{\mathstrut a}=(2;-1;0)$ ба $\vec{\mathstrut b}=(0;-1;2)$
E. $\vec{\mathstrut a}=(1;-1;1)$ ба $\vec{\mathstrut b}=(1;-2;1)$
$\vec{\mathstrut a}=(16;-4)$, $\vec{\mathstrut b}=(-4;1)$ векторууд аль нөхцөлийг хангах вэ?
A. $\vec{\mathstrut a}\uparrow\uparrow\vec{\mathstrut b}$
B. $\vec{\mathstrut a}\uparrow\downarrow\vec{\mathstrut b}$
C. $\vec{\mathstrut a}=-\vec{\mathstrut b}$
D. $\vec{\mathstrut a}\perp\vec{\mathstrut b}$
E. $\vec{\mathstrut a}=\vec{\mathstrut b}$
$\vec{\mathstrut a}=(4;-4)$, $\vec{\mathstrut b}=(-4;1)$ векторуудын скаляр үржвэр аль нь вэ?
A. $-20$
B. $-16$
C. $0$
D. $16$
E. $20$
$\vec{\mathstrut a}=(1;4)$, $\vec{\mathstrut b}=(-4;1)$ векторуудын скаляр үржвэр аль нь вэ?
A. $-10$
B. $-8$
C. $0$
D. $8$
E. $10$
$\vec{\mathstrut a}=(-4;6)$, $\vec{\mathstrut b}=(2;-3)$ векторууд аль нөхцөлийг хангах вэ?
A. $\vec{\mathstrut a}\perp\vec{\mathstrut b}$
B. $\vec{\mathstrut a}\uparrow\uparrow\vec{\mathstrut b}$
C. $\vec{\mathstrut a}=-\vec{\mathstrut b}$
D. $\vec{\mathstrut a}\uparrow\downarrow\vec{\mathstrut b}$
E. $\vec{\mathstrut a}=\vec{\mathstrut b}$
$f(x)=2x+a$ функц дээр $M(-1, 3)$ цэг оршдог бол $a$ тоог ол
A. $(3 )$
B. $( 4)$
C. $(5)$
D. $(6)$
E. $(7)$
$ |x-3|dx $ тодорхой интегралыг бодоорой.
A. $ \frac{3}{2} $
B. $ \frac{5}{2} $
C. $ -\frac{3}{2}$
D. $ 1 $
E. $ 3$
$\vec{\mathstrut a} = (-1,-2, 3)$ , $ \vec{\mathstrut b} = (1, -2, -3)$ бол $ \vec{\mathstrut a}- \vec{\mathstrut b} = ?$
A. $ (-2, 0 , 6) $
B. $ (0, -4, 0) $
C. $ (-2, 0, -6) $
D. $ (2, 0, -6) $
E. $ (2, -4, 2) $
$\vec{\mathstrut a}= (0, -1, -1)$, $\vec{\mathstrut b} = (1, -1, -2)$ векторуудын хоорондох өнцгийг олоорой.
A. $150^\circ $
B. $45^\circ $
C. $60 ^\circ $
D. $30^\circ $
E. $90 ^\circ $
$f(x)=2x+a$ функц дээр $M(-1, 3)$ цэг оршдог бол $a$ тоог ол
A. $(3 )$
B. $( 4)$
C. $(5)$
D. $(6)$
E. $(7)$
$\vec{\mathstrut a}= (0, -1, -1)$, $\vec{\mathstrut b} = (1, -1, -2)$ векторуудын хоорондох өнцгийг олоорой.
A. $120^\circ $
B. $45^\circ $
C. $60 ^\circ $
D. $30^\circ $
E. $90 ^\circ $
$ \vec{\mathstrut a}= (-2,-3, 4)$ , $ \vec{\mathstrut b} = (2, -3, -4)$ бол $\vec{\mathstrut a}- \vec{\mathstrut b} =?$
A. $ (-4, 0 , 8) $
B. $ (4, -4, 0) $
C. $ (-2, 6, -8) $
D. $ (4, 0, -6) $
E. $ (2, -4, 8) $
$\vec{\mathstrut a}= (-1, 0, -1)$, $\vec{\mathstrut b} = ( -1, 1, 2)$ векторуудын хоорондох өнцгийг олоорой.
A. $120^\circ $
B. $45^\circ $
C. $60 ^\circ $
D. $30^\circ $
E. $90 ^\circ $
$T\colon x^2+y^2=1$ тойрогт багтсан зөв таван өнцөгтийн оройнууд нь $A(1;0)$, $B(\cos\alpha_1;\sin\alpha_1)$, $C(\cos\alpha_2;\sin\alpha_2)$, $D(\cos(-\alpha_2);\sin(-\alpha_2))$, $E(\cos(-\alpha_1);\sin(-\alpha_1))$ ба $0< \alpha_1< \alpha_2< \pi$ бол
- $\alpha_1=\dfrac{\fbox{a}}{\fbox{b}}\pi$, $\alpha_2=\fbox{c}\alpha_1$ байна (2 оноо);
- $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}+\overrightarrow{OE}=(\fbox{d};\fbox{e})$ тул $\cos\alpha_1+\cos2\alpha_1=-\dfrac{\fbox{f}}{\fbox{g}}$ (3 оноо);
- Иймд $\fbox{h}\cos^2\alpha_1+\fbox{i}\cos\alpha_1-1=0$ болох ба $\alpha_1< \dfrac{\pi}{2}\Rightarrow \cos\alpha_1=\dfrac{\sqrt{\fbox{j}}-1}{4}$ байна (3 оноо).
$A(1;0)$, $B(4;4)$ бол $\overrightarrow{AB}=(\fbox{a},\fbox{b})$ байна. $AB$ хэрчмийн дундач цэгийн координат нь $C\Big(\dfrac{\fbox{c}}{2};\fbox{d}\Big)$ байна. $C$ цэгийг дайрсан $AB$-д перпендикуляр шулууны тэгшитгэл нь $\fbox{ef}x+\fbox{g}y-33=0$ байна.
Векторын уртыг координатаар олох
Векторын үйлдлүүд
$|\vec{\mathstrut{x}}-\vec{\mathstrut{y}}|=1$, $|2\vec{\mathstrut{y}}-\vec{\mathstrut{x}}|=2$,
$(\vec{\mathstrut{x}}-\vec{\mathstrut{y}})\perp (2\vec{\mathstrut{y}}-\vec{\mathstrut{x}})$ байг.
- $\vec{\mathstrut{x}}$, $\vec{\mathstrut{y}}$ векторуудын уртыг ол.
- $\vec{\mathstrut{x}}$, $\vec{\mathstrut{y}}$-ийн хоорондох өнцөг $\theta$ бол $\cos\theta$-г ол.
$\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}\ne 0$,
$\vec{\mathstrut{a}}\nparallel \vec{\mathstrut{b}}$ байг. $|2\vec{\mathstrut{a}}+t\vec{\mathstrut{b}}|$ нь хамгийн бага утга
авах үед $2\vec{\mathstrut{a}}+t\vec{\mathstrut{b}}$ ба
$\vec{\mathstrut{b}}$ векторуудын хоорондох өнцөг ямар байх вэ?
$ABC$ гурвалжны талуудын хувьд $AB:AC=1:4$ харьцаа биелэж байв. Хэрэв
$\overrightarrow{AF}=\dfrac 47\overrightarrow{AB}+\dfrac 17\overrightarrow{AC}$ ба $\measuredangle
BAF=30^{\circ}$ бол $\measuredangle BAC$-г ол.
Хавтгай дээрх $O$, $A$, $B$ гурван цэг нь
$|\overrightarrow{OA}|=|\overrightarrow{OA}+\overrightarrow{OB}|=|2\overrightarrow{OA}+\overrightarrow{OB}|=1$ нөхцлийг
хангана. Тэгвэл $|\overrightarrow{AB}|$ болон $S_{OAB}$-г тус тус ол.
$\triangle OAB$ нь $OA=5$, $OB=4$, $AB=6$ ба
$\overrightarrow{OA}=\vec{\mathstrut{a}}$, $\overrightarrow{OB}=\vec{\mathstrut{b}}$
байв. $AB$ талыг 2:1 харьцаанд хуваах $P$ цэгээс+$OA$ шулуунд
буулгасан перпендикулярын суурийг $Q$ гэе. Тэгвэл $\overrightarrow{PQ}$
векторыг $\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$ векторуудаар
илэрхийл.
Хавтгай дээрх $\vec{\mathstrut{a}}$,
$\vec{\mathstrut{b}}$ векторууд нь
$|3\vec{\mathstrut{a}}-2\vec{\mathstrut{b}}|=1$,
$|2\vec{\mathstrut{a}}+\vec{\mathstrut{b}}|=1$ нөхцлүүдийг хангаж
байв. Тэгвэл $\vec{\mathstrut{a}}\cdot \vec{\mathstrut{b}}$ скаляр үржвэрийн утгын мужийг ол.
$O$ төвтэй нэгж радиустай тойрог дээр $A$, $B$, $C$ гурван цэг өгөгдөв.
- Хэрэв $13\overrightarrow{OA}+12\overrightarrow{OB}+5\overrightarrow{OC}=\overrightarrow{0}$ бол $\overrightarrow{OB}\perp \overrightarrow{OC}$ гэж харуул.
- $4\overrightarrow{OA}+5\overrightarrow{OB}+6\overrightarrow{OC}=\vec{\mathstrut0}$ бол $|\overrightarrow{AB}|$-г ол.
$ABC$ гурвалжны $BC$ талыг $3:2$ харьцаанд хуваах
$P$ цэг, $AP$ хэрчмийг $3:2$ харьцаанд хуваах $Q$ цэг тус тус
өгөгдөв. $\overrightarrow{BQ}$-г $\overrightarrow{AB}$, $\overrightarrow{AC}$-ээр илэрхийл. Мөн
$QBC$ гурвалжны хүндийн төв нь $G$ бол $\overrightarrow{AG}$-г $\overrightarrow{AB}$,
$\overrightarrow{AC}$-ээр илэрхийл.
$ABC$ гурвалжны $BC$, $CA$, $AB$ талыг харгалзан
$m:n$ харьцаанд хуваах $P$, $Q$, $R$ цэгүүд өгөгдөв.
- $\overrightarrow{AP}+\overrightarrow{BQ}+\overrightarrow{CR}=\overrightarrow{0}$ болохыг батал.
- $ABC$ гурвалжны хүндийн төв нь $PQR$ гурвалжны хүндийн төвтэй давхцахыг батал.
$\ell$, $m$, $n$ натурал тоонууд бол
$\ell\overrightarrow{AP}+m\overrightarrow{BP}+n\overrightarrow{CP}=\overrightarrow{0}$ нөхцлийг хангах $P$ цэгийн
байршлыг тодорхойл.
$ABC$ гурвалжныг багтаасан тойргийн төв $O$ ба $H$
нь $\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$ байх цэг байв. Мөн $OH$,
$BC$, $CA$, $AH$ хэрчмүүдийн дундаж цэгүүд харгалзан $N$, $L$,
$M$, $D$ бол $N$ цэг дээр төвтэй $\dfrac 12|\overrightarrow{OA}|$ радиустай
тойрог дээр $L$, $M$, $D$ цэгүүд оршихыг батал.
$l>0$, $m>0$, $n>0$ бүхэл тоонууд байг. $ABC$ гурвалжин ба $P$ цэгийн
хувьд $$l\overrightarrow{AP}+m\overrightarrow{BP}+n\overrightarrow{CP}=\overrightarrow{0}$$ нөхцөл биелэх
зайлшгүй бөгөөд хүрэлцээтэй нөхцөл нь
$$S_{PBC}:S_{PCA}:S_{PAB}=l:m:n$$ болохыг батал.
$m$, $n$ эерэг бүхэл тоонууд ба $AB=AC$ байх адил хажуут $ABC$ гурвалжны
$AB$, $BC$, $CA$ талуудыг харгалзан $m:n$ харьцаанд хуваах $D$,
$E$, $F$ цэгүүд өгөгдөв.
- $\overrightarrow{AB}=\vec{\mathstrut{b}}$, $\overrightarrow{AC}=\vec{\mathstrut{c}}$ бол $\overrightarrow{AE}$, $\overrightarrow{DF}$-ыг $\vec{\mathstrut{b}}$, $\vec{\mathstrut{c}}$-ээр илэрхийл.
- $\overrightarrow{AE}\perp \overrightarrow{DF}$ байх нөхцлийг тогтоо.
$ABC$ гурвалжин өгөгдөв. $P$ цэг нь
$$2(2k+3)\overrightarrow{PA}+(3+k)\overrightarrow{PB}-(3+5k)\overrightarrow{PC}= \vec{\mathstrut{0}}$$
нөхцлийг хангана. (Энд $k$ нь дурын бодит тоо).
- $P$ цэгийн геометр байрыг ол.
- $P$ цэг нь $ABC$ гурвалжны дотоод мужид байх $k$-ийн утгын мужийг ол.
- $OXY$ координатын хавтгайд $OA=OB\ne 0$ байх ялгаатай $A$, $B$ цэгүүд өгөгдөв. $\overrightarrow{OA}=\vec{\mathstrut a}$, $\overrightarrow{OB}=\vec{\mathstrut{b}}$ бол $AOB$ өнцгийн биссектрис шулууны тэгшитгэл нь $(\vec{\mathstrut a}-\vec{\mathstrut{b}})\cdot \vec{\mathstrut{p}}=0$ болохыг харуул.
- $C(12, 5)$, $D(-3, 4)$ бол $COB$ өнцгийн биссектрисийн тэгшитгэлийг бич.
$\vec{\mathstrut{a}}\ne \vec{\mathstrut{0}}$, $\vec{\mathstrut{b}}\ne \vec{\mathstrut{0}}$, $\vec{\mathstrut{a}}\ne \vec{\mathstrut{b}}$ байх $A(\vec{\mathstrut{a}})$, $B(\vec{\mathstrut{b}})$
цэгүүд өгөгдөв. Дараах тэгшитгэлийг хангах $P(\vec{\mathstrut{p}})$ цэгийн геометр байрыг тодорхойл.
- $(2\vec{\mathstrut{p}}-\vec{\mathstrut a})\cdot (\vec{\mathstrut{p}}+2\vec{\mathstrut{b}})=0$
- $|\vec{\mathstrut{p}}-\vec{\mathstrut a}|=|\vec{\mathstrut{p}}-\vec{\mathstrut{b}}|$
- $|\vec{\mathstrut a}\cdot \vec{\mathstrut{p}}|=|\vec{\mathstrut a}|\cdot |\vec{\mathstrut{p}}|$
- $|3\vec{\mathstrut{p}}-2\vec{\mathstrut a}-\vec{\mathstrut{b}}|=|\vec{\mathstrut a}-\vec{\mathstrut{b}}|$
$\triangle ABC$ гурвалжны хувьд $\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}$ гэе. $s$, $t$-ийн хувьд дараах нөхцлийг хангах үед $P$ цэгийн геометр байрыг ол.
- $t=0$, $-1\leq s\leq 2$
- $s+t=2$
- $5s+2t=3$
- $0\leq s\leq 1$, $0\leq t\leq 1$
- $1< s+t< 2$
$A(\vec{\mathstrut{a}})$, $B(\vec{\mathstrut{b}})$, $C(\vec{\mathstrut{c}})$ байв.
$\triangle ABC$ гурвалжинд $AM$ медиан татав. $M$ цэгийг дайрах $BC$ талд
перпендикуляр шулууны вектор тэгшитгэлийг бич.
Хавтгайд $O$, $P$, $Q$, $R$ цэгүүд ба $ABCD$ параллельограмм өгөгдөв. Тэдгээр нь
$\overrightarrow{OP}=\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}$,
$\overrightarrow{OQ}=2\overrightarrow{OA}+3\overrightarrow{OB}+\overrightarrow{OC}$,
$\overrightarrow{OR}=3\overrightarrow{OA}+\overrightarrow{OB}+2\overrightarrow{OC}$ нөхцлүүдийг хангадаг байв.
- $QR$, $BD$ шулуунууд параллель болохыг харуул.
- $AB=AC$ бол $PR$, $BC$ шулуунууд перпендикуляр болохыг харуул.
$ABCDEF$ нь зөв зургаан өнцөгт бол $\overrightarrow{AB}=\vec{\mathstrut{a}}, $ $ \overrightarrow{BC}=\vec{\mathstrut{b}}$ векторуудыг $\overrightarrow{BD}=\vec{\mathstrut{d}}$, $\overrightarrow{BE}=\vec{\mathstrut{e}}$ векторуудаар илэрхийл.
$ABC$ гурвалжны $BC$, $CA$, $AB$ талууд дээр
харгалзан $D$, $E$, $F$ цэгүүдийг+$BD:DC=CE:EA=AF:FB=1:2$ харьцаа
биелэж байхаар авчээ. $\overrightarrow{CA}=\vec{\mathstrut{a}}$,
$\overrightarrow{CB}=\vec{\mathstrut{b}}$ бол дараах векторыг
- $\overrightarrow{AD}$
- $\overrightarrow{BE}$
- $\overrightarrow{CF}$
- $\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}$
$(2\vec{\mathstrut{a}}+3\vec{\mathstrut{b}})\parallel
(\vec{\mathstrut{a}}-4\vec{\mathstrut{b}})$ ба
$\vec{\mathstrut{a}}\ne \vec{\mathstrut{0}}$,
$\vec{\mathstrut{b}}\ne \vec{\mathstrut{0}}$ бол
$\vec{\mathstrut{a}}\parallel \vec{\mathstrut{b}}$ болохыг батал.
$AB=3$, $AD=4$ байх $ABCD$ тэгш өнцөгт өгөгдөв.
$\overrightarrow{AB}=\vec{\mathstrut{b}}$, $\overrightarrow{AD}=\vec{\mathstrut{d}}$ бол
дараах вектортэй параллель нэгж векторыг $\vec{\mathstrut{b}}$,
$\vec{\mathstrut{d}}$ векторуудаар илэрхийл.
- $\overrightarrow{BD}$
- $\overrightarrow{AB}+\overrightarrow{AC}$
Өмнөх жишээ бодлогод өгөгдсөн $\vec{\mathstrut{a}}$,
$\vec{\mathstrut{b}}$, $\vec{\mathstrut{c}}$ гурван векторыг
ашиглан $\vec{\mathstrut{a}}+2\vec{\mathstrut{b}}$,
$2\vec{\mathstrut{a}}-\vec{\mathstrut{b}}$,
$2\vec{\mathstrut{a}}-\vec{\mathstrut{b}}+3\vec{\mathstrut{c}}$
векторуудыг тус тус зургаар илэрхийл.
$ABCDEF$ зөв зургаан өнцөгтийн оройнууд дээр эхлэл,
төгсгөлтэй векторуудын хувьд:
- $\overrightarrow{AB}$ вектортой ижил чиглэлтэй;
- $\overrightarrow{EF}$ вектортой эсрэг чиглэлтэй;
- $\overrightarrow{AC}$ вектортой ижил чиглэлтэй;
- $\overrightarrow{AB}$ вектортой тэнцүү
Хавтгайд нэгж талтай $ABC$ зөв гурвалжин өгөгдөв. $|\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}|=|\overrightarrow{PA}-3\overrightarrow{PB}+2\overrightarrow{PC}|$ нөхцлийг хангах $P$ цэгийн геометр байрыг ол.
Хавтгай дээр $ABCD$ параллелограмм авав. Түүний диагоналын огтлолцлын цэгийг $E$ гэе. Уг хавтгай дээр орших $P$, $Q$, $R$ цэгүүдийн хувьд
- $\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}$, $s+2t\leq 1$, $s\geq 0$, $t\geq 0$ байх $P$+цэгийн,
- $\overrightarrow{AQ}+\overrightarrow{BQ}+\overrightarrow{CQ}=u\cdot \overrightarrow{DQ}$ байх $Q$+цэгийн,
- $(\overrightarrow{ER}+\overrightarrow{EA})\cdot (\overrightarrow{ER}-\overrightarrow{EA})=0$ байх $R$ цэгийн геометр байрыг тус тус тодорхойл.
Хавтгай дээрх $O$, $A$, $B$, $C$ дөрвөн цэгийн хувьд
$$\overrightarrow{CA}+2\overrightarrow{CB}+3\overrightarrow{CO}=\vec{\mathstrut{0}}$$ тэнцэл биелэнэ. $A$ ба $B$ цэгүүд нь $O$ дээр төвтэй $12$ радиустай тойрог дээр орших цэг бол $C$ цэгийн геометр байрыг ол.
$OXY$ координатын хавтгайд $A(1, 2)$, $B(3,-1)$ цэгүүд авав. Тэгвэл
$\overrightarrow{OP}=\alpha\overrightarrow{OA}+\beta\overrightarrow{OB}$, $-1\leq \alpha\leq 1$,
$-1\leq \beta\leq 1$, $0\leq \alpha+\beta\leq 1$ нөхцлийг хангах
$P$ цэгийн геометр байрыг ол.
$OABC$ параллелограммийн $AB$ талыг $2:3$ харьцаанд хуваах $D$, $AC$ диагоналыг $2:5$ харьцаанд хуваах $E$ цэгүүд байв. $O$, $E$, $D$ цэгүүд нэг шулуун дээр оршихыг харуул.
$OAB$ гурвалжны $AB$ тал дээр $AC:CD:DB=2:3:1$ харьцаа биелэх $C$, $D$ цэгүүдийг
авав. $OA$ тал болон $OD$, $BP$ хэрчмүүдийн дундаж цэгүүд харгалзан $P$, $Q$, $R$ бол $OC\parallel QR$ болохыг батал.
Дээрх жишээ бодлогын хувьд $OP$, $CD$-ийн огтлолцлыг $Q$ гэе.
$\overrightarrow{OQ}$ векторыг $\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$-ээр илэрхийл.
$ABC$ гурвалжны $AB$ талыг $2:1$ харьцаанд хуваах цэгийг $L$, $AC$ талын дундаж цэгийг $M$ гэе. $CL$, $BM$ хэрчмүүд $P$ цэгт, $AP$ шулуун $BC$ хэрчимтэй $N$ цэгт огтлолцдог байг. Тэгвэл $\overrightarrow{AP}$, $\overrightarrow{AN}$ векторуудыг $\overrightarrow{AB}$, $\overrightarrow{AC}$ векторуудаар илэрхийл.
$ABCD$ параллельограммын $AB$, $BC$ талуудыг
харгалзан $m:n$, $3:2$ харьцаанд хуваах цэгүүдийг $E$, $F$ гэе.
Мөн $AF$, $DE$ хэрчмүүд болон $AC$, $BD$ диагоналиудын огтлолцлын
цэгүүд харгалзан $P$, $Q$ байг. $\overrightarrow{AB}=\vec{\mathstrut{a}}$,
$\overrightarrow{AD}=\vec{\mathstrut{b}}$ бол
- $\overrightarrow{AP}$ векторыг+$\vec{\mathstrut{a}}, \vec{\mathstrut{b}}, m, n$-ээр илэрхийл.
- $\overrightarrow{PQ}\parallel \overrightarrow{AD}$ байх үед $m:n$ харьцааг+ол.
$ABC$ гурвалжны $BC$, $CA$, $AB$ талууд дээр харгалзан $D$, $E$, $F$ цэгүүдийг авав.
$\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\vec{\mathstrut{0}}$ нөхцөл биелэх үед
$BD:DC=CE:EA=AF:FB$ болохыг батал.
$OAB$ гурвалжны гадна талд $OACD$, $OBEF$
квадратууд байгуулав. Мөн $ODGF$ нь параллелограмм байхаар $G$
цэгийг сонгов. Тэгвэл $OG\perp AB$ болохыг батал.
$OXY$ координатын хавтгайд координатын эхийг дайрах $l$ шулуун ба түүнд перпендикуляр нэгж вектор $\vec{\mathstrut{e}}$-г тус тус авъя. $A(\vec{\mathstrut{a}})$, $B(\vec{\mathstrut{b}})$ цэгүүд $l$ шулууны хувьд тэгш
хэмтэй бол $\vec{\mathstrut{b}}=\vec{\mathstrut{a}}-2(\vec{\mathstrut{a}}\cdot \vec{\mathstrut{e}})\cdot \vec{\mathstrut{e}}$
болохыг харуул.
$ABC$ гурвалжны хүндийн төв $G$, орто төв $H$,
багтаасан тойргийн төв $O$ байг. $\overrightarrow{OA}=\vec{\mathstrut{a}}$,
$\overrightarrow{OB}=\vec{\mathstrut{b}}$, $\overrightarrow{OC}=\vec{\mathstrut{c}}$ бол
$3\overrightarrow{OG}=\vec{\mathstrut{a}}+\vec{\mathstrut{b}}+\vec{\mathstrut{c}}$,
$\overrightarrow{OH}=\vec{\mathstrut{a}}+\vec{\mathstrut{b}}+\vec{\mathstrut{c}}$ болохыг тус тус батал.
$O$ цэгт төвтэй тойрогт багтсан $ABC$ гурвалжны хувьд $AB=2$,
$AC=3$, $\measuredangle A=60^{\circ}$ байв. $\overrightarrow{AB}=\vec{\mathstrut{b}}$,
$\overrightarrow{AC}=\vec{\mathstrut{c}}$ гэвэл $\overrightarrow{AO}$-г $\vec{\mathstrut{b}}$, $\vec{\mathstrut{c}}$-ээр
илэрхийл.
$OAB$ гурвалжны $OA$ талыг $s:(1-s)$ харьцаанд
хуваах $P$, $OB$ талыг $t:(1-t)$ харьцаанд хуваах $Q$ цэгүүдийг
тус тус авъя. $BP$, $AQ$ хэрчмүүд $R$ цэгт огтлолцдог ба $OR$-ийн
үргэлжлэл $AB$-тэй $S$ цэгээр огтлолцдог байв.
- $\overrightarrow{OR}$-ыг $\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$, $s$, $t$-ээр илэрхийл.
- $OS$ нь $\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$, $s$, $t$-ээр илэрхийл.
- $S$ нь $AB$ талын дундаж байх нөхцлийг тодорхойл.
$AB=4$, $CA=3$, $\measuredangle BAC=90^{\circ}$
байх $ABC$ гурвалжинд багтсан тойргийн төв $I$ байв. $OI=\alpha\overrightarrow{OA}+\beta\overrightarrow{OB}+\gamma\overrightarrow{OC}$ үед $\alpha$,
$\beta$, $\gamma$-г ол.
$A$ цэгийг координатын эхлэл $O$ цэгт төвтэй
$\theta$ $(0^{\circ}\leq \theta\leq 360^{\circ})$ өнцгөөр
эргүүлэхэд $\vec{\mathstrut{a}}$-вектороор шилжиж $P$ цэг үүсэв. Гарсан $P$
цэгийг дахин $\theta$ өнцгөөр эргүүлж $Q$ цэг үүсгэв.
- $A(1, 0)$ үед $P(1, 1)$ байх $Q$ болон $|\vec{\mathstrut{a}}|$-ын хамгийн бага утгыг ол.
- $|\vec{\mathstrut{a}}|=l$, $PQ=d$ үед $d\leq 2l$ болохыг харуул.
$ABCDEF$ зөв зургаан өнцөгтийн талын урт 2 нэгж байв. Тэгвэл $\overrightarrow{AB}\cdot \overrightarrow{AF}$, $\overrightarrow{AB}\cdot \overrightarrow{AC}$,
$\overrightarrow{AD}\cdot \overrightarrow{BE}$-г тус тус ол.
Батал.
- [(A)] $|\vec{\mathstrut{a}}+\vec{\mathstrut{b}}+\vec{\mathstrut{c}}|^2+|\vec{\mathstrut{a}}|^2+|\vec{\mathstrut{b}}|^2+|\vec{\mathstrut{c}}|^2=|\vec{\mathstrut{a}}+\vec{\mathstrut{b}}|^2+|\vec{\mathstrut{b}}+\vec{\mathstrut{c}}|^2+|\vec{\mathstrut{c}}+\vec{\mathstrut{a}}|^2.$
- [(B)] (1) $|\vec{\mathstrut{a}}\cdot \vec{\mathstrut{b}}|\leq |\vec{\mathstrut{a}}|\cdot |\vec{\mathstrut{b}}|$ (2) $|\vec{\mathstrut{a}}|-|\vec{\mathstrut{b}}|\leq |\vec{\mathstrut{a}}+\vec{\mathstrut{b}}|\leq |\vec{\mathstrut{a}}|+|\vec{\mathstrut{b}}|.$
$\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$ векторууд
$|\vec{\mathstrut{a}}|=1$, $|\vec{\mathstrut{b}}|=2$,
$|\vec{\mathstrut{a}}+2\vec{\mathstrut{b}}|=3$ нөхцөлүүдийг хангах
бол $|\vec{\mathstrut{a}}-2\vec{\mathstrut{b}}|$ -ын утгыг ол.
$\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$, $\vec{\mathstrut{c}}$ нь дараах нөхцөлийг хангах үед
$\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$-ийн хоорондох өнцөг $\theta$-г ол.
-
$|\vec{\mathstrut{a}}|=3, |\vec{\mathstrut{b}}|=5, |\vec{\mathstrut{a}}+\vec{\mathstrut{b}}|=7$
- $\vec{\mathstrut{a}}+\vec{\mathstrut{b}}+\vec{\mathstrut{c}}=\vec{\mathstrut{0}}$ ба $|\vec{\mathstrut{a}}|=|\vec{\mathstrut{b}}|=|\vec{\mathstrut{c}}|=1$
(1) $3\vec{\mathstrut{x}}+\vec{\mathstrut{a}}=5\vec{\mathstrut{x}}-2\vec{\mathstrut{b}}$-г
хангах $\vec{\mathstrut{x}}$-ыг $\vec{\mathstrut{a}}$,
$\vec{\mathstrut{b}}$-ээр илэрхийл.
(2) $3\vec{\mathstrut{x}}+2\vec{\mathstrut{y}}=\vec{\mathstrut{a}}$,
$2\vec{\mathstrut{x}}-3\vec{\mathstrut{y}}=\vec{\mathstrut{b}}$ -г хангах
$\vec{\mathstrut{x}}$, $\vec{\mathstrut{y}}$-ыг $\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$-ээр илэрхийл.
Дараах тэнцэтгэлийг батал.
- $\overrightarrow{PQ}+\overrightarrow{RP}=\overrightarrow{RQ}$
- $\overrightarrow{AD}+\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{BD}$
$\vec{\mathstrut{x}}=2\vec{\mathstrut{a}}+5\vec{\mathstrut{b}}-\vec{\mathstrut{c}}$,
$ \vec{\mathstrut{y}}=3\vec{\mathstrut{a}}-\vec{\mathstrut{b}}+2\vec{\mathstrut{c}}$
бол $\vec{\mathstrut{x}}+\vec{\mathstrut{y}}, 2\vec{\mathstrut{x}}-3\vec{\mathstrut{y}}$ векторуудыг $\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$, $\vec{\mathstrut{c}}$-ээр илэрхийл.
Нэгж талтай зөв таван өнцөгт $ABCDE$-ийн хувьд
$\overrightarrow{AB}=\vec{\mathstrut{a}}$, $\overrightarrow{AE}=\vec{\mathstrut{b}}$ ба $BE$ хэрчмийн уртыг $t$
гэе.
- $\overrightarrow{CD}$-г $\vec{\mathstrut{a}}, \vec{\mathstrut{b}}, t$-ээр илэрхийл.
- $\overrightarrow{DE}$-г $\vec{\mathstrut{a}}, \vec{\mathstrut{b}}, t$-ээр илэрхийл.
- $\overrightarrow{BC}$-г $\vec{\mathstrut{a}}, \vec{\mathstrut{b}}, t$-ээр хоёр янзаар илэрхийлж, $t$-ийн утгыг ол.
Координатын хавтгайд $A(0, \sqrt{3})$, $B(-1, 0)$, $C(2, 0)$
цэгүүдийг авъя. $ABC$ өнцгийн биссектрис нь $AC$ хэрчмийг $D$
цэгээр огтолно.
- $AD:DC$ харьцаа болон $\overrightarrow{BD}$-г тус тус ол.
- $l$ шулуун дээр $Q$, $R$ хоёр цэгийг харгалзан $ABC$ гурвалжны дотор болон гадна талд байхаар авах ба $\measuredangle AQC=\measuredangle ARC=90^{\circ}$ үед $\overrightarrow{BQ}$, $\overrightarrow{BR}$ векторуудыг ол.
- Энэ үед $QD:DR$ болон $S_{AQD}:S_{CRD}$ харьцааг тус тус ол.
$OA=3$, $OB=4$, $AB=\sqrt{19}$ байх $OAB$ гурвалжны $OB$ тал
дээр $OP=3$ байх $P$ цэг авчээ. Мөн гурвалжны хавтгайд $OAB$,
$OPQ$ нь тэнцүү гурвалжнууд байх $Q$ цэг авав.
- $\measuredangle AOB=\theta$ гэвэл $\cos \theta$-г ол.
- $\overrightarrow{OA}\cdot \overrightarrow{OQ}$-ийн утгыг ол.
- $\overrightarrow{OQ}=m\cdot \overrightarrow{OA}+n\cdot \overrightarrow{OB}$ байх $m, n$-бодит тоонуудыг ол.
$ABC$ гурвалжныг багтаасан тойргийн төв $O$ ба радиус нь
$\sqrt{3}$ байв. $\overrightarrow{OA}$, $\overrightarrow{OB}$, $\overrightarrow{OC}$-ийн хувьд
$17\overrightarrow{OA}+15\overrightarrow{OB}+8\overrightarrow{OC}=\vec{\mathstrut{0}}$ нөхцлийг хангах үед
- $\overrightarrow{OB}\perp \overrightarrow{OC}$ болохыг харуул.
- $OAB$, $OBC$, $OCA$ гурвалжнуудын талбайг ол.
- $A$ оройгоос татсан өндрийг ол.
$ABC$ гурвалжны $BC$ талыг 2:1 харьцаагаар хуваах $D$ цэг
авав. $AD$ хэрчим дээрх $P$ цэгийн хувьд
$4\overrightarrow{PA}+\overrightarrow{PB}+s\overrightarrow{PC}=\vec{\mathstrut{0}}$ нөхцөл биелэх бол
- $s$-ийн утгыг ол. $\overrightarrow{AP}$-г $\overrightarrow{AB}$, $\overrightarrow{AC}$-ээр илэрхийл.
- $BP$ хэрчмийн дундаж $M$ болон $AB$, $BC$ тал дээр харгалзан $Q$, $R$ цэгүүийг авахад $\overrightarrow{AQ}=u\overrightarrow{AB}$, $\overrightarrow{BR}=\dfrac 12\overrightarrow{BC}$ бол $Q$, $M$, $R$ цэгүүд нэг шулуун дээр орших $u$-ийн утгыг ол.
$A(1, 0)$ цэгийг координатын эх $O$ цэгийн хувьд
$120^{\circ}$-аар эргүүлэхэд $B$ цэг, мөн $B$ цэгийг $O$ цэгийн
хувьд дахин $120^{\circ}$-аар эргүүлэхэд $C$ цэг гардаг байг.
$t\in\mathbb R$-г $0\leq t\leq 1,4$ үед $\overrightarrow{OP}=t^2\overrightarrow{OC}$ байх
$P$ цэгийг авъя.
- $ABP$ гурвалжны хүндийн төв $G$-ийн координатыг ол.
- $\overrightarrow{OG}$-ийн уртыг $t$-ээр илэрхийл. Энэ үед $|\overrightarrow{OG}|$-ийн хамгийн их утгыг ол.
$ABC$ гурвалжны $AB$, $BC$ талыг харгалзан $t:(1-t)$
харьцаанд хуваах $P$, $Q$ цэгийг авъя. (Энд $0< t< 1$).
$AC$ талын дундаж $M$ ба $PQ$, $BM$ шулуунууд $M$ цэгээр огтлолцох үед $\dfrac{BR}{BM}$-ыг $t$-ээр илэрхийл.
Дараах тэнцлийг хангах $ABC$ гурвалжны хэлбэрийг тогтоо.
- $\overrightarrow{AB}\cdot \overrightarrow{AB}=\overrightarrow{AB}\cdot \overrightarrow{AC}+\overrightarrow{BA}\cdot \overrightarrow{BC}+\overrightarrow{CA}\cdot \overrightarrow{CB}.$
- $(\overrightarrow{DB}-\overrightarrow{DC})\cdot (\overrightarrow{DB}+\overrightarrow{DC}-2\overrightarrow{DA})=0.$
Хавтгайд урт нь тэнцүү, аль ч хоёрынх нь хоорондох өнцөг
$120^{\circ}$ байх $\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$, $\vec{\mathstrut{c}}$ векторууд
өгөгдөв. Мөн уг хавтгайд дурын $\vec{\mathstrut{x}}$ вектор авъя.
- $\vec{\mathstrut{a}}+\vec{\mathstrut{b}}+\vec{\mathstrut{c}}=\vec{\mathstrut{0}}$ болохыг харуул.
- $\vec{\mathstrut{a}}\cdot \vec{\mathstrut{x}}+\vec{\mathstrut{b}}\cdot \vec{\mathstrut{x}}+\vec{\mathstrut{c}}\cdot \vec{\mathstrut{x}}=\vec{\mathstrut{0}}$ болохыг харуул.
- $\left\{(\vec{\mathstrut{a}}+\vec{\mathstrut{b}})\cdot \vec{\mathstrut{x}}\right\}^2+\left\{(\vec{\mathstrut{b}}+\vec{\mathstrut{c}})\cdot \vec{\mathstrut{x}}\right\}^2+\left\{(\vec{\mathstrut{c}}+\vec{\mathstrut{a}})\cdot \vec{\mathstrut{x}}\right\}^2$-ыг $|\vec{\mathstrut{a}}|$, $|\vec{\mathstrut{x}}|$-аар илэрхийл.
$m, n, r, t, u\in\mathbb R$ байг. Дурын $\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$
хоёр векторын хувьд $S(\vec{\mathstrut{a}},\vec{\mathstrut{b}})$-г
$S(\vec{\mathstrut{a}},\vec{\mathstrut{b}})=\sqrt{|\vec{\mathstrut{a}}|^2\cdot |\vec{\mathstrut{b}}|^2-(\vec{\mathstrut{a}}\cdot
\vec{\mathstrut{b}})^2}$ гэж тодорхойлъё.
- $S(m\vec{\mathstrut{a}},n\vec{\mathstrut{b}})$-г $m, n, S(\vec{\mathstrut{a}},\vec{\mathstrut{b}})$-ээр илэрхийл.
- $S(\vec{\mathstrut{a}},r\vec{\mathstrut{a}}+\vec{\mathstrut{b}})$-ыг $r$, $S(\vec{\mathstrut{a}},\vec{\mathstrut{b}})$-ээр илэрхийл.
- $S(t\vec{\mathstrut{a}}+u\vec{\mathstrut{b}},-u\vec{\mathstrut{a}}+t\vec{\mathstrut{b}})$-ыг $t$, $u$, $S(\vec{\mathstrut{a}},\vec{\mathstrut{b}})$-ээр илэрхийл.
Хавтгайд аль ч хоёр нь параллель биш тэгээс ялгаатай
$\vec{\mathstrut{a}}_1$, $\vec{\mathstrut{a}}_2$ $\vec{\mathstrut{a}}_3$ векторуудын хувьд
$\vec{\mathstrut{a}}_1+\vec{\mathstrut{a}}_2+\vec{\mathstrut{a}}_3=\vec{\mathstrut{0}}$ нөхцөл биелэнэ. Уг хавтгайн
дурын тэгээс ялгаатай векторыг $\vec{\mathstrut{x}}$ гэе. Тэгвэл $\vec{\mathstrut{x}}\cdot
\vec{\mathstrut{a}}_i>0$, $\vec{\mathstrut{x}}\cdot \vec{\mathstrut{a}}_{i+1}\leq 0$ $(i=1, 2, 3)$
нөхцлийг хангах $\vec{\mathstrut{x}}$ вектор нь зөвхөн ганц болохыг батал. Энд
$(\vec{\mathstrut{a}}_1=\vec{\mathstrut{a}}_4).$
Хавтгайн $ABCD$ параллельограмм болон $P$ цэгийн хувьд $m\overrightarrow{AP}+\overrightarrow{BP}+\overrightarrow{CP}=\vec{\mathstrut{0}}$ $(m>0)$ хангана.
- $\overrightarrow{AB}=\vec{\mathstrut{u}}$, $\overrightarrow{AC}=\vec{\mathstrut{v}}$ бол $\overrightarrow{AP}$ векторыг $\vec{\mathstrut{u}}$, $\vec{\mathstrut{v}}$, $m$-ээр илэрхийл.
- $AP$ шулуун $BC$ талтай $Q$ цэгээр огтлолцох $AP:PQ$ харьцааг $m$-ээр илэрхийл.
- $ACD$ гурвалжны хүндийн төв $G$ ба $PG$ хэрчим нь $AD$ талтай параллель байх $m$-ийн утгыг ол.
$OXY$ Координатын хавтгайд өгөгдсөн $A(1, 3)$, $B(2, 7)$
цэгүүдийн $Ox$ тэнхлэгийн хувьд тэгш хэмтэй цэгүүд нь харгалзан
$C$, $D$ байг. Дурын $P(x, y)$ цэгийн радиус вектор $\overrightarrow{OP}$ нь
$\overrightarrow{OP}=\alpha\overrightarrow{OA}+\beta\overrightarrow{OB} \boldsymbol{\cdots}(1)$ бол
- $\overrightarrow{OC}$, $\overrightarrow{OD}$-г тус тус (1) хэлбэрээр илэрхийл.
- $P$ цэг нь $AB$ хэрчим дээр байх $\alpha$, $\beta$-ийн нөхцлийг тодорхойл.
- $P$ цэг нь $CD$ хэрчим дээр байх $\alpha$, $\beta$-ийн нөхцлийг тодорхойл.
- $P$ цэг нь $OCD$ гурвалжин дээр болон түүний дотор орших $\alpha$, $\beta$-ийн нөхцлийг тодорхойл.
$OAB$ гурвалжны $OA$, $OB$ талууд дээр харгалзан $P$, $Q$
цэгүүд хөдөлж байв. $2\overrightarrow{OP}\cdot \overrightarrow{OB}+2\overrightarrow{OQ}\cdot
\overrightarrow{OA}=3\overrightarrow{OA}\cdot \overrightarrow{OB}$ нөхцөл биелэх үед $OPQ$ гурвалжны
хүндийн төв $G$-ийн геометр байрыг зургаар дүрсэл.
$OAB$ гурвалжны $OA$, $AB$, $BO$ талуудыг харгалзан $t:(1-t)$ харьцаанд
хуваах $P$, $Q$, $R$ цэгүүд өгөгдөв. (Энд $t$ нь $0< t< 1$ байна).
$\overrightarrow{OA}=\vec{\mathstrut{a}}$, $\overrightarrow{OB}=\vec{\mathstrut{b}}$ үед $\overrightarrow{PQ}$, $\overrightarrow{PR}$-г $t$, $\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$-аар илэрхийл.
$\dfrac{|\overrightarrow{PQ}|}{|\overrightarrow{PR}|}=\dfrac{|\vec{\mathstrut{b}}|}{|\vec{\mathstrut{a}}|}$ нөхцөл+дурын $t$-ийн хувьд биелэх үед $OAB$ гурвалжны хэлбэрийг тогтоо.
$OXY$ хавтгайд $\vec{\mathstrut{a}}=(\cos\theta,\sin \theta)$,
$\vec{\mathstrut{b}}=\left(\dfrac{\sqrt{3}}{2}, \dfrac 12\right)$ векторууд өгөгдөв.
$P_n$, $Q_n$, $n=1, 2,\ldots$ цэгүүдийг $\overrightarrow{OP}_1=(1, 0)$,
$\overrightarrow{OQ}_n=\overrightarrow{OP}_n-(\vec{\mathstrut{a}}\cdot \overrightarrow{OP}_n)\cdot \vec{\mathstrut{a}}$,
$\overrightarrow{OP}_n=4\left\{\overrightarrow{OQ}_n-(\vec{\mathstrut{b}}\cdot \overrightarrow{OQ}_n)\cdot
b\right\}$ гэсэн рекуррент томъёогоор тодорхойлъё. Тэгвэл
$P_1, P_2, P_3,\ldots$ цэгүүд нэг шулуун дээр, мөн $Q_1, Q_2, Q_3,\ldots$
цэгүүд нэг шулуун дээр оршихыг харуул.
Зурагт $\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$,
$\vec{\mathstrut{c}}$ гурван векторыг дүрслэв. Дараах векторуудыг
зургаар дүрсэл.
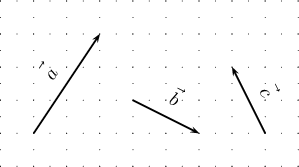
- $\vec{\mathstrut{a}}+\vec{\mathstrut{c}}$
- $\vec{\mathstrut{b}}-\vec{\mathstrut{c}}$
- $2\vec{\mathstrut{a}}$
- $-3\vec{\mathstrut{b}}$
- $\vec{\mathstrut{a}}+3\vec{\mathstrut{b}}-2\vec{\mathstrut{c}}$

- Хялбарчил.
- $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}$
- $\overrightarrow{AB}-\overrightarrow{CD}-\overrightarrow{AC}+\overrightarrow{BD}$
- $2(\vec{\mathstrut{a}}+3\vec{\mathstrut{b}})-3(\vec{\mathstrut{a}}-2\vec{\mathstrut{b}})$
- Дараах системээс $\vec{\mathstrut{x}}$, $\vec{\mathstrut{y}}$-г $\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$-ээр илэрхийл. $$\left\{ \begin{array}{cl} 3\vec{\mathstrut{x}}+\vec{\mathstrut{y}}=\vec{\mathstrut{a}} &\boldsymbol{\cdots}(1)\\5\vec{\mathstrut{x}}+2\vec{\mathstrut{y}}=\vec{\mathstrut{b}} & \boldsymbol{\cdots}(2) \end{array} \right.$$
Хавтгай дээр ялгаатай $A$, $B$, $C$, $D$,
$O$ цэгүүд байв. $\overrightarrow{OA}=\vec{\mathstrut{a}}$,
$\overrightarrow{OB}=\vec{\mathstrut{b}}$ ба
$\overrightarrow{OC}=3\vec{\mathstrut{a}}-2\vec{\mathstrut{b}}$,
$\overrightarrow{OD}=-3\vec{\mathstrut{a}}+4\vec{\mathstrut{b}}$ бол
$\overrightarrow{AB}\parallel \overrightarrow{CD}$ гэж харуул.
$ABCDEF$ нь зөв зургаан өнцөгт ба
$\overrightarrow{AB}=\vec{\mathstrut{a}}$, $\overrightarrow{AF}=\vec{\mathstrut{b}}$
байв. $\overrightarrow{BC}$, $\overrightarrow{EF}$, $\overrightarrow{CE}$, $\overrightarrow{AC}$, $\overrightarrow{BD}$,
$\overrightarrow{AD}$ векторуудыг $\vec{\mathstrut{a}}$,
$\vec{\mathstrut{b}}$-ээр илэрхийл.
$ABCD$ параллелограммын диагоналиудын
огтлолцлын цэгийг $E$, $BC$ талыг $2:1$ харьцаанд хуваах цэгийг $F$ гэе. $\overrightarrow{AB}=\vec{\mathstrut{b}}$,
$\overrightarrow{AD}=\vec{\mathstrut{d}}$ векторуудыг
$\overrightarrow{AE}=\vec{\mathstrut{e}}$, $\overrightarrow{AF}=\vec{\mathstrut{f}}$
векторуудаар илэрхийл.
- $\vec{\mathstrut{a}}=(-3, 2)$, $\vec{\mathstrut{b}}=(1, 1)$ векторууд өгөгдөв. $2\vec{\mathstrut{a}}-3\vec{\mathstrut{b}}$ векторыг координатаар илэрхийл. Мөн уг векторын уртыг ол.
- $\vec{\mathstrut{p}}=(-7, 2)$, $\vec{\mathstrut{x}}=(1, a)$, $\vec{\mathstrut{y}}=(b, 2)$ ба $\vec{\mathstrut{p}}=2\vec{\mathstrut{x}}-3\vec{\mathstrut{y}}$ нөхцлийг хангах $a, b$ тоонуудыг ол.
- $\vec{\mathstrut{u}}=(3,-4)$ вектортой параллел нэгж векторыг ол.
$\vec{\mathstrut{a}}=(1, 2)$,
$\vec{\mathstrut{b}}=(2, 1)$ ба $\vec{\mathstrut{c}}=(11, 10)$
байв. Хэрэв $\vec{\mathstrut{c}}$
вектор нь $\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$ векторуудаар
$\vec{\mathstrut{c}}=x\vec{\mathstrut{a}}+y\vec{\mathstrut{b}}, (x, y\in\mathbb R)$
гэж илэрхийлэгдэх бол $x, y$-ийг ол.
$A(1, 3)$, $B(3,-2)$, $C(4, 1)$ гэсэн гурван цэг өгөгдөв.
- $\overrightarrow{AB}$, $\overrightarrow{BA}$, $\overrightarrow{BC}$ векторуудын координатыг ол.
- $P(5, q)$ цэгийн хувьд $\overrightarrow{BP}=k\cdot \overrightarrow{BC}$ үед $k, q$-ийн утгыг ол.
- $ABCD$ дөрвөн өнцөгт нь параллельограмм байх $D$ цэгийн координатыг ол.
$\vec{\mathstrut{a}}=(-3, 2)$, $\vec{\mathstrut{b}}=(2, 1), \vec{\mathstrut{c}}=(3,-1)$ векторууд өгөгдөв. $|\vec{\mathstrut{a}}+t\vec{\mathstrut{b}}|$ нь хамгийн бага байх $t$-ийн утга нь $t=\ebox$ байна. Энэ үед $|\vec{\mathstrut{a}}+t\vec{\mathstrut{b}}|=\ebox$
байна. Түүнчлэн $t=\ebox$ үед $\vec{\mathstrut{a}}+t\vec{\mathstrut{b}}$ ба
$\vec{\mathstrut{c}}$ векторууд параллель байна.
- $AB=AC=2$, $\measuredangle B=30^{\circ}$ байх адил хажуут $ABC$ гурвалжин өгөгдөв. $BC$ талын дундаж $M$ бол $\overrightarrow{AB}\cdot \overrightarrow{AM}$, $\overrightarrow{AB}\cdot \overrightarrow{BC}$, $\overrightarrow{AM}\cdot \overrightarrow{BC}$-г тус тус ол.
- $A(-1, 3)$, $B(1,-2)$, $C(-4,-1)$ цэгүүд өгөгдөв. $\overrightarrow{AB}\cdot \overrightarrow{CB}$-г ол.
- Дараах адилтгалыг батал. $$|\vec{\mathstrut{a}}+\vec{\mathstrut{b}}|^2+|\vec{\mathstrut{a}}-\vec{\mathstrut{b}}|^2=2\cdot \big(|\vec{\mathstrut{a}}|^2+|\vec{\mathstrut{b}}|^2\big).$$
- $|\vec{\mathstrut{a}}+\vec{\mathstrut{b}}|=4$, $|\vec{\mathstrut{a}}-\vec{\mathstrut{b}}|=2$ бол $\vec{\mathstrut{a}}\cdot \vec{\mathstrut{b}}$-г ол.
- Дараах нөхцлийг хангах $\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$; $\vec{\mathstrut{c}}$, $\vec{\mathstrut{d}}$-векторуудын хоорондох өнцгийг ол. (1) $|\vec{\mathstrut{a}}|=2$, $|\vec{\mathstrut{b}}|=3$, $\vec{\mathstrut{a}}\cdot \vec{\mathstrut{b}}=-3$ (2) $\vec{\mathstrut{c}}=(\sqrt{3}, 2)$, $\vec{\mathstrut{d}}=(2\sqrt{3},-3).$
- $|\vec{\mathstrut{a}}|=1$, $|\vec{\mathstrut{b}}|=2$, $|2\vec{\mathstrut{a}}-\vec{\mathstrut{b}}|=\sqrt{6}-\sqrt{2}$ үед $\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$ хоёр векторын хоорондох өнцөг $\theta, 0^{\circ}\leq\theta\leq 180^{\circ}$-г ол.
$\vec{\mathstrut{a}}=(x, 5)$, $\vec{\mathstrut{b}}=(1,-3)$
векторуудын хувьд
- $\vec{\mathstrut{a}}\perp \vec{\mathstrut{b}}$ бол $x$-г ол.
- $(2\vec{\mathstrut{a}}+3\vec{\mathstrut{b}})\parallel(\vec{\mathstrut{a}}+\vec{\mathstrut{b}})$ бол $x$-ыг ол.
$|\vec{\mathstrut{a}}|=1$
ба $|\vec{\mathstrut{a}}+t\vec{\mathstrut{b}}|$ нь $t=2$ үед
$\dfrac1{\sqrt{3}}$ гэсэн хамгийн бага утгандаа хүрдэг бол
$|\vec{\mathstrut{b}}|=\ebox$, $\vec{\mathstrut{a}}\cdot
\vec{\mathstrut{b}}=\ebox$ байна. Мөн энэ үед
$(\vec{\mathstrut{a}}+t\vec{\mathstrut{b}})$ ба
$\vec{\mathstrut{b}}$-ийн хоорондох өнцөг $\ebox^\circ$ байна.
- Координатын хавтгай дээр $\vec{\mathstrut{a}}=(4,-3)$, $\vec{\mathstrut{b}}=(2, 1)$ векторууд өгөгдөв. Хэрэв $\vec{\mathstrut{a}}+t\vec{\mathstrut{b}}$ ба $\vec{\mathstrut{b}}$ векторуудын хоорондох өнцөг $45^{\circ}$ бол $t$-ийн утгыг ол.
- Хавтгайд $0$, $A$, $B$, $C$ дөрвөн цэг өгөгдөв. Хэрэв $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}$, $OA=2$, $OB=1$, $OC=\sqrt{2}$ үед $\triangle OAB$-ийн талбайг ол.
Нэгж талтай $ABCDEF$ зөв зургаан
өнцөгтийн $BC$ талын дундаж цэг $G$ ба
$\overrightarrow{AB}=\vec{\mathstrut{a}}$, $\overrightarrow{AF}=\vec{\mathstrut{b}}$
байв. Хэрэв $H$ цэг нь $DE$ тал дээр орших ба $\overrightarrow{AH}\perp
\overrightarrow{FG}$ бол $\overrightarrow{AH}$-г $\vec{\mathstrut{a}}$,
$\vec{\mathstrut{b}}$-ээр илэрхийл.
Хавтгайн
$\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$ векторын хувьд
$|\vec{\mathstrut{a}}+3\vec{\mathstrut{b}}|=1$,
$|3\vec{\mathstrut{a}}-\vec{\mathstrut{b}}|=1$-ыг хангах үед
$|\vec{\mathstrut{a}}+\vec{\mathstrut{b}}|$-ын хамгийн их утга $M$
ба хамгийн бага утга $m$-ийг тус тус ол.
Хавтгайд $ABCD$
параллельограмм ба $PQR$ гурвалжин өгөгдөв.
$\overrightarrow{AP}=2\overrightarrow{AB}+3\overrightarrow{AC}$, $\overrightarrow{AQ}=3\overrightarrow{AB}+\overrightarrow{AC}$,
$\overrightarrow{AR}=\overrightarrow{AB}+2{AC}$ нөхцлүүд биелэх бол дараах нөхцлүүд
биелэхийг харуул.
(1) $QR\parallel BD, $ (2) $AB=AC$ байхад $PR\perp BC.$
Гурвалжны гурван орой $P$, $Q$, $R$-ийн
радиус векторууд, $\vec{\mathstrut{p}}$, $\vec{q}$, $\vec{r}$ байг. $PQ$ талыг
$3:2$ харьцаанд хуваах $A$, $QR$ талын үргэлжлэлийг $3:4$ харьцаанд хуваах $B$, $RP$
талын үргэлжлэлийг $4:1$ харьцаанд хуваах $C$
цэгүүд өгөгдөв. $ABC$ гурвалжны хүндийн төв $G$ бол дараах
векторуудыг $\vec{\mathstrut{p}}$, $\vec{q}$, $\vec{\mathstrut{r}}$-ээр илэрхийл.
- $A, B, C$ цэгүүдийн радиус векторууд;
- $\overrightarrow{AB}$;
- $G$-ийн радиус вектор.
- $\triangle ABC$ гурвалжны дотор $P$ цэг авав. $AP$ шулуун $BC$ хэрчмийг $Q$ цэгээр огтлох ба $BQ:QC=3:2$, $AP:PQ=2:1$ бол $5\overrightarrow{AP}+4\overrightarrow{BP}+6\overrightarrow{CP}=\overrightarrow{0}$ болохыг батал.
- $\triangle ABC$ ба $R$ цэгийн хувьд $6\overrightarrow{RA}+3\overrightarrow{RB}+2\overrightarrow{RC}=\overrightarrow{0}$ нөхцөл биелэх үед $R$ цэгийн байршлыг тодорхойл.
- Хавтгайд үл давхцах $A$, $B$, $C$, $D$ дөрвөн цэг өгөгдөв. $AB$, $CD$ хэрчмийг харгалзан $1:2$ харьцаанд хуваах $M$, $N$ цэгүүдийн хувьд $$2|\overrightarrow{AC}|+|\overrightarrow{BD}|\geq 3|\overrightarrow{MN}|$$ тэнцэл биш биелэхийг батал.
- Тэгш өнцөгт биш $ABC$ гурвалжныг багтаасан тойргийн төв $O$ байв. $H$ цэгийн хувьд $\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$ тэнцэл биелдэг бол $\overrightarrow{AH}\perp \overrightarrow{BC}$ болохыг батал.
- $ABC$ гурвалжны периметр $36$ нэгж ба түүнд багтсан тойргийн радиус 3 нэгж байв. Тэгвэл $Q$ цэг нь $6\overrightarrow{AQ}+3\overrightarrow{BQ}+2\overrightarrow{CQ}=\overrightarrow{0}$ нөхцлийг хангадаг бол $QBC$ гурвалжны талбайг ол.
- Хавтгайд $ABC$ гурвалжны дотор $P$ цэг өгөгдөв. $ABP$, $BPC$, $CPA$ гурвалжнуудын хүндийн төвүүд харгалзан $D$, $E$, $F$ бол $ABC$, $DEF$ гурвалжнуудын талбайн харьцааг ол.
- $\overrightarrow{OA}=\vec{a}$, $\overrightarrow{OB}=\vec{\mathstrut{b}}$, $|\vec{a}|=|\vec{\mathstrut{b}}|=1$, $\vec{a}\cdot \vec{\mathstrut{b}}=k$ үед $OA$ хэрчмийн дунджийг дайрсан түүнд перпендикуляр шулууны тэгшитгэлийг $t$-параметр болон $\vec{a}$, $\vec{\mathstrut{b}}$, $k$-аар илэрхийл.
- Нэгж талтай $ABCDEF$ зөв зургаан өнцөгтийн хувьд $\overrightarrow{AB}=\vec{a}$, $\overrightarrow{AF}=\vec{\mathstrut{b}}$ бол түүнд багтсан тойргийн тэгшитгэлийг $\vec{a}$, $\vec{\mathstrut{b}}$-аар илэрхийл.
- $A(-2, 3)$ цэгийг дайрах ба $5x+4y-20=0$ шулуунд перпендикуляр шулууны тэгшитгэлийг бич.
$ABC$ гурвалжин өгөгдөв. Дараах
нөхцлийг хангах $P$ цэгийн геометр байрыг ол.
- $\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}$, $s+2t=3$, $s\geq 0$, $t\geq 0.$
- $\overrightarrow{OP}=r\overrightarrow{OA}+s\overrightarrow{OB}+t\overrightarrow{OC}$, $r+s+t=1$, $r\geq 0, s\geq 0, t\geq 0.$
- $C(\vec{\mathstrut{c}})$ дээр төвтэй, $r$ радиустай тойрог дээр байрлах $P_0(\vec{\mathstrut{p}}_0)$ цэгт татсан шүргэгч шулууны тэгшитгэл нь $(\vec{\mathstrut{p}}_0-\vec{\mathstrut{c}})(\vec{\mathstrut{p}}-\vec{\mathstrut{c}})=r^2$ болохыг харуул.
- $2x+y-6=0$, $x+3y-5=0$ хоёр шулууны хоорондох өнцгийг ол.
- $OAB$ гурвалжны хувьд $\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$, $3x+2y\leq 6$, $x\geq 0$, $y\geq 0$ нөхцлүүдийг хангах $P$ цэгийн геометр байрыг ол.
$OAB$ гурвалжны хувьд $|\overrightarrow{OA}|=3$,
$|\overrightarrow{OB}|=2$, $\overrightarrow{OA}\cdot \overrightarrow{OB}$=4 байв. $OA$ талыг $A$ цэг
шүргэх тойргийн төв $C$ нь $O$ оройн өнцгийн биссектрис дээр
оршино. Тэгвэл $\overrightarrow{OC}=\vec{\mathstrut{c}}$ векторыг $\overrightarrow{OA}=\vec{a}$,
$\overrightarrow{OB}=\vec{\mathstrut{b}}$ векторуудаар илэрхийл.
$ABC$ гурвалжин өгөгдөв. $P$ цэгийн хувьд $\overrightarrow{PA}+2\overrightarrow{PB}+3\overrightarrow{PC}=k\cdot
\overrightarrow{AB}, (k\in
\mathbb R)$ нөхцлийг хангах бол
- $P$ цэгийн геометр байрыг ол;
- $P$ цэг $ABC$ гурвалжин дотор орших $k$-ийн утгын мужийг ол.
$AD\parallel BC$ ба $AD:BC=1:2$ байх $ABCD$ дөрвөн өнцөгт өгөгдөв.
$AB$ талыг $1:3$ харьцаанд хуваах $E$, $CD$ талыг $4:3$ харьцаанд
хуваах $F$ цэгүүд авъя. Мөн $AC$, $BD$ диагоналиудын огтлолцлыг
$P$ гэвэл $P$ цэг нь $EF$ хэрчим дээр оршихыг батал.
$OAB$ гурвалжны $OA$, $OB$
талуудыг харгалзан $3:1$, $4:1$ харьцаанд хуваах $D$, $C$
цэгүүдийг авав. $AC$, $BD$-ийн огтлолцлын цэгийг $P$ гэе.
$\overrightarrow{OA}=\vec{\mathstrut{a}}$, $\overrightarrow{OB}=\vec{\mathstrut{b}}$ бол $\overrightarrow{OP}$ векторыг
$\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$ векторуудаар илэрхийл.
$ABCD$ параллелограммын $AB$,
$BC$ талуудыг харгалзан $3:2$, $1:2$ харьцаанд хуваах $E$, $F$
цэгүүд өгөгдөв. Мөн $CD$ талын дундаж $M$ байв. $CE$, $FM$ хэрчмүүд $P$ цэгт огтлолцох ба $\overrightarrow{AB}=\vec{\mathstrut{a}}$, $\overrightarrow{AD}=\vec{\mathstrut{b}}$ бол $\overrightarrow{AP}$ векторыг $\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$-ээр илэрхийл.
- Дөрвөн өнцөгтийн эсрэг талуудын дунджийг холбосон хэрчмүүд, диагоналиудын дунджийг холбосон хэрчимтэй нэг цэгт огтлолцохыг батал.
- $ABC$ гурвалжны $BC$, $CA$, $AB$ талууд дээр харгалзан $D$, $E$, $F$ цэгүүдийг авъя. $ABC$ болон $DEF$ гурвалжнуудын хүндийн төвүүд давхцах үед $BD:DC=CE:EA=AF:FB$ биелэхийг батал.
- $ABC$ гурвалжны $A$ оройн өнцөг $\theta$ ба $\overrightarrow{AB}=(a,b)$, $\overrightarrow{AC}=(c,d)$ байг. Тэгвэл $ABC$ гурвалжны талбайг $S$ гэвэл $S=\dfrac12|ad-bc|$ болохыг батал.
- $A(4, 2\sqrt{5})$, $B(\sqrt{3}, 1)$, $C(3\sqrt{5}, 3)$ байх $ABC$ гурвалжны талбайг ол.
$ABC$ гурвалжны хувьд
$AB=3$, $AC=2$ ба $BC$, $CA$ талуудыг харгалзан $1:2$, $4:1$
харьцаанд хуваах $D$, $E$ цэгүүд өгөгдөв. $AD$, $BE$ шулуунуудын
огтлолцлын цэг $M$, $CM$ шулуун $AB$ талын огтлолцлын цэг $F$ ба
$CF$ шулуун $AB$ талд перпендикуляр бол
- $\overrightarrow{CF}$ векторыг $\overrightarrow{AB}$, $\overrightarrow{AC}$-ээр илэрхийл.
- $ABC$ гурвалжны талбай $S$-ыг ол.
- $A$ оройгоос татсан өндөр $CF$ шулуунтай $G$ цэгт огтлолцох үед $AG$ хэрчмийн уртыг ол.
$BC$ гипотенуз бүхий $ABC$ адил хажуут тэгш өнцөгт гурвалжны гадна
талд $AB$, $AC$ катетуудаар харгалзан талаа хийсэн $ABK$, $ACL$
зөв гурвалжнууд байгуулав. $BL$, $CK$ нь $M$ цэгт огтлолцдог ба
$\overrightarrow{AB}=\vec{\mathstrut{b}}$, $\overrightarrow{AC}=\vec{\mathstrut{c}}$ бол
- $\overrightarrow{AK}$, $\overrightarrow{AL}, $
- $\overrightarrow{BL}$, $\overrightarrow{CK}$ векторуудыг тус тус $\vec{\mathstrut{b}}$, $\vec{\mathstrut{c}}$-ээр илэрхийл.
- $KML$ өнцгийг ол.
$ABC$ гурвалжны хувьд $\overrightarrow{AB}=\vec{\mathstrut{b}}$,
$\overrightarrow{AC}=\vec{\mathstrut{c}}$, $\vec{\mathstrut{b}}\cdot\vec{\mathstrut{c}}=m$, $|\vec{\mathstrut{b}}|=b$,
$|\vec{\mathstrut{c}}|=c$ байв. $C$, $D$ цэгүүд $AB$ шулууны хувьд тэгш
хэмтэй, $B$, $E$ цэгүүд $AC$ шулууны хувьд тэгш хэмтэй байв.
- $\overrightarrow{AD}$, $\overrightarrow{DE}$-г $\vec{\mathstrut{b}}$, $\vec{\mathstrut{c}}$, $m$, $b$, $c$-ээр илэрхийл.
- $\overrightarrow{DE}\parallel \overrightarrow{BC}$ үед $ABC$ гурвалжин ямар өнцөгт гурвалжин байх вэ?
Хурц өнцөгт $ABC$ гурвалжныг багтаасан тойргийн төв $O$, өндрүүдийн огтлолцлын цэг
$H$ байг.
- $\overrightarrow{OA}=\vec{\mathstrut{a}}$, $\overrightarrow{OB}=\vec{\mathstrut{b}}$, $\overrightarrow{OC}=\vec{\mathstrut{c}}$ бол $\overrightarrow{OH}$-г $\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$, $\vec{\mathstrut{c}}$-ээр илэрхийл.
- Тойрог дээрх $P$ цэгийн хувьд $\overrightarrow{OQ}=\dfrac 12(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})-\dfrac 12\overrightarrow{OP}$ нөхцлийг хангах цэгийг $Q$ гэе. $P$ цэг $O$-ийн хувьд $A$-тай тэгш хэмтэй үед $Q$-ийн байршлыг тодорхойл. Мөн $P$ цэг нь тойрог дээгүүр хөдлөх үед $Q$-ийн геометр байрыг тодорхойл.
$OAB$ гурвалжны $AB$ тал дээрх $P$
$(P\ne A, P\ne B)$ цэгээс $OA$, $OB$ шулуунд харгалзан $PQ$, $PR$
перпендикуляруудыг татав. $OP$ ба $QR$ шулуунууд перпендикуляр ба
$\overrightarrow{OA}=\vec{\mathstrut{a}}$, $\overrightarrow{OB}=\vec{\mathstrut{b}}$, $\overrightarrow{OP}=\vec{\mathstrut{p}}$ байв.
- $\overrightarrow{OQ}$-г $s\vec{\mathstrut{a}}$,, $\overrightarrow{QR}$-г $u\vec{\mathstrut{a}}+v\vec{\mathstrut{b}}$ хэлбэртэй илэрхийл.
- $\vec{\mathstrut{p}}\cdot\vec{\mathstrut{a}}>0$ болохыг харуул.
- $\vec{\mathstrut{p}}=(1-t)\vec{\mathstrut{a}}+t\vec{\mathstrut{b}}$ гэвэл $t$-г $|\vec{\mathstrut{a}}|$, $|\vec{\mathstrut{b}}|$-ээр илэрхийл.
$OXY$ хавтгайд $S(s,s)$, $T(-t,t)$ цэг авав. Энд $s\geq 0$, $t\geq 0$ ба $s^2+t^2=2$ байв. Мөн $P(x,y)$ $(|x|\leq y)$ цэгийг $SPT$ нь зөв гурвалжин байхаар авчээ. $ST$ хэрчмийн дундаж $M$ бөгөөд $PM$ шулуун $OX$ тэнхлэгийг $R$ цэгт огтолно. Тэгвэл $ST=2$, $OM=1$, $MR=1$ болохыг тус тус харуул. Мөн $\overrightarrow{OM}$ нь $OX$ тэнхлэгийн эерэг чиглэлтэй $\theta$ өнцөг үүсгэдэг бол $P$ цэгийн координатыг $\theta$-өөр илэрхийл.
$x, y, u, v$ нь $x^2+y^2=1$,
$(u-2)^2+(v-2\sqrt{3})=1$ нөхцлийг хангах үед $ux+vy$-ийн хамгийн
их, хамгийн бага утгыг тус тус ол.
$\vec{\mathstrut a}=(1;-2)$, $\vec{\mathstrut b}=(-2;2)$ бол $\vec{\mathstrut a}\cdot(\vec{\mathstrut a}-2\vec{\mathstrut b})$-г ол.
A. $18$
B. $13$
C. $14$
D. $16$
E. $17$
$\vec{\mathstrut a}=(2;3)$, $\vec{\mathstrut b}=(-1;1)$ бол $\vec{\mathstrut a}\cdot(\vec{\mathstrut a}-3\vec{\mathstrut b})$-г ол.
A. $13$
B. $6$
C. $-10$
D. $10$
E. $11$
$\vec{\mathstrut a}=(5; y; -6)$, $\vec{\mathstrut b}=(x; 2; 2)$ векторууд коллинеар байх $x, y$-ийн үржвэр аль нь вэ?
A. $-8$
B. $8$
C. $10$
D. $12$
E. $6$
$\vec{\mathstrut a}+\vec{\mathstrut b}=(1,3,2)$, $2\vec{\mathstrut a}+\vec{\mathstrut b}=(3,4,1)$ байх $\vec{\mathstrut a}$, $\vec{\mathstrut b}$ векторын хоорондох өнцгийн косинусыг ол.
A. $\dfrac{2\sqrt{21}}3$
B. $-\dfrac{\sqrt{21}}{14}$
C. $-\dfrac{2\sqrt{17}}{17}$
D. $-\dfrac7{3\sqrt{15}}$
E. $\dfrac{\sqrt{55}}{11}$
Хоорондоо параллел байх векторууд аль нь вэ?
A. $\vec{\mathstrut a}=(2,1,0)$ ба $\vec{\mathstrut b}=(0,1,2)$
B. $\vec{\mathstrut a}=(-1,2,1)$ ба $\vec{\mathstrut b}=(-2,1,2)$
C. $\vec{\mathstrut a}=(1,-1,1)$ ба $\vec{\mathstrut b}=(1,-2,1)$
D. $\vec{\mathstrut a}=(2,-1,1)$ ба $\vec{\mathstrut b}=(4,-2,2)$
E. $\vec{\mathstrut a}=(0,0,1)$ ба $\vec{\mathstrut b}=(1,0,0)$
$(1;a;b)$, $(x;x;x)$, $x\not=0$ векторууд параллель бол $a+b=?$
A. 1
B. 2
C. 3
D. 4
E. 5
Дараах векторуудын аль нь нэгж вектор вэ?
A. $(1;1)$
B. $(1/2;1/2)$
C. $(\sin 36^\circ;-\sin 54^\circ)$
D. $(\log_23;1-\log_23)$
E. аль нь ч биш
$|\vec{u}|=5$, $|\vec{v}|=2$ ба $\vec{u},\vec{v}$ векторуудын хоорондох өнцөг $120^\circ$ бол $|\vec{u}-2\vec{v}|^2$ хэдтэй тэнцүү вэ?
A. $14$
B. $61$
C. $41$
D. $82$
E. $21$
$|\vec{u}|=3$, $|\vec{v}|=2$, $\vec{u}\cdot\vec{v}=3$ бол $|2\vec{u}-3\vec{v}|$-ийг ол.
A. 3
B. 4
C. 5
D. 6
E. 7
$\vec{\mathstrut a}=(1;2;3)$, $\vec{\mathstrut b}=(x;2;1)$ ба $\vec{\mathstrut a}\perp \vec{\mathstrut b}$ бол $x=?$
A. $-7$
B. $7$
C. $3$
D. $-3$
E. $0$
$\vec{\mathstrut a}\not\parallel\vec{\mathstrut b}$ векторууд өгөгдөв. Дараах векторуудын аль нь параллел вэ?
A. $\vec{\mathstrut a}+2\vec{\mathstrut b}$ ба $-2\vec{\mathstrut a}-4\vec{\mathstrut b}$
B. $\vec{\mathstrut a}+\vec{\mathstrut b}$ ба $\vec{\mathstrut a}-\vec{\mathstrut b}$
C. $\vec{\mathstrut a}$ ба $-2\vec{\mathstrut b}$
D. $\vec{\mathstrut b}$ ба $2\vec{\mathstrut a}$
E. Эдгээрийн аль нь ч параллел байж чадахгүй
$\vec{u}=(1,2)$, $\vec{v}=(-2,1)$ бол $\vec{u}\cdot(\vec{v}+2\vec{u})=?$
A. $0$
B. $5$
C. $6$
D. $8$
E. $10$
$A(3,5)$, $B(7,10)$ байв. $\dfrac{\overrightarrow{AC}}{\overrightarrow{CB}}=4$ байх $C$ цэгийг ол.
A. $\left(\dfrac{13}{5};5\right)$
B. $\left(\dfrac{1}{5},\frac{\sqrt{29}}{5}\right)$
C. $(3;2)$
D. $\left(5;\dfrac{13}{5}\right)$
E. $\left(\dfrac{31}{5};9\right)$
$\vec{u}=(1;3)$, $\vec{v}=(x;y)$ байв. Хэрвээ $\vec{u}\parallel\vec{v}$ бол
A. $x+y=0$
B. $x+3y=0$
C. $3x+y=0$
D. $x-y=0$
E. $3x-y=0$
$2x-3y+z-5=0$, $ax+3y-z+5=0$ тэгшитгэлтэй хоёр хавтгай
$a$-ийн ямар утганд харилцан перпендикуляр байх вэ?
A. $4$
B. $5$
C. $3$
D. $7$
E. $8$
$M(4,-2,1)$ цэгээс $\vec a=(1,5,-1)$ вектор татахад аль цэгт төгсөх вэ?
A. $(3,-7,2)$
B. $(5,3,0)$
C. $(-3,7,-2)$
D. $(5,3,2)$
E. $(-3,-7,-2)$
$M(-1;1;2)$ цэгээс $\vec a=(1;-1;-2)$ вектор татахад дараах
4 цэгийн аль нь гарах вэ?
A. $(2;-2;-4)$
B. $(-2;2;4)$
C. $(0;0;0)$
D. $(2;2;0)$
E. $(-2;-2;-4)$
$ABC$ гурвалжны $AC$ суурьтай параллель дундаж шугам $MN$
байв. $\overrightarrow{MN}=x\,\overrightarrow{CA}$ байх $x$-ийн утга аль вэ?
A. $2$
B. $\dfrac12$
C. $3$
D. $\dfrac13$
E. $-2$
$ABC$ гурвалжны $AB$ талын дундаж $M$, $BC$ талын дундаж $N$
байхад $\overrightarrow{MN}=x\,\overrightarrow{AC}$ бол $x$-ийн утга аль вэ?
A. $\frac12$
B. $-2$
C. $-\frac12$
D. $2$
$ABC$ гурвалжны $AA_1$, $BB_1$ медианы огтлолын цэг $O$ бол
$\overrightarrow{OA}=\lambda\overrightarrow{AA_1}$ байх $\lambda$-ийн утга аль вэ?
A. $\dfrac13$
B. $\dfrac23$
C. $-\dfrac23$
D. $-\dfrac13$
E. $\dfrac43$
$ABC$ гурвалжны $AA_1$, $BB_1$ медианы огтлолын цэг $O$ бол
$\overrightarrow{OB_1}=\lambda\,\overrightarrow{BB_1}$ байх $\lambda$-ийн утга аль вэ?
A. $\dfrac23$
B. $\dfrac13$
C. $-\dfrac13$
D. $-\dfrac23$
E. $\dfrac43$
$\vec{\mathstrut a}=(4;2;5)$, $\vec{\mathstrut b}=(-5;0;4)$ бол $\vec{\mathstrut a}, \vec{\mathstrut b}$ векторын хоорондох өнцгийн хэмжээ аль вэ?
A. $60^\circ$
B. $30^\circ$
C. $45^\circ$
D. $90^\circ$
E. $10^\circ$
$\vec a=(1;1;0)$, $\vec b=(0;1;-1)$ бол хоёр векторын
хоорондох өнцгийн хэмжээ хэдэн радиан бэ?
A. $\dfrac{\pi}2$
B. $\dfrac{\pi}6$
C. $\dfrac{\pi}3$
D. $\dfrac{\pi}4$
E. $\dfrac{\pi}{5}$
$\vec{\mathstrut a}+\vec{\mathstrut b}=(1;3;2)$, $2\vec{\mathstrut a}+\vec{\mathstrut b}=(3;4;1)$ бол $\vec{\mathstrut a}$, $\vec{\mathstrut b}$ хоёр векторын скаляр үржвэр хэд гарах вэ?
A. $3$
B. $-2$
C. $-3$
D. $2$
E. $0$
$\vec{\mathstrut a}=(1;1;0)$, $\vec{\mathstrut b}=(0;\lambda;1)$. $\vec{\mathstrut a}, \vec{\mathstrut b}$-ийн хоорондох өнцгийн хэмжээ $60^\circ$ бол $\lambda$-ийн утга
аль байх вэ?
A. $2$
B. $3$
C. $1$
D. $-2$
E. $-1$
$\vec a=(0;1;1)$, $\vec b=(1;0;\lambda)$. $\vec a, \vec
b$-ийн хоорондох өнцгийн хэмжээ $120^\circ$ бол $\lambda$-ийн утга
аль вэ?
A. $1$
B. $-1$
C. $2$
D. $-2$
E. $-\dfrac12$
$2x-3y-4z+5=0$ хавтгайтай $\vec a=(\lambda;-1;2)$ вектор
параллель бол $\lambda$-ийн утга аль вэ?
A. $2$
B. $1.5$
C. $2.5$
D. $3$
E. $4$
$2x+\lambda y+3z-3=0$ хавтгай $\lambda$-ийн аль утганд $\vec a=(-1;2;-4)$ вектортэй параллел байх вэ?
A. $5$
B. $4$
C. $6$
D. $7$
E. $8$
$\vec{\mathstrut a}=(0.5;-1;1.5)$, $\vec{\mathstrut b}=(-1;2;-3)$ векторууд дараах
аль нөхцөлийг хангах вэ?
A. $\vec{\mathstrut a}\perp \vec{\mathstrut b}$
B. $\vec{\mathstrut a}\uparrow\uparrow\vec{\mathstrut b}$
C. $\vec{\mathstrut a}\uparrow\downarrow\vec{\mathstrut b}$
D. $\vec{\mathstrut a}=\vec{\mathstrut b}$
E. Эдгээрийн аль нь ч биш
$\vec a=(2;-1;0)$, $\vec b=(1;2;3)$ векторууд дараах аль
нөхцөлийг хангах вэ?
A. $\vec a=\vec b$
B. $\vec a\perp\vec b$
C. $\vec a\uparrow\uparrow\vec b$
D. $\vec a\uparrow\downarrow\vec b$
E. $\vec a=-\vec b$
$2\vec{\mathstrut a}+\vec{\mathstrut b}=(-3;2;4)$, $\vec{\mathstrut a}+\vec{\mathstrut b}=(-1;3;2)$ байх $\vec{\mathstrut a}$, $\vec{\mathstrut b}$ векторын хоорондох өнцгийн косинусыг ол.
A. $\dfrac{2\sqrt{21}}{3}$
B. $-\dfrac{\sqrt{21}}{14}$
C. $-\dfrac{2\sqrt{17}}{17}$
D. $-\dfrac{7}{3\sqrt{15}}$
E. $\dfrac{\sqrt{55}}{11}$
Хоорондоо параллел байх векторууд аль нь вэ?
A. $\vec{\mathstrut a}=(2,1,0)$ ба $\vec{\mathstrut b}=(0,1,2)$
B. $\vec{\mathstrut a}=(-1,2,1)$ ба $\vec{\mathstrut b}=(-2,1,2)$
C. $\vec{\mathstrut a}=(1,-1,1)$ ба $\vec{\mathstrut b}=(1,-2,1)$
D. $\vec{\mathstrut a}=(2,-1,1)$ ба $\vec{\mathstrut b}=(1,-1,2)$
E. $\vec{\mathstrut a}=(1,0,-2)$ ба $\vec{\mathstrut b}=(3,0,-6)$
$\vec{p}$, $\vec{q}$ векторууд $|\vec{p}+3\vec{q}|=1$, $|3\vec{p}-\vec{q}|=1$ нөхцөлийг хангах үед $|\vec{p}+\vec{q}|$-ийн хамгийн их ба бага утгыг харгалзан $M$, $m$ гэе. $M-m=?$
A. $\dfrac{1}{5}$
B. $\dfrac{1}{3}$
C. $\dfrac{2}{3}$
D. $\dfrac{2}{5}$
E. $\dfrac{3}{4}$
$\vec{m}=(-4,2,2)$, $\vec{n}=(2,-2,0)$ векторуудын хоорондох өнцгийг ол.
A. $30^\circ$
B. $45^\circ$
C. $60^\circ$
D. $120^\circ$
E. $150^\circ$
$A(3;4)$, $B(-1;1)$ бол $\overrightarrow{AB}$ векторын координатыг заа.
A. $(4;-3)$
B. $(4;3)$
C. $(2;5)$
D. $(-4;-3)$
E. $(-4;3)$
$\vec{m}=(-2,1,2)$, $\vec{n}=(1,-1,0)$ векторуудын хоорондох өнцгийг ол.
A. $30^\circ$
B. $45^\circ$
C. $60^\circ$
D. $120^\circ$
E. $135^\circ$
$\vec{m}=(1;-4;x)$, $\vec{n}=(y;-2;5)$ векторууд параллель бол $x+y=?$
A. $5$
B. $10$
C. $10\dfrac12$
D. $12\dfrac13$
E. $13\dfrac12$
$\vec{p}=(y+1,3)$, $\vec{q}=(2,y-1)$ ба $\vec{p}\perp\vec{q}$ бол $y=?$
A. $-0.1$
B. $0$
C. $0.1$
D. $0.2$
E. $-0.2$
$\vec{\mathstrut a}=(6,2)$, $\vec{\mathstrut b}=(1,x)$ векторууд перпендикуляр бол $x$-г ол.
A. $\frac13$
B. $-3$
C. $2$
D. $-2$
E. $-6$
$\vec{\mathstrut a}\big(\frac12;-3\big)$, $\vec{\mathstrut b}(-1;2)$ векторууд аль нөхцлийг хангах вэ?
A. $\vec{\mathstrut a}\uparrow\uparrow\vec{\mathstrut b}$
B. $\vec{\mathstrut a}\perp\vec{\mathstrut b}$
C. $\vec{\mathstrut a}\uparrow\downarrow\vec{\mathstrut b}$
D. $\vec{\mathstrut a}=\vec{\mathstrut b}$
E. эдгээрийн аль нь ч биш
$\vec{\mathstrut a}=(5,3), \vec{\mathstrut b}=(x,-10)$ векторууд перпендикуляр бол $x$-г ол.
A. $\frac13$
B. $6$
C. $2$
D. $-2$
E. $-6$
$\vec{\mathstrut a}$; $\vec{\mathstrut b}$ векторын уртууд нь харгалзан $\sqrt{26}$; $\sqrt{13}$ бөгөөд хоорондох өнцөг нь $\arcsin\dfrac5{13}$ бол тэдгээрийн скаляр үржвэрийг ол.
A. $14\sqrt2$
B. $12\sqrt3$
C. $12\sqrt6$
D. $12\sqrt2$
E. $12$
$\vec{\mathstrut a}$; $\vec{\mathstrut b}$ векторын уртууд нь харгалзан $\sqrt{17}$; $\sqrt{34}$ бөгөөд хоорондох өнцөг нь $\arcsin\dfrac{15}{17}$ бол тэдгээрийн скаляр үржвэрийг ол.
A. $8\sqrt5$
B. $8\sqrt2$
C. $7\sqrt2$
D. $15\sqrt2$
E. $17$
$\vec{\mathstrut a}$; $\vec{\mathstrut b}$ векторын уртууд нь харгалзан $\sqrt{10}$; $\sqrt{5}$ бөгөөд хоорондох өнцөг нь $\arcsin\dfrac35$ бол тэдгээрийн скаляр үржвэрийг ол.
A. $4\sqrt2$
B. $2\sqrt2$
C. $\sqrt2$
D. $3\sqrt2$
E. $1$
$\vec{\mathstrut a}$; $\vec{\mathstrut b}$ векторын уртууд нь харгалзан $\sqrt{15}$; $\sqrt{10}$ бөгөөд хоорондох өнцөг нь $\arcsin\dfrac45$ бол тэдгээрийн скаляр үржвэрийг ол.
A. $4\sqrt6$
B. $3\sqrt6$
C. $\sqrt6$
D. $3\sqrt5$
E. $2\sqrt6$
$\vec{\mathstrut a}$; $\vec{\mathstrut b}$ векторын уртууд нь харгалзан $\sqrt{10}$; $\sqrt{5}$ бөгөөд хоорондох өнцөг нь $\arcsin\dfrac35$ бол тэдгээрийн скаляр үржвэрийг ол.
A. $4\sqrt2$
B. $2\sqrt2$
C. $\sqrt2$
D. $3\sqrt2$
E. $1$
Хоорондоо параллель байх векторууд аль нь вэ?
A. $\vec{\mathstrut a}=(1;2;0)$ ба $\vec{\mathstrut b}=(0;1;2)$
B. $\vec{\mathstrut a}=(-1;1;1)$ ба $\vec{\mathstrut b}=(1;1;1)$
C. $\vec{\mathstrut a}=(1;-1;1)$ ба $\vec{\mathstrut b}=(1;-2;1)$
D. $\vec{\mathstrut a}=(2;-1;1)$ ба $\vec{\mathstrut b}=(1;-1;2)$
E. $\vec{\mathstrut a}=(1;0;-2)$ ба $\vec{\mathstrut b}=(3;0;-6)$
Хоорондоо параллель байх векторууд аль нь вэ?
A. $\vec{\mathstrut a}=(-2;1;1)$ ба $\vec{\mathstrut b}=(2;1;1)$
B. $\vec{\mathstrut a}=(1;3;0)$ ба $\vec{\mathstrut b}=(0;1;3)$
C. $\vec{\mathstrut a}=(2;0;-1)$ ба $\vec{\mathstrut b}=(4;0;-2)$
D. $\vec{\mathstrut a}=(2;-1;0)$ ба $\vec{\mathstrut b}=(0;-1;2)$
E. $\vec{\mathstrut a}=(1;-1;1)$ ба $\vec{\mathstrut b}=(1;-2;1)$
$(a;2;b)$, $(x;x;x)$, $x\not=0$ векторууд параллель бол $a+b=?$
A. 1
B. 2
C. 3
D. 4
E. 5
$(1;a;b)$, $(x;2x;3x)$, $x\not=0$ векторууд параллель бол $a+b=?$
A. 1
B. 2
C. 3
D. 4
E. 5
$(1;a;b)$, $(x;3x;2x)$, $x\not=0$ векторууд параллель бол $a+b=?$
A. 1
B. 2
C. 3
D. 4
E. 5
$\vec{\mathstrut a}=(4;2;5)$, $\vec{\mathstrut b}=(-5;0;4)$ бол $\vec{\mathstrut a}, \vec{\mathstrut b}$ векторын хоорондох өнцгийн хэмжээ аль вэ?
A. $60^\circ$
B. $30^\circ$
C. $45^\circ$
D. $90^\circ$
E. $10^\circ$
$\vec{\mathstrut a}=(-1;1;0)$, $\vec{\mathstrut b}=(0;1;-1)$ бол хоёр векторын
хоорондох өнцгийн хэмжээ хэдэн радиан бэ?
A. $\dfrac{\pi}2$
B. $\dfrac{\pi}6$
C. $\dfrac{\pi}3$
D. $\dfrac{\pi}4$
E. $\dfrac{\pi}{5}$
$f(x)=2x+a$ функц дээр $M(-1, 3)$ цэг оршдог бол $a$ тоог ол
A. $(3 )$
B. $( 4)$
C. $(5)$
D. $(6)$
E. $(7)$
$ABCD$ параллелограммын $AB$, $BC$ талуудыг харгалзан $3:2$, $1:2$ харьцаанд хуваах $E$, $F$ цэгүүд өгөгдөв. Мөн $CD$ талын дундаж $M$ байв. $CE$, $FM$ хэрчмүүд $P$ цэгт огтлолцох ба $\overrightarrow{AB}=\vec{\mathstrut{a}}$, $\overrightarrow{AD}=\vec{\mathstrut{b}}$ бол $\overrightarrow{AP}$ векторыг $\vec{\mathstrut{a}}$, $\vec{\mathstrut{b}}$-ээр илэрхийл.
A. $\dfrac{11}{23}\vec{\mathstrut{a}}+\dfrac{12}{23}\vec{\mathstrut{b}}$
B. $\dfrac{10}{23}\vec{\mathstrut{a}}+\dfrac{13}{23}\vec{\mathstrut{b}}$
C. $\dfrac{19}{23}\vec{\mathstrut{a}}+\dfrac{13}{23}\vec{\mathstrut{b}}$
D. $\dfrac{13}{23}\vec{\mathstrut{a}}+\dfrac{19}{23}\vec{\mathstrut{b}}$
E. $\dfrac{12}{23}\vec{\mathstrut{a}}+\dfrac{11}{23}\vec{\mathstrut{b}}$
$\vec{\mathstrut a}=(1;-2)$, $\vec{\mathstrut b}=(-2;2)$ бол $|\vec{\mathstrut a}-2\vec{\mathstrut b}|$-г ол.
A. $7.5$
B. $7$
C. $\sqrt{51}$
D. $8$
E. $\sqrt{61}$
$\vec{\mathstrut a} = (-1,-2, 3)$ , $ \vec{\mathstrut b} = (1, -2, -3)$ бол $ \vec{\mathstrut a}- \vec{\mathstrut b} = ?$
A. $ (-2, 0 , 6) $
B. $ (0, -4, 0) $
C. $ (-2, 0, -6) $
D. $ (2, 0, -6) $
E. $ (2, -4, 2) $
$f(x)=2x+a$ функц дээр $M(-1, 3)$ цэг оршдог бол $a$ тоог ол
A. $(3 )$
B. $( 4)$
C. $(5)$
D. $(6)$
E. $(7)$
$ \vec{\mathstrut a}= (-2,-3, 4)$ , $ \vec{\mathstrut b} = (2, -3, -4)$ бол $\vec{\mathstrut a}- \vec{\mathstrut b} =?$
A. $ (-4, 0 , 8) $
B. $ (4, -4, 0) $
C. $ (-2, 6, -8) $
D. $ (4, 0, -6) $
E. $ (2, -4, 8) $
$ABCD-EFGH$ параллелепипедийн $AB$, $AD$ талуудыг $2:1$ харьцаагаар хуваах цэгүүд нь харгалзан $P$, $Q$ ба $EG$ хэрчмийг $1:2$ харьцаагаар хуваах цэг нь $R$ байв. Параллелепипедийн $AG$ диагональ $PQR$ гурвалжны хүндийн төв $K$-г дайрах бол $K$ цэг $AG$-г $\fbox{a}:\fbox{b}$ харьцаагаар хуваана. $\overrightarrow{AG}=\fbox{c}\overrightarrow{AK}$
$|\vec{a}-2\vec{b}|=1$, $|2\vec{a}-5\vec{b}|=1$ байх $\vec{a}$ ба $\vec{b}$ векторууд өгөгдөв.
- $\vec{a}-2\vec{b}=\vec{p}, 2\vec{a}-5\vec{b}=\vec{q}$ бол $\vec{a}=\fbox{a}\cdot\vec{p}-\fbox{b}\cdot\vec{q}$, $\vec{b}=\fbox{c}\cdot\vec{p}-\fbox{d}\cdot\vec{q}$.
- $|\vec{a}+\vec{b}|$-ийн хамгийн их утга нь $\fbox{ef}$.
- $|\vec{a}+\vec{b}|$-ийн хамгийн бага утга нь $\fbox{g}$.
$\vec{u}(7;-1)$ ба $\vec{v}(4;4)$ векторуудын хоорондох өнцөг
$\alpha$ гэвэл $1+\cos2\alpha=\dfrac{\fbox{cd}}{\fbox{ab}}$ байна.
$\vec p=(x^2-x-2)\vec m$, $\vec q=x\vec m$ векторууд эсрэг
чиглэлтэй байх $x$-ийн утгууд
$]-\infty;-\fbox{a}[\cup]\fbox{b};\fbox{c}[$ олонлог үүсгэх ба
тэдгээрээс $x=-\fbox{d}$, $x=\fbox{e}$ байхад $\vec p$ нь $\vec q$-ээс
2 дахин урт байна $\vec m\ne\vec 0$.
$\vec p=(3x^2-11x+6)\vec m$, $\vec q=(x^2+1)\vec m$
векторууд эсрэг чиглэлтэй байх $x$-ийн утгууд
$\Bigl]\frac{\fbox{a}}{\fbox{b}};\fbox{c}\Bigr[$ олонлог үүсгэх ба
тэдгээрээс $x=\dfrac{\fbox{d}}4$, $x=\fbox{e}$ байхад уг векторууд
ижил урттай байна $\vec m\ne\vec 0$.
$\vec p,\vec q,\vec r$ векторууд нэг хавтгайд байрлах ба хос
хосоороо хоорондоо $120^\circ$ өнцөг үүсгэнэ. Хэрэв $|\vec p|=1$,
$|\vec q|=2$, $|\vec r|=3$ бол $\vec r$ нь $\vec p$, $\vec q$
векторуудаар $\vec r=-\dfrac{\fbox{a}}{\fbox{b}}\vec p-\fbox{c}\vec q$
гэж задрана.
$\vec p,\vec q,\vec r$ векторууд нэг хавтгайд байрлах ба
$\vec r$ нь $\vec p$, $\vec q$ вектор тус бүртэй $60^\circ$ өнцөг
үүсгэнэ. Хэрэв $|\vec p|=3$, $|\vec q|=2$, $|\vec r|=1$ бол $\vec
p$ нь $\vec q$, $\vec r$ векторуудаар $\vec
p=\displaystyle-\frac{\fbox{a}}{\fbox{b}}\vec q+\fbox{c}\vec r$ гэж задрана.
$A(1;1)$, $B(6;6)$, $C(5;4)$, $D(2;1)$ цэгүүдэд оройтой
трапецийн дундаж шугамын урт $\fbox{a}\sqrt{\fbox{b}}$, $D$ оройн
гадаад өнцөг $\fbox{cd}^\circ$ байна.
$A(1;1)$, $B(2;1)$, $C(5;4)$ цэгүүдэд оройтой гурвалжны
мохоо өнцгийн хэмжээ $\fbox{abc}^\circ$, түүний эсрэг талын урт
$\fbox{d}$ байна.
$\vec p$, $\vec q$ нь $|\vec p+\vec q|=\sqrt3$ байх нэгж
векторууд бол $3\vec p-4\vec q$, $2\vec p+5\vec q$ векторуудын
скаляр үржвэр $-\dfrac{\fbox{ab}}2$ байна.
$\vec p$, $\vec q$ нь хоорондоо $\varphi$ өнцөг үүсгэх ижил
урттай векторууд ба $\vec p+3\vec q$, $5\vec p+3\vec q$ векторууд
перпендикуляр бол $\cos\varphi=-\dfrac{\fbox{a}}{\fbox{b}}$ байна.
$A(1;-6;0)$ цэгтэй, $B(3;2;-2)$ цэгийг дайрсан шулуунуудын
хувьд тэгшхэмтэй байрлах цэгүүдийн геометр байр нь
$(x-\fbox{a})^2+(y-\fbox{b})^2+(z+\fbox{c})^2=\fbox{de}$ тэгшитгэлтэй
бөмбөрцөг байна.
$A(-3;2;2)$ цэгтэй, $B(1;0;-2)$ цэгийг дайрсан хавтгайнуудын
хувьд тэгшхэмтэй байрлах цэгүүдийн геометр байр нь
$(x-\fbox{a})^2+(y-\fbox{b})^2+(z+\fbox{c})^2=\fbox{de}$ тэгшитгэлтэй
бөмбөрцөг гадаргуу үүсгэнэ.
$A(-1;0;2)$ цэгээс $B(3;-2;-2)$ цэгийг дайрсан шулуунуудад
буулгасан перпендикуляруудын суурийн геометр байр нь
$(x-\fbox{a})^2+(y+\fbox{b})^2+(z-\fbox{c})^2=\fbox{d}$ тэгшитгэлтэй
бөмбөрцөг гадаргуу байна.
$A(1;2;-3)$ цэгээс $B(5;4;1)$ цэгийг дайрсан хавтгайнуудад
буулгасан перпендикуляруудын суурийн геометр байр нь
$(x-\fbox{a})^2+(y-\fbox{b})^2+(z+\fbox{c})^2=\fbox{d}$ тэгшитгэлтэй
бөмбөрцөг гадаргуу үүсгэнэ.
Гурвалжин пирамид $OABC$-ийн $OA$ ирмэгийн дундаж цэг $D$,
$OBC$ талсын медиануудын огтлолцлын цэг $E$ бол $\overrightarrow{OA}=\vec a$,
$\overrightarrow{OB}=\vec b$, $\overrightarrow{OC}=\vec c$ векторуудаар
$\overrightarrow{DE}=\displaystyle\frac1{\fbox{a}}(-\fbox{b}\vec a+\fbox{c}\vec
b+\fbox{d}\vec c)$ гэж задарна.
$OABC$ пирамидийн $OA$ ирмэгийн дундаж цэг $D$, $ABC$
талсын медиануудын огтлолцлын цэг $E$ бол $\overrightarrow{AO}=\vec a$,
$\vec{AB}=\vec b$, $\overrightarrow{AC}=\vec c$ векторуудаар
$\overrightarrow{DE}=-\displaystyle\frac1{\fbox{a}}\vec
a+\displaystyle\frac1{\fbox{b}}\vec
b+\displaystyle\frac1{\fbox{c}}\vec c$ гэж задрана.
$\vec a+\vec b+\vec c=0$ ба $|\vec a|=1$, $|\vec b|=3$,
$|\vec c|=4$ бол $\vec a\vec b+\vec a\vec c+\vec b\vec c=\fbox{abc}$
байна (6 оноо)
$ABC$ гурвалжны хувьд $\overrightarrow{AB}=\vec a$, $\overrightarrow{BC}=\vec b$,
$\overrightarrow{CA}=\vec c$ ба $|\vec a|=|\vec b|=2\sqrt5$, $|\vec c|=6$ бол
$\vec a\vec b+\vec a\vec c+\vec b\vec c=\fbox{abc}$ байна.
$A(1;3)$, $B(-5;6)$ цэгүүд хүрэх зайнуудын нийлбэр нь
хамгийн бага байх $Ox$ тэнхлэгийн цэг $C(-\fbox{a};0)$, $AC$
шулууны тэгшитгэл $\fbox{b}x-\fbox{c}y+3=0$ байна.
$A(1;3)$, $B(-4;2)$ цэгүүд хүрэх зайнуудын нийлбэр нь
хамгийн бага байх $Ox$ тэнхлэгийн цэг $C(-\fbox{a};0)$, $BC$
шулууны тэгшитгэл $\fbox{b}x+\fbox{c}y+2=0$ байна.
Гэрлийн туяа $Ox$, $Oy$ тэнхлэгүүдэд тусахдаа тэдгээрээс
ойдог гэж үзье. $A(6;2)$ цэгээс гарч $Ox$ тэнхлэгийн $B(\fbox{a};0)$
цэгээс, дараа нь $Oy$ тэнхлэгийн $C(0;\fbox{b})$ цэгээс ойсон
гэрлийн туяа $D(3;4)$ цэгийг дайрах ба $BC$ шулууны тэгшитгэл
$\fbox{c}x+\fbox{d}y-6=0$ байна.
Гэрлийн туяа $Ox$, $Oy$ тэнхлэгүүдэд тусахдаа тэдгээрээс
ойдог гэе. $A(6;6)$ цэгээс гарсан гэрлийн туяа эхлээд
$B(\fbox{a};0)$ цэгээс ойж, дараа нь $C(0;\fbox{b})$ цэгээс ойхдоо
$D(2;6)$ цэгийг дайрах ба $\fbox{c}x+\fbox{d}y-6=0$ тэгшитгэлээр $BC$
шулуун тодорхойлогдоно.
$A(\fbox{a},\fbox{b},\fbox{c})$ цэг $x+y+z-3=0$ хавтгайн хувьд
координатын эхтэй тэгш хэмтэй байрлана.
$A(\fbox{ab};\fbox{c};\fbox{d})$ цэг $x-y-z+3=0$ хавтгайн хувьд
координатын эхтэй тэгшхэмтэй байрлана.
$\vec a=\vec i-\vec j+2\vec k$, $\vec b=3\vec i+\vec j$,
$\vec c=\fbox{a}\vec i+2\vec k$ векторууд компланар байхад
$\cos(\vec b\stackrel{^\land}{,}\vec
c)=\displaystyle\frac{\fbox{b}}{\fbox{c}\sqrt{2}}$ байна.
$\vec a=\vec i+\vec j+\vec k$, $\vec b=\vec i+3\vec j-\vec
k$, $\vec c=-\fbox{a}\vec j+2\vec k$ векторууд компланар байхад
$\vec c$ вектор $Oy$ тэнхлэгтэй
$\displaystyle\frac{\fbox{b}}{\fbox{c}}\cdot\pi$ өнцөг үүсгэнэ
$(\fbox{c}< 7)$.
$ABCD$ зөв тетраэдрийн $ABD$ талсын хүндийн төвийг $M$ гэвэл
$\overrightarrow{CA}=\vec p$, $\overrightarrow{CB}=\vec q$, $\overrightarrow{CD}=\vec r$
векторуудын хувьд $\overrightarrow{CM}=\dfrac{\fbox{a}}{\fbox{b}}(\vec p+\vec
q+\vec r)$ байх ба $\overrightarrow{CM}$, $\overrightarrow{BD}$ векторуудын хоорондох
өнцөг $\fbox{cd}^\circ$ байна.
Бүх ирмэг нь ижил урттай зөв дөрвөн өнцөгт пирамид $SABCD$-ийн $SC$ ирмэг дээр $SM:MC=3:1$ байх $M$ цэг авч $\overrightarrow{AD}=\vec p$, $\overrightarrow{AB}=\vec q$, $\overrightarrow{AS}=\vec r$ гэвэл $\overrightarrow{AM}=\dfrac14(\fbox{a}\vec p+3\vec q+\fbox{b}\vec r)$ байх ба
$\overrightarrow{AM}$, $\overrightarrow{BD}$ векторуудын хоорондох өнцөг $\fbox{cd}^\circ$ байна.
$ABC$ гурвалжны $AB$ тал дээр $AN=3NB$ байх $N$ цэг авч $AM$
медиан $CN$ хэрчимтэй огтлолцох цэгийг $O$ гэе. $\overrightarrow{AM}=\vec p$,
$\overrightarrow{CN}=\vec q$ векторуудаар
$\overrightarrow{AB}=\dfrac{\fbox{a}}{\fbox{b}}(2\vec p+\vec q)$ гэж задрах ба
$AM=CN=7$, $\measuredangle NOM=60^\circ$ бол $AB=\fbox{c}\sqrt{\fbox{d}}$ байна.
$ABCD$ параллелограммын $BC$, $CD$ талуудын дундаж цэгийг
харгалзан $K$, $M$ гэвэл $\overrightarrow{AK}=\vec p$, $\overrightarrow{AM}=\vec q$
векторуудаар $\overrightarrow{AD}=\dfrac{\fbox{a}}{\fbox{b}}(2\vec q-\vec p)$
гэж задрах ба $AK=6$, $AM=3$, $\widehat{KAM}=60^\circ$ бол
$AD=\fbox{c}$ байна.
$ABCD$ гүдгэр дөрвөн өнцөгтийн $AC$, $BD$ диагоналиудын
огтлолцлын цэг $O$-ийн хувьд $AO=OC=2$, $BO=1$, $OD=4$,
$\widehat{BOC}=60^\circ$ байв. Тэгвэл $CD=\fbox{a}\cdot AB$ ба
$\cos(\overrightarrow{AB}\stackrel{^\land}{,}\overrightarrow{DC})=\dfrac{\fbox{bc}}{14}$
байна.
$ABCD$ дөрвөн өнцөгтийн $A$ оройн өнцөг $120^\circ$ ба $AC$
диагональ энэ өнцгийн биссектрис болно. $AB=5AC$, $AD=3AC$ байсан
бол $CD^2=\fbox{a}AC^2$ ба
$\cos(\overrightarrow{BA}\stackrel{^\land}{,}\overrightarrow{CD})=\frac{\fbox{b}}{\fbox{c}}$
байна.
Координатын тэнхлэгүүд ба $3x-y+6=0$ шулуунаар хязгаарлагдсан
гурвалжны талбай $\fbox{a}$ кв.нэгж, багтаасан тойргийн тэгшитгэл
$(x+1)^2+(y-\fbox{b})^2=\fbox{cd}$ байна.
$3x+4y-12=0$ шулуун ба координатын тэнхлэгүүдээр хязгаарлагдсан гурвалжны талбай $\fbox{a}$ кв.нэгж, түүнд багтсан тойргийн радиус $\fbox{b}$ нэгж байна.
$x^2+y^2=9$ тэгшитгэлтэй тойрогт $A(0;5)$ цэгээс татсан
шүргэгчүүдийн тэгшитгэл $\fbox{a}x+\fbox{bc}y+15=0$,
$\fbox{d}x+\fbox{e}y-15=0$ байна.
$ABCA_1B_1C_1$ призмийн талсуудын $AB_1$, $CA_1$ диагоналиуд
дээр харгалзан байрлах $E,F$ цэгүүдийн хувьд $EF\|BC_1$ нөхцөл
биелнэ. $\overrightarrow{CA}=\vec a$, $\overrightarrow{CB}=\vec b$, $\overrightarrow{CC_1}=\vec c$
гэвэл $\overrightarrow{AB_1}=\fbox{a}\vec a+\vec b+\fbox{b}\vec c$,
$\overrightarrow{CA_1}=\vec a+\fbox{c}\vec b+\vec c$, $\overrightarrow{BC_1}=-\vec
b+\fbox{d}\vec c$ ба $EF:BC_1=\fbox{e}:\fbox{f}$ байна.
$ABCDA_1B_1C_1D_1$ параллелепипедийн талсуудын $AC$, $DC_1$
диагоналиуд дээр харгалзан $M,N$ цэгүүдийг $MN\|BD_1$ байхаар
авав. $\overrightarrow{CD}=\vec a$, $\overrightarrow{CB}=\vec b$, $\overrightarrow{CC_1}=\vec c$
гэвэл $\overrightarrow{BD_1}=\vec a+\fbox{a}\vec b+\vec c$, $\overrightarrow{CA}=\vec
a+\vec b+\fbox{b}\vec c$ ба $MN:BD_1=\fbox{c}:\fbox{d}$ болно.
$ABCD$ параллелограммын $BC$ тал дээр $BE:EC=2:1$ байх $E$
цэг, $CD$ тал дээр $CF:FD=1:3$ байх $F$ цэг авч $ED$, $AF$
хэрчмүүдийн огтлолцлын цэгийг $O$ гэвэл $EO:OD=\fbox{a}:\fbox{b}$,
$AO:OF=\fbox{c}:\fbox{d}$ байна.
$ABCD$ параллелограммын $BC$ тал дээр $BE:EC=1:2$ байх $E$
цэг, $CD$ тал дээр $CF:FD=2:3$ байх $F$ цэг авч $ED$, $AF$
шулуунуудын огтлолцлын цэгийг $O$ гэвэл $EO:OD=\fbox{a}:\fbox{b}$,
$AO:OF=\fbox{c}:\fbox{d}$ байна.
$5x-2y+9=0$ шулуун дээр орших $A(-\fbox{a};\fbox{b})$ цэг
$B(-2;-3)$, $C(4;1)$ цэгүүдээс ижил зайд байрлах ба $ABC$
гурвалжны талбай $\fbox{cd}$ байна.
$5x-2y+6=0$ шулуун дээр орших $A(\fbox{a};\fbox{b})$ цэг
$B(2;-1)$, $C(4;5)$ цэгүүдээс ижил зайд байрлах ба $ABC$ гурвалжны
талбай $\fbox{cd}$ байна.
$\alpha$ талтай квадратад багтсан тойргийн ямарч цэгээс
квадратын оройнууд хүрэх зайн квадратуудын нийлбэр тогтмол
$\fbox{a}\alpha^2$ байна.
$\alpha$ талтай квадрат багтаасан тойргийн ямарч цэгээс
квадратын оройнууд хүрэх зайн квадратуудын нийлбэр тогтмол
$\fbox{a}\alpha^2$ байна.
$ABC$ гурвалжны $AB$, $BC$, $CA$ талуудын дундаж цэгийг
харгалзан $M_1,M_2,M_3$ гэвэл энэ гурвалжны хавтгайд
$\overrightarrow{MA}+2\overrightarrow{MB}+3\overrightarrow{MC}=0$ нөхцлийг хангах $M$ цэг
$M_{\fbox{a}}M_{\fbox{b}}$ хэрчим дээр $M_{\fbox{a}}M:MM_{\fbox{b}}=\fbox{c}:\fbox{d}$ гэж байрлана ($\fbox{c}< \fbox{d}$).
$ABC$ гурвалжны $AB$, $BC$, $CA$ талуудын дундаж цэгийг
харгалзан $M_1,M_2,M_3$ гэвэл $4\overrightarrow{MA}+3\overrightarrow{MB}+\overrightarrow{MC}=0$
байхаар энэ гурвалжны хавтгайд байрлах $M$ цэг $M_{\fbox{a}}M_{\fbox{b}}$ хэрчмийг $M_{\fbox{a}}M:MM_{\fbox{b}}=\fbox{c}:\fbox{d}$ гэж хуваана ($\fbox{c}< \fbox{d}$).
$ABC$ гурвалжны $AB$, $BC$, $CA$ талууд дээр харгалзан
$P,Q,R$ цэгүүдийг
$\displaystyle\frac{AP}{AB}=\displaystyle\frac{BQ}{BC}=\displaystyle\frac{CR}{CA}$
байхаар авав. хэрэв $O$ нь $PQR$ гурвалжны медиануудын огтлолцлын
цэг ба $AO$ шулуун $BC$ талыг $H$ цэгээр огтолдог, $\overrightarrow{AB}=\vec
a$, $\overrightarrow{AC}=\vec b$ байсан бол
$\overrightarrow{AO}=\displaystyle\frac{\fbox{a}}{\fbox{b}}(\vec a+\vec b)$,
$BH:BC=\fbox{c}:\fbox{d}$ байна.
$ABC$ гурвалжны $AB$, $BC$, $CA$ талууд дээр харгалзан
$P,Q,R$ цэгүүдийг
$\displaystyle\frac{AP}{AB}=\displaystyle\frac{BQ}{BC}=\displaystyle\frac{CR}{CA}$
байхаар авав. $ABC$, $PQR$ гурвалжнуудын медиануудын огтлолцлын
цэг харгалзан $O,O_1$, $\overrightarrow{AB}=\vec a$, $\overrightarrow{AC}=\vec b$ гэвэл
$\overrightarrow{AO}=\displaystyle\frac{\fbox{a}}{\fbox{b}}(\vec a+\vec b)$,
$\overrightarrow{AO_1}=\displaystyle\frac{\fbox{c}}{\fbox{d}}(\vec a+\vec b)$
байна.
$ABC$ гурвалжны хувьд $AC=1$, $BC=2$, $\cos\hat
C=\displaystyle\frac34$ байхад $\vec a=\overrightarrow{CA}$, $\vec
b=\overrightarrow{CB}$ векторуудаар гурвалжны өндрүүдтэй давхцах $\overrightarrow{CD}$,
$\overrightarrow{AE}$ векторууд
$\overrightarrow{CD}=\displaystyle\frac1{\fbox{a}}(\fbox{b}\vec a-\vec b)$,
$\overrightarrow{AE}=-\vec a+\displaystyle\frac{\fbox{c}}{\fbox{d}}\vec b$ гэж
задарна.
$ABC$ гурвалжны хувьд $\overrightarrow{CA}=\vec a$, $|\vec a|=2$,
$\overrightarrow{CB}=\vec b$, $|\vec b|=3$, $\cos \hat
C=\displaystyle\frac34$ байв. Гурвалжны $CD$, $AE$ өндрүүдтэй
давхцах векторууд $\vec a,\vec b$ векторуудаар
$\overrightarrow{CD}=\displaystyle\frac1{\fbox{a}}(\fbox{b}\vec a-\vec b)$,
$\overrightarrow{AE}=-\vec a+\displaystyle\frac{\fbox{c}}{\fbox{d}}\vec b$ гэж
илэрхийлэгдэнэ.
Координатууд $(x;y)$ нь $2|x|+|y+2x+1|\le5$ нөхцлийг хангах
цэгүүдээс тогтох $Oxy$ хавтгайн муж нь $y=\fbox{a}$, $y=-6$,
$4x+y-\fbox{b}=0$, $4x+y+\fbox{c}=0$ шулуунуудаар хүрээлэгдсэн
параллелограмм байх ба түүний талбай $S=\fbox{de}$ болно.
$Oxy$ хавтгайн, $|y-2x|+2|x|\le3$ нөхцлийг хангах
координаттай цэгүүдийн байр нь $y=\fbox{a}$, $y=-3$, $\fbox{b}x-y=3$,
$y-4x=\fbox{c}$ тэгшитгэлтэй шулуунуудаар хүрээлэгдсэн $S=\fbox{d}$
талбайтай параллелограмм байна.
$a$ ирмэгтэй $ABCDA_1B_1C_1D_1$ кубийн $AA_1$, $BC$, $C_1D_1$
ирмэгүүд дээр харгалзан байрлах $P,Q,R$ цэгүүдийн хоорондох зайн
квадратуудын нийлбэрийн хамгийн бага утга нь
$\displaystyle\frac{\fbox{a}}{\fbox{b}}a^2$ байх ба энэ үед
$AP:PA_1=\fbox{c}:\fbox{d}$ юм.
Тэгш өнцөгт параллелепипед $ABCDA_1B_1C_1D_1$-ийн ирмэгүүд
$AA_1=a$, $BC=b$, $C_1D_1=c$ бол эдгээр ирмэгүүд дээр харгалзан
байрлах $P,Q,R$ цэгүүдийн хоорондох зайн квадратуудын нийлбэрийн
хамгийн бага утга нь
$\displaystyle\frac{\fbox{a}}{\fbox{b}}(a^2+b^2+c^2)$ байх ба энэ үед
$AP:PA_1=\fbox{c}:\fbox{d}$ болно.
$ABC$ гурвалжны $BM$ медиан $AL$ биссектристэй перпендикуляр
ба $BM:AL=1:2$ байв. $\overrightarrow{AC}=2\vec a$, $\overrightarrow{AB}=\vec b$ гэвэл
$AL^2=\displaystyle\frac{\fbox{a}}{9}\vec a ^2(1+\cos\hat A)$,
$BM^2=\fbox{b}\vec a ^2(1-\cos\hat A)$ байх тул $\cos\hat
A=\displaystyle\frac{\fbox{c}}{\fbox{d}}$ болно.
$ABC$ гурвалжны $CM$ медиан $AL$ биссектристэй перпендикуляр
ба $CM:AL=3:4$ байв. $\overrightarrow{AB}=2\vec b$, $\overrightarrow{AC}=\vec c$ гэвэл
$AL^2=\displaystyle\frac{\fbox{a}}9\vec b ^2(1+\cos\hat A)$,
$\overrightarrow{CM}^2=\fbox{b}\vec b ^2(1-\cos\hat A)$ байх тул $\cos\hat
A=\displaystyle\frac{\fbox{c}}{\fbox{d}}$ байна.
Гурвалжин пирамид $ABCD$-ийн $AB$, $CD$, $BC$ ирмэгүүд дээр
харгалзан $M,N,Q$ цэгүүдийг $AM=MB$, $CN=ND$, $CQ:QB=2:3$ байхаар
аваад $MQ$, $AC$ шулуунуудын огтлолцлын цэгийг $S$ гэвэл
$\overrightarrow{SC}=\fbox{a}\overrightarrow{CA}$ болох ба $M,N,Q$ цэгүүдийг дайрсан
хавтгай $AD$ ирмэгийг $AP:PD=\fbox{b}:\fbox{c}$ байх $P$ цэгээр
огтолно.
$ABCD$ пирамидын $AB$, $CD$ ирмэгүүдийн дундаж цэгийг
харгалзан $M,N$ гээд $DA$ ирмэг дээр $DP:PA=2:3$ байх $P$ цэг
авахад $M,N,P$ цэгүүдийг дайрсан хавтгай $AC$ шулууныг $S$, $CB$
ирмэгийг $Q$ цэгээр огтолбол $\overrightarrow{SC}=\fbox{a}\overrightarrow{CA}$,
$CQ:QB=\fbox{b}:\fbox{c}$ байна.
$ABCDA_1B_1C_1D_1$ параллелепипедийн $BC$ ирмэгийн дундаж
цэг $M$-ийг дайрч $AC_1$, $DD_1$ шулуунуудыг харгалзан $N,P$
цэгүүдээр огтолсон шулуун оршин байх ба
$\overrightarrow{AN}=\dfrac2{\fbox{a}}\overrightarrow{AC_1}$,
$\overrightarrow{DP}=\fbox{b}\overrightarrow{DD_1}$, $MN:NP=\fbox{c}:\fbox{d}$ болно.
$ABCDA_1B_1C_1D_1$ параллелепипедийн $B,D,A_1$ оройнуудыг
дайрсан хавтгай түүний $AC_1$ диагоналийг $F$ цэгээр огтолдог ба
$\overrightarrow{AB}=\vec a$, $\overrightarrow{AD}=\vec b$, $\overrightarrow{AA_1}=\vec c$ гэвэл
$\overrightarrow{DF}=\displaystyle\frac13(\fbox{a}\vec a-\fbox{b}\vec b+\vec c)$,
$AF:FC_1=\fbox{c}:\fbox{d}$ болно.
$a$ урттай ирмэг бүхий кубийн зэргэлдээ хоёр талсын солбисон
диагоналиудын хоорондох зайг $\delta$ гэе. Эдгээр диагоналийн
ерөнхий перпендикуляр хэрчим диагоналийг $\fbox{a}:\fbox{b}$ $(a< b)$
харьцаагаар хуваах ба
$\delta=\displaystyle\frac{\sqrt{\fbox{c}}}3\,a$ байна.
Бүх ирмэг нь $a$ урттай зөв гурвалжин призмийн зэргэлдээ
хоёр хажуу талсын солбисон диагоналиудын хоорондох зайг $\delta$
гэе. Эдгээр диагоналийн ерөнхий перпендикуляр хэрчим диагоналийг
$\fbox{a}:\fbox{b}$ $(a< b)$ харьцаагаар хуваах ба
$\delta=\displaystyle\frac{\sqrt{\fbox{c}}}5\,a$ байна.
$A(2;-3;5)$, $B(1;0;8)$, $C(-2;4;1)$ цэгүүд өгөгдөв. $\overrightarrow{CD}=-3\overrightarrow{AB}$ байх $D$ цэгийн координат нь $(\fbox{a};\fbox{bc};\fbox{de})$ ба энэ цэгийн координатуудын нийлбэр нь $\fbox{fgh}$ байна.
$ABCD$ пирамидын $AB, CD$ ирмэгүүдийн дундаж цэгийг харгалзан $M, N$ гээд $DA$ ирмэг дээр $DP:PA=3:2$ байх $P$ цэг авахад $M, N, P$ цэгүүдийг дайрсан хавтгай $AC$ шулууныг $S$, $CB$ ирмэгийг $Q$ цэгээр огтолбол $\overrightarrow{SC}=\fbox{a}\overrightarrow{AC}$, $CQ:QB=\fbox{b}:\fbox{c}$ байна.
- $\vec{\mathstrut{a}}=(-3, 2)$, $\vec{\mathstrut{b}}=(1, 1)$ векторууд өгөгдөв. $2\vec{\mathstrut{a}}-3\vec{\mathstrut{b}}$ векторын координат нь $(-\fbox{a};\fbox{b})$ ба урт нь $\sqrt{\fbox{cd}}$ байна.
- $\vec{\mathstrut{p}}=(-7, 2)$, $\vec{\mathstrut{x}}=(1, a)$, $\vec{\mathstrut{y}}=(b, 2)$ ба $\vec{\mathstrut{p}}=2\vec{\mathstrut{x}}-3\vec{\mathstrut{y}}$ нөхцөлийг хангах бол $a=\fbox{e}, b=\fbox{f}$ байна.
- $\vec{\mathstrut{u}}=(3,-4)$ вектортой параллел нэгж вектор нь $\dfrac{1}{\fbox{g}}\vec{\mathstrut{u}}$ байна.
Координатын аргын үндсэн томьёонууд
$A(2,-1)$, $P(-1,1)$ цэгүүд өгөгдөв. $A$ төвтэй төвийн тэгш хэмээр $P$ цэг $Q$-д буусан бол $Q$ цэгийн координат $(p,q)$-г ол.
Координатын хавтгайд $A(1,2)$, $B(5,4)$, $C(3,6)$, $D(x,y)$ цэгүүд өгөгдөв.
- Эдгээр цэгүүд параллелограммын дөрвөн орой үүсгэх $D$ цэгийн координатыг ол.
- $AD^2+BD^2+CD^2$ хамгийн бага байх $D$ цэгийн координатыг ол.
$x^2+y^2=4 \boldsymbol{\cdots}(1)$, $x^2+y^2-8x-4y+4=0 \boldsymbol{\cdots}(2)$ тойргуудын хувьд дараах acуултанд хариул.
- Хоёр тойрог огтлолцох эсэхийг шинжил.
- Хоёр тойргийн огтлолцлын цэгийн координатыг ол.
$(x-a\cos\theta)^2+(y-a\sin \theta)^2=1$ ($a$ нь $0< a< 1$ тогтмол
тоо) тойрог $OX$ тэнхлэгийг $A$ ба $C$, $OY$-тэнхлэгийг $B, D$
цэгүүдээр огтлох ба $A$ цэгийн абсцисс, $B$-ийн ординат эерэг.
- $ABCD$ дөрвөн өнцөгтийн талбайг $a$ ба $\theta$-өөр илэрхийл.
- $\theta$ нь $0^{\circ}< \theta< 90^{\circ}$ мужаар хөдөлж байх үед $S_{ABCD}$-ийн хамгийн их утгыг ол. $\max (S_{ABCD})$ үеийн $\theta$-ийн утгыг ол.
Дараах нөхцлийг хангах шулууны тэгшитгэлийг бич.
- $(-1,3)$ цэгийг дайрсан $-2$ өнцгийн коэффициенттэй;
- $(1,-2)$ ба $(-3,4)$ цэгүүдийг дайрсан;
- $(4,1)$ ба $(4,5)$ цэгүүдийг дайрсан;
- $(3,-2)$ цэгийг дайрсан $4x-5y+3=0$ шулуунтай параллель;
- $P(-1,2)$, $Q(1,-3)$ цэгүүд өгөгдөв. $PQ$-ийн дундаж цэгийг дайрсан $PQ$-д перпендикуляр шулуун.
Координатын шулуун дээр $A(-2)$, $B(1)$, $C(5)$ цэгүүд өгөгдөв.
- $AB$, $CA$ хэрчмүүдийн уртыг ол.
- $AB$ хэрчмийг $3:2$ харьцаагаар хуваах $P$, $3:2$ харьцаагаар гадаад байдлаар хуваах $Q$, $2:3$ харьцаагаар гадаад байдлаар хуваах $R$ цэгүүдийг ол.
Гурвалжны гурван өндөр нэг цэгт огтлолцохыг батал.
$O(0, 0)$ ба $O$-г дайрсан
шулуун дээр $O$-ийн нэг талд орших $P(x, y)$, $Q(X, Y)$ цэгүүдийн
хувьд $OP\cdot OQ=2$ байв.
- $x, y$-ийг $X, Y$-ээр илэрхийл.
- $P$ цэг $x+2y=1$ шулуунаар хөдлөхөд $Q$ цэгийн геометр байрыг ол.
$A(5,4), B(0,-1), C(8,-2)$ цэгүүд өгөгдөв.
- $AB$ хэрчмийг дотоод байдлаар $3:2$ харьцаагаар хуваах $P$ цэг, $3:2$ харьцаагаар гадаад байдлаар хуваах $Q$ цэгүүдийг ол.
- $\triangle ABC$-ийн хүндийн төв $G$ цэгийг ол.
- $\triangle PQR$-ийн хүндийн төв $G$ бол $R$ цэгийг ол.
$P: y=x^2+kx+1, A(2,1), B(4,7)$ гэе.
- $A, B$ цэгүүд $P$ муруйгаар таслагдсан хавтгайн өөр өөр хэсгүүдэд байх $k$-г ол.
- $AB$ хэрчим $P$ муруйтэй ерөнхий цэгтэй байх $k$-г ол.
Координатын хавтгайд $O(0, 0)$ , $A(1, 3)$, $B(5, 6)$, $C(-2, 7)$, $D(t, 0) [t>0]$ цэгүүд өгөгдөв.
- $O$ ба $A$, $A$ ба $B$ цэгүүдийн хоорондын зайг ол.
- $\triangle ABC $ тэгш өнцөгт гэдгийг харуул.
- $\triangle ABD$ нь адил хажуут байх $t$-г ол.
$A(3, 5)$, $B(5, 2)$, $C(1, 1)$ цэгүүдээр тодорхойлогдох $\triangle ABC$ гурвалжны талбайг ол.
$\triangle ABC$-ийн $BC$ талын дундаж нь $M$ цэг бол $$AB^2+AC^2=2(AM^2+BM^2)$$ гэж батал.
$m, n>0$ ба $AB$ хэрчмийг $m:n$ харьцаагаар хуваасан цэг нь $C$, $BC$ хэрчмийг $m:n$ харьцаагаар гадаад байдлаар хуваах цэг нь $A$ бол $m:n$-г ол.
$\triangle ABC$-ийн $BC$, $CA$, $AB$ талуудыг ижил харьцаагаар хуваах цэгүүдийг харгалзан $L$, $M$, $N$ гэе. $\triangle LMN$-ийн хүндийн төв нь $\triangle ABC$-ийн хүндийн төвтэй давхцахыг харуул.
Координатын хавтгайд $A(3, 4)$,
$B(-3, 1)$, $C(5,-2)$ цэгүүд өгөгдөв. $AB$ хэрчмийг $2:1$ харьцаанд
хуваах цэг $D$, $AC$ хэрчмийн үргэлжлэлийг $3:1$ харьцаанд хуваах
цэг $E$ бол $DE$ хэрчмийг $3:4$ харьцаанд хуваах цэгийн
координатыг ол.
$P(1,2)$ цэг ба $\ell\colon 3x+4y-15=0$, $m\colon x+2y-5=0$ шулуунууд өгөгдөв.
- $\ell$ шулууны хувьд $P$-тэй тэгш хэмтэй $Q$ цэгийн координатыг ол.
- $\ell$ шулууны хувьд $m$-тэй тэгш хэмтэй шулууныг ол.
$A(2\sqrt{3}, 1)$, $B(-\sqrt{3},-2)$, $C(\sqrt{3}-1,\sqrt{3})$ байх $ABC$ гурвалжны талбайг ол.
$A(0, 2)$, $B(-1,-1)$, $C(3, 0)$, $D(x, y)$ дөрвөн цэг параллельограммын оройнууд бол $D$ цэгийн координатыг ол.
Координатын шулуун дээр $A(-3), B(5), C$ цэгүүд ба $AB$ хэрчмийг дотоод байдлаар $2:1$ харьцаагаар хуваах $P$ цэг, гадаад байдлаар $2:1$ харьцаагаар хуваах $Q$ цэгүүд өгөгдөв.
- $AB$ хэрчмийн урт ба $P, Q$ цэгүүдийн координатыг ол.
- $AC$ хэрчмийг гадаад байдлаар $5:1$ харьцаагаар хуваах цэг нь $B$ бол $C$-ийн координатыг ол.
$O(0, 0), A(3,-4), B(8, 6), C(-1, 0)$ бол $OA$, $AB$, $BC$ хэрчмүүдийн уртыг ол.
$A(1, 1)$, $B(3, 0)$ цэгүүд хүртэлх зай нь тэнцүү байx $y=3x$ шулууны $P$ цэгийн координатыг ол.
$A(4, 0)$, $B(0, 2)$, $C$ цэгүүд зөв гурвалжин үүсгэх бол $C$ оройг ол.
$AB$ хэрчмийг дотоод, гадаад байдлаар $2:5$ харьцаагаар хуваах цэгүүд болон гадаад байдлаар $5:2$ харьцаагаар хуваах цэгүүдийн координатыг ол. $A(x_1, y_1)$, $B(x_2,y_2)$ гэж үз.
Координатын хавтгайд $A(3, 3), B(1, 2), C(4, 0)$ цэгүүд өгөгдөв.
- $\triangle ABC$-ийн хүндийн төв $G$-ийн координатыг ол.
- $\triangle BCD$-ийн хүндийн төв $A$ бол $D$-ийн координатыг ол.
$\triangle ABC$-ийн $BC$, $CA$, $AB$ талуудыг харгалзан $1:1, 2:1, 2:3$ харьцаагаар дотоод байдлаар хуваах цэгүүд нь $P(5, 2)$, $Q(7, 8)$, $R(4, 6)$ бол $A$, $B$, $C$-г ол.
Хавтгайн дурын $P$ цэг ба $ABCD$ тэгш өнцөгтийн хувьд $$PA^2+PC^2=PB^2+PD^2$$ болохыг батал.
Гурвалжны 3 медиан нэг цэгт огтолцохыг батал.
Хавтгайн $A(3, 3), B(1, 2), C(4, 0)$ цэгүүдээс ижил зайд алслагдах
$P$ цэгийн координатыг ол. Энэ цэг нь $\triangle ABC$-г багтаасан тойргийн төв болно.
$A(2, 3)$ төвтэй төвийн тэгш хэмээр $P(0, 2)$ цэг $Q$-д буусан бол $Q$-ийн координатыг ол.
$y=2x^2-12x+23$ параболын оройн цэг нь $(2,-3)$ төвтэй тэгш хэмээр ямар координаттай цэгт буух вэ?
$A(1, 4), B(-2,-1), C(4, 0)$ байв. $P$ цэгт төвтэй төвийн тэгш хэмээр $\triangle ABC$, $\triangle A'B'C'$-д буусан ба $\triangle A'B'C'$-ийн хүндийн төв $(6,8)$ координаттай бол $\triangle A'B'C'$-ийн 3 оройн координатыг ол.
$ABCD$ параллелограммын хувьд $AB=5, BC=6$, $AC:BD=1:2$ бол $BD$ диагоналын уртыг ол.
$A(x_1,y_1)$, $B(x_2,y_2)$, $C(x_3,y_3)$ цэгүүдийн хувьд $DA^2+DB^2+DC^2$ нийлбэр хамгийн бага байх $D$ цэгийн координатыг ол.
Гурвалжны талуудын дундажуудыг дайруулан уг талдаа перпендикуляр шулуунууд татав. Эдгээр шулуунууд нэг цэгт огтлолцохыг батал.
Дараах цэгүүдэд оройтой гурвалжны талбайг ол.
- $O(0, 0)$, $A(-2,1)$, $B(1, 2)$;
- $A(-3,-2)$, $B(1, 4)$, $C(-1, 7).$
$x-4y=-3$, $2x-y=1$, $3x+2y=14$ шулуунуудын огтлолцолд үүсэх гурвалжны талбайг ол.
$A(1, 1)$, $B(3, 5)$, $C(5, 2)$ гурван цэг ба $y=2x^2-1$ парабол
дээр хөдөлж буй $P$ цэгүүд өгөгдөв.
- $S_{\triangle ABC}$-г ол.
- $A$ цэгийг дайрсан, $\triangle ABC$ гурвалжны талбайг хагаслан хуваах $\ell$ шулууны тэгшитгэлийг бич.
- $BC$ талтай параллель $m$-шулуун талбайг хагаслан хуваах бол тэгшитгэлийг бич.
- $A$, $B$, $P$ гурван цэг нэг шулуун дээр орших $P$-г ол.
$2x+y-3=0$, $x-2y+1=0$ шулуунуудын биссектрисүүдийг ол.
$y=x^2$ парабол дээр $A(a, a^2)$, $B(b, b^2)$, $C(c, c^2)$ цэгүүд авчээ. $AB$
шулууны өнцгийн коэффициент хоёр бол $\triangle ABC$ зөв гурвалжин
байх $a, b, c$-ийн утгыг ол.
$y=3x$ шулуун дээр орших $P$ цэгээс $A(1,1)$, $B(3,0)$ цэгүүд хүртэлх зай тэнцүү бол $P$ цэгийн координатыг ол.
$(1; -3)$, $(4; 1)$, $(7; y)$, $(x; 5)$ цэгүүд дараалсан оройнууд байх параллелограммын хувьд $x+y$-ийн утга аль вэ?
A. $8$
B. $9$
C. $10$
D. $11$
E. $13$
$7$ см талтай $ABCD$ квадратын $AD$ талын дундаж цэг $K$ болно. $CK$ шулууны дагуу цаасыг нугалж тэр хоёр талст өнцгийг $60^\circ$ болгов. $B$ ба $D$ цэгүүдийн хоорондох зайг ол.
A. $14\sqrt{5}$
B. $7\sqrt5$
C. $\frac{14\sqrt5}{5}$
D. $\frac{7\sqrt5}{5}$
E. $\frac{2\sqrt5}{5}$
$A(-2,4,6)$; $B(6,2,4)$; $C(1,-1,-3)$ цэгүүдэд оройтой $ABC$ гурвалжны $C$ оройгоос татсан медианы уртыг ол.
A. 4
B. 6
C. 8
D. 9
E. 10
Координатын хавтгайд $A(-1,1)$ ба $B(3,4)$ цэгүүд өгөв. $O(0,0)$ цэгээс $AB$ шулуун хүрэх хамгийн богино зайг ол.
A. $\dfrac85$
B. $1.4$
C. $\sqrt3$
D. $0.8$
E. $\sqrt2$
$A(1;3)$, $B(5;3)$, $C(1;6)$ бол $ABC$ тэгш өнцөгт гурвалжны гипотенузын дундаж цэгийг ол.
A. $(6;9)$
B. $(1;4.5)$
C. $(3;4.5)$
D. $\big(\frac{7}{3};4\big)$
E. $(3;3)$
$ABC$ гурвалжны $A(3;4)$, $B(3;7)$, $C(5;9)$ бол $AD$ медианы уртыг ол.
A. $4$
B. $\sqrt{17}$
C. $3\sqrt{2}$
D. $3\sqrt{3}$
E. $5$
$ABCD$ квадратын хувьд $A(4;1)$, $B(0;4)$, $C(-3;0)$ бол $D$ оройн координатыг ол.
A. $D(1;1)$
B. $D(1;-3)$
C. $D(1;-1)$
D. $D(2;-3)$
E. $D(2;-1)$
$OM=\sqrt2$, $ON=\sqrt8$, $MN=3\sqrt2$ бол аль цэг нөгөө
хоёрынхоо хооронд орших вэ?
A. $M$
B. $N$
C. $O$
D. аль нь ч биш
E. аль нь ч байж болно
$PQ=\sqrt3$, $QR=3\sqrt3$, $PR=\sqrt{12}$ байх гурван цэгийн
аль нь нөгөө хоёрын хооронд орших вэ?
A. $P$
B. $Q$
C. $R$
D. аль нь ч биш
E. аль нь ч байж болно
$(1;0)$, $(0;-3)$, $(0;3)$ цэгт оройтой гурвалжин ямар гурвалжин бэ?
A. адил хажуут
B. тэнцүү талт
C. элдэв талт
D. тэгш өнцөгт
E. аль нь ч биш
$(-7;0)$, $(0;-3)$, $(0;3)$ цэгийг холбоход ямар гурвалжин үүсэх бэ?
A. элдэв талт
B. тэнцүү талт
C. адил хажуут
D. тэгш өнцөгт
E. аль нь ч биш
$(3;0)$, $(0;-4)$ гэсэн 2 цэгийн хоорондох зай хэдэн нэгж
вэ?
A. $7$
B. $6.1$
C. $5$
D. $5.2$
E. $4.5$
$(-3;0)$, $(0;-4)$ хоёр цэгийн хоорондох зай аль вэ?
A. $5.2$
B. $7$
C. $6$
D. $5$
E. $3$
$M(-2;0)$, $N(7;0)$, $L(2;4)$. $MNL$ гурвалжны $ML$ суурьтай
параллель дундаж шугамын урт аль вэ?
A. $3$
B. $2\sqrt3$
C. $2\sqrt2$
D. $\sqrt5$
E. $3\sqrt{2}$
$L(2;4)$, $N(4;0)$, $M(-2;0)$. $LNM$ гурвалжны $LN$ суурьтай
параллель дундаж шугамын урт аль вэ?
A. $\sqrt3$
B. $5$
C. $3$
D. $\sqrt5$
E. $2$
$M_1(2;0;0)$, $M_2(0;2;0)$, $M_3(0;0;3)$. $M_1M_2M_3$
гурвалжны периметр аль вэ?
A. $\sqrt2+\sqrt3$
B. $\sqrt{15}$
C. $2(\sqrt{13}+\sqrt2)$
D. $2(\sqrt2+\sqrt{11})$
E. $7$
$M_1(1;0;0)$, $M_2(0;1;0)$, $M_3(0;0;2)$. $M_1M_2M_3$
гурвалжны периметр аль вэ?
A. $2+\sqrt{10}$
B. $\sqrt2(1+\sqrt{10})$
C. $\sqrt2(1+\sqrt5)$
D. $\sqrt2+\sqrt5$
E. $4$
$M(2,-1,-3)$ цэгтэй $xOy$ хавтгайн хувьд тэгш хэмтэй цэг аль вэ?
A. $(-2,-1,3)$
B. $(2,1,3)$
C. $(2,-1,3)$
D. $(-2,1,3)$
E. $(-2,1,-3)$
$M(2;-1;3)$ цэгтэй $xOz$ хавтгайн хувьд тэгш хэмтэй цэг аль
вэ?
A. $(2;-1;-3)$
B. $(2;1;3)$
C. $(2;1;-3)$
D. $(-2;1;3)$
$M(1;2;3)$, $N(3;4;-1)$. $MN$ хэрчмийн дундаж цэг аль вэ?
A. $(-2;3;1)$
B. $B(1;1;-2)$
C. $(2;3;1)$
D. $D(0;0;1)$
$MN$ хэрчмийн дундаж $K(0;2;3)$ ба $M(-2;3;1)$ бол $N$
цэгийн координат аль вэ?
A. $(1;2;5)$
B. $(2;5;1)$
C. $(5;2;1)$
D. $(2;1;5)$
$P(2;-1;3)$ цэгтэй $Oz$ тэнхлэгийн хувьд тэгш хэмтэй цэг аль
вэ?
A. $(2;-1;3)$
B. $(-2;1;3)$
C. $(2;1;3)$
D. $(2;-1;-3)$
$P(-2;1;3)$ цэгтэй $Oz$ тэнхлэгийн хувьд тэгш хэмтэй цэг аль
вэ?
A. $(2;1;3)$
B. $(-2;-1;3)$
C. $(2;-1;3)$
D. $D(2;1;-3)$
$P(4;3;-2)$ цэгээс $Oz$ тэнхлэг хүртэлх зай аль вэ?
A. $4$
B. $3$
C. $2$
D. $5$
$P(2;-3;4)$ цэгээс $Ox$ (абсцисс) тэнхлэг хүртэлх зай аль
вэ?
A. $5$
B. $3$
C. $4$
D. $2$
E. $2\sqrt{3}$
$P(3;4;2\sqrt6)$ цэгээс координатын эх хүртэлх зай аль вэ?
A. $6$
B. $5$
C. $7$
D. $8$
$P(4;\sqrt{23};5)$ цэгээс координатын эх хүртэлх зай аль вэ?
A. $7$
B. $8$
C. $9$
D. $6$
$A(3;3)$, $B(4;6)$, $C(13;3)$ цэгүүд дээр оройтой гурвалжны $B$ оройгоос татсан медианы уртыг ол.
A. $4$
B. $5$
C. $25$
D. $2\sqrt6$
E. $4.5$
$A(0;1)$, $B(1;4)$, $C(10;1)$ цэгүүд дээр оройтой гурвалжны
$B$ оройгоос татсан медианы уртыг ол.
A. $5$
B. $4$
C. $25$
D. $2\sqrt6$
E. $4.5$
$A(2;-3;-5)$, $B(-1;5;2)$, $C(3;-3;4)$ цэгүүдэд оройтой $ABC$ гурвалжны $A$ оройгоос татсан медианы уртыг ол
A. 4
B. 6
C. 8
D. 9
E. 10
$A(0;2)$, $B(1;5)$, $C(10;2)$ цэгүүд дээр оройтой гурвалжны $B$ оройгоос татсан медианы уртыг ол.
A. $4.5$
B. $4$
C. $25$
D. $2\sqrt6$
E. $5$
$A(2;3)$, $B(3;6)$, $C(12;3)$ цэгүүд дээр оройтой гурвалжны $B$ оройгоос татсан медианы уртыг ол.
A. $5$
B. $4$
C. $25$
D. $2\sqrt6$
E. $4.5$
$A(4,3)$, $B(-3,5)$, $C(0,-3)$ бол $\triangle ABC$-ийн талбайг ол.
A. 25
B. 26
C. 28
D. 30
E. 31
$ABC$ гурвалжны $A(-3;4)$ ба $B(1;6)$ бол $AC$ болон $CB$ талуудын дунджийг холбосон хэрчмийн уртыг олоорой.
A. $\sqrt5$
B. $3\sqrt2$
C. $2\sqrt3$
D. $2\sqrt2$
E. $2$
$A(5,4)$, $B(2,2)$, $C(-4,6)$ бол $ABC$ гурвалжны $AM$ медианы уртыг ол.
A. 2
B. 5
C. 6
D. 8
E. 10
$A(1,2)$, $B(5,-1)$ цэгүүдийн хоорондох зайг ол.
A. $5$
B. $25$
C. $\sqrt{31}$
D. $\sqrt{17}$
E. $3$
$y=x^2-\dfrac54x+\dfrac14$ параболын цэгээс $3x-4y-6=0$ шулуун хүртэлх хамгийн бага зайг ол.
A. $\dfrac35$
B. $\dfrac85$
C. $\dfrac75$
D. $\dfrac57$
E. $\dfrac{\sqrt{26}}5$
$A(4;5;0)$, $B(3;3;-2)$, $C(2;2;6)$ байв. $ABC$ гурвалжны $A$ оройгоос татсан биссектрисийн суурь $D$ цэгийн координатуудын нийлбэрийг ол.
A. $5$
B. $5.1$
C. $6$
D. $5.8$
E. $7$
$A(3,-2)$, $B(-1,1)$ цэгүүдийн хоорондох зайг ол.
A. $3$
B. $\sqrt{13}$
C. $4$
D. $\sqrt{17}$
E. $5$
$y=x^2-\dfrac54x+\dfrac54$ параболын цэгээс $3x-4y-6=0$ шулуун хүртэлх хамгийн бага зайг ол.
A. $\dfrac35$
B. $\dfrac85$
C. $\dfrac75$
D. $\dfrac57$
E. $\dfrac{\sqrt{26}}5$
$A(-1;-3)$, $B(1;7)$ цэгүүд өгөгдөв. $AB$ хэрчмийн дундаж цэгийн координат аль нь вэ?
A. $(0;4)$
B. $(-1;-5)$
C. $(0;2)$
D. $(1;5)$
E. $(2;10)$
$x^2-2x+y^2+6y+6=0$ муруй дээр орших цэг аль вэ?
A. $(2;-4)$
B. $(1;1)$
C. $(0;-1)$
D. $(3;-3)$
E. $(-2;1)$
$A(3;4)$, $B(-3;12)$ бол $AB=?$
A. $5$
B. $6$
C. $8$
D. $10$
E. $13$
$x^2+2x+y^2+6y-6=0$ муруй дээр орших цэг аль вэ?
A. $(2;-4)$
B. $(1;-1)$
C. $(0;-1)$
D. $(3;-3)$
E. $(-2;1)$
$(1; -3)$, $(4; 1)$, $(7; y)$, $(x; 5)$ цэгүүд дараалсан оройнууд байх параллелограммын хувьд $x+y$-ийн утга аль вэ?
A. $8$
B. $9$
C. $10$
D. $11$
E. $13$
$(-3;0)$, $(0;-4)$ хоёр цэгийн хоорондох зай аль вэ?
A. $5.2$
B. $7$
C. $6$
D. $5$
E. $3$
$x^2-2x+y^2+6y+6=0$ муруй дээр орших цэг аль вэ?
A. $(2;-4)$
B. $(1;1)$
C. $(0;-1)$
D. $(3;-3)$
E. $(-2;1)$
$MN$ хэрчмийн дундаж $K(0;2;3)$ ба $M(-2;3;1)$ бол $N$
цэгийн координат аль вэ?
A. $(1;2;5)$
B. $(2;5;1)$
C. $(5;2;1)$
D. $(2;1;5)$
$(1; -3)$, $(4; 1)$, $(7; y)$, $(x; 5)$ цэгүүд дараалсан оройнууд байх параллелограммын хувьд $x+y$-ийн утга аль вэ?
A. $8$
B. $9$
C. $10$
D. $11$
E. $13$
$ABC$ гурвалжны $A(4;3)$, $B(7;3)$, $C(9;5)$ бол $AD$ медианы уртыг ол.
A. $4$
B. $3\sqrt{2}$
C. $\sqrt{17}$
D. $3\sqrt{3}$
E. $6$
$y=x^2-6x+K$ парабол $T(3;2)$ дээр оройтой тул $K=\fbox{ab}$ байна. $A(3;1)$; $B(5;3)$ цэгүүдийг дайрсан $y=x-\fbox{c}$ тэгшитгэлтэй шулуун өгөгдөв. Парабол дээр орших $(AB)$ шулуунд хамгийн ойр цэг нь $M(\fbox{d}/2;\fbox{e}/4)$ болно. $AM$; $BM$ хэрчмүүдийн үргэлжлэлүүд нь параболыг харгалзан $F; E$ цэгүүдээр огтлох бол $\dfrac{S_{\triangle AMB}}{S_{\triangle FME}}=\fbox{f}$ байна.
$y=x^2-4x+K$ парабол $T(2;1)$ дээр оройтой тул $K=\fbox{a}$ байна. $A(2;0)$; $B(4;2)$ цэгүүдийг дайрсан $y=x-\fbox{b}$ тэгшитгэлтэй шулуун өгөгдөв. Парабол дээр орших $AB$ шулуунд хамгийн ойр цэг нь $M(\fbox{c}/2;\fbox{d}/4)$ болно. $AM; BM$ хэрчмүүдийн үргэлжлэлүүд нь параболыг харгалзан $F; E$ цэгүүдээр огтлох бол $\dfrac{S_{\triangle AMB}}{S_{\triangle FME}}=\fbox{e}$ байна.
Хавтгайд хоорондоо 6 нэгж зайтай $A$ цэг ба $m$ шулуун байв.
- Энэ цэг ба шулуунаас ижил зайд байрлах цэгүүдийн олонлог нь $y=\dfrac{x^2}{\fbox{ab}}$ функцийн график болох муруйг дүрсэлнэ.
- Энэ муруйн тэгш хэмийн тэнхлэгээс хоёр тийш 18 нэгж зайнд түүнтэй параллель байрлах $m_1$ ба $m_2$ шулуун болон $y=\dfrac{x^2}{\fbox{ab}}$ муруй, $m$ шулууны хооронд хашигдсан дүрсийн талбай нь $S=\fbox{cde}$ байна.
$x^2-6x+y^2-10y+9=0$ тойргийн $M(0;1)$ цэгт татсан шүргэгч шулуун ба түүнд татсан перпендикуляр шулууны тэгшитгэлийг бич. $(x-a)^2+(y-b)^2=r^2$ буюу тойргийн төв $A(\fbox{a};\fbox{b})$, тойргийн радиус $\fbox{c}$ болно. $AM$ шулууны тэгшитгэл нь $y=\dfrac{\fbox{d}}{\fbox{e}}x+1$ ба түүнд перпендикуляр $M(0;1)$ цэгийг дайрсан бидний олох шулууны тэгшитгэл нь $\fbox{f}x+\fbox{g}y-4=0$ болно.
Зургаас дараах функцийн
$$f(x)=\left\{\begin{array}{lll}\fbox{ab}, & x\le-2 & (2\text{ оноо)}\\ \fbox{c}\cdot x+\fbox{d}, & -2< x\le -1 & (2\text{ оноо)}\\ \fbox{e}\cdot x+\fbox{f}, & -1< x\le 0 & (2\text{ оноо)}\\ \fbox{g}, & x>0 & (1\text{ оноо)}\end{array}\right.$$

Координатын хавтгайд $A(1,2)$, $B(-1,1)$, $C(1,0)$, $D(-1,0)$ цэгүүд өгөв. $P(p,0)$ нь $CD$ хэрчим дээр орших ба $\angle APB$ өнцөг хамгийн их байхаар $P$ цэгийг олъё. $\alpha=\angle APC, \beta=\angle BPD, \theta=\angle APB$ гэвэл $\alpha+\beta+\theta=180^{\circ}$ ба $$\tg\alpha=\dfrac{\fbox{a}}{\fbox{b}-p},\tg\beta=\dfrac{\fbox{c}}{p+\fbox{d}}, \tg\theta=\dfrac{p+\fbox{e}}{p^2+\fbox{f}}$$ болно. Уламжлал авбал $(\tg\theta)'=-\dfrac{p^2+\fbox{g}p-1}{(p^2+\fbox{h})^2}$ болно. Эндээс $\theta$ өнцөг хамгийн их байх $P$ цэгийн координат $( \sqrt{\fbox{ij}}-\fbox{k},0)$ байна.
$A(1,1), B(-3,4), C(3,2)$ цэгүүд өгөв.
- $AB$ хэрчмийн урт $\fbox{a}$ байна.
- $AB$ шулууны тэгшитгэл $\fbox{b}x+\fbox{c}y-\fbox{d}=0$ байна.
- $C$ цэгээс $AB$ шулуун хүртэлх зай $\fbox{e}$ болно.
- $ABC$ гурвалжны талбай $\fbox{f}$ байна.
$A(1;1)$, $B(2;3)$, $C(4;-2)$ цэгүүд өгөгдөв. $AB$ хэрчмийн урт $\sqrt{\fbox{a}}$, $AB$ шулууны тэгшитгэл $\fbox{b}x-\fbox{c}y-1=0$ байна. $C$ цэгээс $AB$ шулуун хүртэлх зай $\dfrac{\fbox{d}}{\sqrt{\fbox{e}}}$ бөгөөд $ABC$ гурвалжны талбай нь $\dfrac{\fbox{f}}{\fbox{g}}$ байна.
$A(1;1), B(-3;4), C(3;2)$ цэгүүд өгөгдөв.
- $AB$ хэрчмийн урт $\fbox{a}$ байна.
- $AB$ шулууны тэгшитгэл $\fbox{b}x+\fbox{c}y-\fbox{d}=0$ байна.
- $C$ цэгээс $AB$ шулуун хүртэлх зай $\fbox{e}$ болно.
- $ABC$ гурвалжны талбай $\fbox{f}$ байна.
$y=\dfrac{x-2}{x-1}$ функц өгөгдөв.
- $y=\dfrac{x-2}{x-1}$ функцийн $x_0=2$ цэгт татсан шүргэгч шулууны тэгшитгэлийг бичвэл $y=\fbox{a}x-\fbox{b}$;
- $y=\dfrac{x-2}{x-1}$, $x=2$, $x=5$ ба $y=0$ шугамуудаар хүрээлэгдсэн дүрсийн талбай $\fbox{c}-\ln\fbox{d}$;
- $y=5x+5$ шулуунд перпендикулар ба $(1;1)$ цэгийг дайрсан шулууны тэгшитгэл нь $\fbox{e}x+\fbox{f}y-6=0$;
- $y=\dfrac{x-2}{x-1}$ муруй ба $x-3y-2=0$ шулууны огтлолцлын цэгүүдийн хоорондох зай $\dfrac{2}{3}\sqrt{\fbox{gh}}$.
$y=\dfrac{x}{x-1}$ функц өгөгдөв.
- $y=\dfrac{x}{x-1}$ функцийн $x_0=2$ цэгт татсан шүргэгч шулууны тэгшитгэлийг бичвэл $y=-\fbox{a}x+\fbox{b}$
- $y=\dfrac{x}{x-1}$, $x=2$, $x=4$ ба $y=0$ шугамуудаар хүрээлэгдсэн дүрсийн талбай $\fbox{c}+\ln\fbox{d}$
- $y=2x+5$ шулуунд перпендикуляр ба $(1;1)$ цэгийг дайрсан шулууны тэгшитгэл нь $\fbox{e}x+\fbox{f}y-3=0$.
- $y=\dfrac{x}{x-1}$ функц ба $x+5y-12=0$ шулууны огтлолцлын цэгүүдийн хоорондох зай $\dfrac45\sqrt{\fbox{gh}}$
Хавтгай дээр хоорондоо 6 нэгж зайтай $A$ цэг ба $m$ шулуун байв.
- Энэ цэг ба шулуунаас ижил зайд байрлах цэгүүдийн олонлог нь $y=\dfrac{x^2}{\fbox{ab}}$ функцийн график болох муруйг дүрсэлнэ. $\text{a}$ ба $\text{b}$ нь хэд вэ?
- Энэ муруйн тэгш хэмийн тэнхлэгээс хоёр тийш 18 нэгж зайд түүнтэй параллель байрлах $m_1$ ба $m_2$ шулуун болон $y=\dfrac{x^2}{\fbox{ab}}$ муруй, $m$ шулууны хооронд хашигдсан дүрсийн талбай нь $S=\fbox{cde}$ байна.
$y=\dfrac{x}{x-1}$ функц өгөгдөв.
- $y=\dfrac{x}{x-1}$ функцийн $x_0=0$ цэгт татсан шүргэгч шулууны тэгшитгэлийг бичвэл $y=-\fbox{a}x+\fbox{b}$;
- $y=\dfrac{x}{x-1}$, $x=2$, $x=5$ ба $y=0$ шугамуудаар хүрээлэгдсэн дүрсийн талбай $\fbox{c}+\ln\fbox{d}$;
- $y=3x+5$ шулуунд перпендикулар ба $(1;1)$ цэгийг дайрсан шулууны тэгшитгэл нь $\fbox{e}x+\fbox{f}y-4=0$;
- $y=\dfrac{x}{x-1}$ муруй ба $x+4y-10=0$ шулууны огтлолцлын цэгүүдийн хоорондох зай $\dfrac{3}{4}\sqrt{\fbox{gh}}$.
$y=\dfrac{x-2}{x-1}$ функц өгөгдөв.
- $y=\dfrac{x-2}{x-1}$ функцийн $x_0=0$ цэгт татсан шүргэгч шулууны тэгшитгэлийг бичвэл $y=\fbox{a}x+\fbox{b}$;
- $y=\dfrac{x-2}{x-1}$, $x=2$, $x=4$ ба $y=0$ шугамуудаар хүрээлэгдсэн дүрсийн талбай $\fbox{c}-\ln\fbox{d}$;
- $y=4x+5$ шулуунд перпендикулар ба $(1;1)$ цэгийг дайрсан шулууны тэгшитгэл нь $\fbox{e}x+\fbox{f}y-5=0$;
- $y=\dfrac{x-2}{x-1}$ муруй ба $x-3y+6=0$ шулууны огтлолцлын цэгүүдийн хоорондох зай $\dfrac23\sqrt{\fbox{gh}}$.
Зургаас дараах функцийн $a,b,c,d,e,f,g$-г ол.
$$f(x)=\left\{\begin{array}{lll}\fbox{ab}, & x\le-2 & (2\text{ оноо)}\\ \fbox{c}\cdot x+\fbox{d}, & -2< x\le -1 & (2\text{ оноо)}\\ \fbox{e}\cdot x+\fbox{f}, & -1< x\le 0 & (2\text{ оноо)}\\ \fbox{g}, & x>0 & (1\text{ оноо)}\end{array}\right.$$
$$f(x)=\left\{\begin{array}{lll}\fbox{ab}, & x\le-2 & (2\text{ оноо)}\\ \fbox{c}\cdot x+\fbox{d}, & -2< x\le -1 & (2\text{ оноо)}\\ \fbox{e}\cdot x+\fbox{f}, & -1< x\le 0 & (2\text{ оноо)}\\ \fbox{g}, & x>0 & (1\text{ оноо)}\end{array}\right.$$

$A(2;3)$, $B(-2;0)$ бол $AB$ шулууны тэгшитгэл $\fbox{a}x-\fbox{b}y+\fbox{c}=0$ координатын эхээс $AB$ шулуун хүртэлх хамгийн богино зай $d=\dfrac{\fbox{d}}{\fbox{e}}$ байна.
Координатын систем
$A(2,-1)$, $P(-1,1)$ цэгүүд өгөгдөв. $A$ төвтэй төвийн тэгш хэмээр $P$ цэг $Q$-д буусан бол $Q$ цэгийн координат $(p,q)$-г ол.
Координатын хавтгайд $A(1,2)$, $B(5,4)$, $C(3,6)$, $D(x,y)$ цэгүүд өгөгдөв.
- Эдгээр цэгүүд параллелограммын дөрвөн орой үүсгэх $D$ цэгийн координатыг ол.
- $AD^2+BD^2+CD^2$ хамгийн бага байх $D$ цэгийн координатыг ол.
$x^2+y^2=4 \boldsymbol{\cdots}(1)$, $x^2+y^2-8x-4y+4=0 \boldsymbol{\cdots}(2)$ тойргуудын хувьд дараах acуултанд хариул.
- Хоёр тойрог огтлолцох эсэхийг шинжил.
- Хоёр тойргийн огтлолцлын цэгийн координатыг ол.
$(x-a\cos\theta)^2+(y-a\sin \theta)^2=1$ ($a$ нь $0< a< 1$ тогтмол
тоо) тойрог $OX$ тэнхлэгийг $A$ ба $C$, $OY$-тэнхлэгийг $B, D$
цэгүүдээр огтлох ба $A$ цэгийн абсцисс, $B$-ийн ординат эерэг.
- $ABCD$ дөрвөн өнцөгтийн талбайг $a$ ба $\theta$-өөр илэрхийл.
- $\theta$ нь $0^{\circ}< \theta< 90^{\circ}$ мужаар хөдөлж байх үед $S_{ABCD}$-ийн хамгийн их утгыг ол. $\max (S_{ABCD})$ үеийн $\theta$-ийн утгыг ол.
Дараах нөхцлийг хангах шулууны тэгшитгэлийг бич.
- $(-1,3)$ цэгийг дайрсан $-2$ өнцгийн коэффициенттэй;
- $(1,-2)$ ба $(-3,4)$ цэгүүдийг дайрсан;
- $(4,1)$ ба $(4,5)$ цэгүүдийг дайрсан;
- $(3,-2)$ цэгийг дайрсан $4x-5y+3=0$ шулуунтай параллель;
- $P(-1,2)$, $Q(1,-3)$ цэгүүд өгөгдөв. $PQ$-ийн дундаж цэгийг дайрсан $PQ$-д перпендикуляр шулуун.
Координатын шулуун дээр $A(-2)$, $B(1)$, $C(5)$ цэгүүд өгөгдөв.
- $AB$, $CA$ хэрчмүүдийн уртыг ол.
- $AB$ хэрчмийг $3:2$ харьцаагаар хуваах $P$, $3:2$ харьцаагаар гадаад байдлаар хуваах $Q$, $2:3$ харьцаагаар гадаад байдлаар хуваах $R$ цэгүүдийг ол.
Гурвалжны гурван өндөр нэг цэгт огтлолцохыг батал.
$O(0, 0)$ ба $O$-г дайрсан
шулуун дээр $O$-ийн нэг талд орших $P(x, y)$, $Q(X, Y)$ цэгүүдийн
хувьд $OP\cdot OQ=2$ байв.
- $x, y$-ийг $X, Y$-ээр илэрхийл.
- $P$ цэг $x+2y=1$ шулуунаар хөдлөхөд $Q$ цэгийн геометр байрыг ол.
$A(6, 0)$, $B(3, 3)$, $P$ цэг $x^2+y^2=9$ тойргоор хөдлөхөд $ABP$ гурвалжны хүндийн төв $G$ ямар дүрс зурах вэ?
$A(5,4), B(0,-1), C(8,-2)$ цэгүүд өгөгдөв.
- $AB$ хэрчмийг дотоод байдлаар $3:2$ харьцаагаар хуваах $P$ цэг, $3:2$ харьцаагаар гадаад байдлаар хуваах $Q$ цэгүүдийг ол.
- $\triangle ABC$-ийн хүндийн төв $G$ цэгийг ол.
- $\triangle PQR$-ийн хүндийн төв $G$ бол $R$ цэгийг ол.
$y=x^2$ параболыг $y=mx+2-m$ шулуун $A, B$ гэсэн ялгаатай цэгүүдээр огтлохыг харуул. $m$ хувьсах үед $AB$ хөвчийн дундаж цэг $P$-ийн геометр байрыг ол.
$P: y=x^2+kx+1, A(2,1), B(4,7)$ гэе.
- $A, B$ цэгүүд $P$ муруйгаар таслагдсан хавтгайн өөр өөр хэсгүүдэд байх $k$-г ол.
- $AB$ хэрчим $P$ муруйтэй ерөнхий цэгтэй байх $k$-г ол.
Координатын хавтгайд $O(0, 0)$ , $A(1, 3)$, $B(5, 6)$, $C(-2, 7)$, $D(t, 0) [t>0]$ цэгүүд өгөгдөв.
- $O$ ба $A$, $A$ ба $B$ цэгүүдийн хоорондын зайг ол.
- $\triangle ABC $ тэгш өнцөгт гэдгийг харуул.
- $\triangle ABD$ нь адил хажуут байх $t$-г ол.
$a$ нь $0< a< 1$ байх бодит тоо.
$x, y$ нь $a^6\leq x^2y^3\leq a^3, 0< x\leq 1, 0< y\leq 1$ нөхцлийг
хангах бол $F=(\log_ax)^2+(\log_ay)^2$ илэрхийллийн хамгийн их ба
хамгийн бага утгыг ол.
Дараах мужид $r$-ийн хамгийн бага утга, $q$-ийн хамгийн их ба бага утгуудыг ол.
- $x-y\geq 0$, $x+2y\geq 6$ бол $r=x^2+y^2;$
- $|x+y|\leq1$, $|2x-y|\leq 1$ бол $q=2x-y-(x+y)^2.$
$3x^2-2xy-y^2+ax+6y-8=0$ тэгшитгэлээр илэрхийлэгдэх муруй хоёр шулууныг дүрслэх бол $a$-г олж, шулуунуудын тэгшитгэлийг бич.
$A(3, 5)$, $B(5, 2)$, $C(1, 1)$ цэгүүдээр тодорхойлогдох $\triangle ABC$ гурвалжны талбайг ол.
$y=x^2 \boldsymbol{\cdots}(1)$ парабол ба $x^2+(y-2)^2=r^2, (r>0) \boldsymbol{\cdots}(2)$ тойрог өгөгдөв.
- Дөрвөн цэгээр огтлолцох $r$-ийн утгын мужийг ол.
- Тойрог ба парабол шүргэлцэх $r$-ийн утгыг ол.
$\triangle ABC$-ийн $BC$ талын дундаж нь $M$ цэг бол $$AB^2+AC^2=2(AM^2+BM^2)$$ гэж батал.
$y=-x^2+4$, $y=x^2-2x$ параболуудыг $C_1$, $C_2$ гэе. $C_1$,
$C_2$-оор хашигдсан дүрсийг $G$ гэе.
- $G$ нь ямар нэгэн $P$ цэгийн хувьд тэгш хэмтэй гэдгийг харуул. Өөрөөр хэлбэл $Q$ нь $G$-ээр хөдөлж байх үед ямар нэгэн $P$ цэгийн хувьд $Q$ цэгийн тэгш хэмтэй $Q^\prime\in G$ байна.
- $(x, y)\in G$ үед $(y+x-2)^2$ илэрхийллийн хамгийн их утгыг ол.
$xy$ хавтгайд $y\geq x^2$ тэнцэтгэл бишээр илэрхийлэгдэх
мужийг $D$ гэе. $D$-д агуулагдах нэг талын урт нь $t$ ба нэг тал
нь $x$ тэнхлэгтэй параллель байх бүх зөв гурвалжнуудыг авч үзье.
Эдгээр гурвалжны хүндийн төвийн $y$ координатын хамгийн бага утгыг
$t$-ээс хамааруулан бич.
$a\geq 0$ бодит тоо. $x\geq 0$, $y\geq 0$, $y\leq
-x^2+x+a$-аар илэрхийлэгдэх мужид агуулагдах, нэг тал нь $x$
тэнхлэг дээр байрлах квадратууд дотроос хамгийн их талтай квадратын
талыг $a$-аар илэрхийл.
$xy$ хавтгайд $C\colon x^2+y^2=1$-ын гадна орших $P(a,b)$ цэг
байв. $P$-ээс $C$ тойрогт татсан хоёр шүргэгчийн шүргэх цэгийг
$Q_1$, $Q_2$ гэе. $Q_1$, $Q_2$ хэрчмийн дундаж цэгийг $Q$ гэе. $P$
цэг нь $C$ дээр оршихгүй бөгөөд $x(x-y+1)< 0$ хангах мужаар гүйх
үед $Q$-ийн геометр байрыг олж зур.
$xy$ хавтгайд $P(a, b)$ цэгийн хувьд $|x-a|\leq \dfrac12$,
$|y-b|\leq \dfrac12$-ыг $S(P)$ гэе. Координатын эх болон $S(P)$-ын
хоорондох хамгийн бага зайг $f(P)$ гэе. $(2,1)$ төвтэй 1 радиустай
тойрог дээр $P$ цэг хөдлөх үед $f(P)$-ийн хамгийн их утгыг ол.
$\angle AOB=2\theta$ ба энэ өнцгийн биссектрис $OC$ байг. $OC$ хэрчим дээр $OM=2$ байх $M$ цэг авъя. $M$ цэгийг дайрсан
шулууны $OA$, $OB$-тэй огтлолцох цэгүүдийг харгалзан $X$, $Y$ гэе. $OX$-ийн уртыг $x$, $OY$-ийн уртыг $y$ гэвэл
- $\dfrac 1x+\dfrac 1y$-ийг $\theta$-өөр илэрхийл.
- $x^2+y^2$-ийн хамгийн бага утгыг ол.
Өгөгдсөн $A(1,0)$ цэг ба координатын эх дээр төвтэй, 1
радиустай тойргийн дурын $P$ цэгийн хувьд $PA^2+PB^2+PC^2$ нь $P$
цэгийн байрлалаас үл хамаарах тогтмол тоо бол
- $B$, $C$-ийн координатыг ол.
- $PA+PB+PC$ нийлбэрийн хамгийн их ба хамгийн бага утгыг ол.
- $PA\cdot PB\cdot PC$-үржвэрийг $\sin\alpha$-аар илэрхийл, $\alpha=\measuredangle PAB.$
$ABCD$ параллелограммын хувьд $\overrightarrow{AC}=\vec{\mathstrut{p}}$,
$\overrightarrow{BD}=\vec{\mathstrut{q}}$ бол $\overrightarrow{AB}$, $\overrightarrow{AD}$
векторуудыг $\vec{\mathstrut{p}}$, $\vec{\mathstrut{q}}$-ээр
илэрхийл.
$\triangle ABC$-ийн $BC$, $CA$, $AB$ талуудыг ижил харьцаагаар хуваах цэгүүдийг харгалзан $L$, $M$, $N$ гэе. $\triangle LMN$-ийн хүндийн төв нь $\triangle ABC$-ийн хүндийн төвтэй давхцахыг харуул.
$P(1,2)$ цэг ба $\ell\colon 3x+4y-15=0$, $m\colon x+2y-5=0$ шулуунууд өгөгдөв.
- $\ell$ шулууны хувьд $P$-тэй тэгш хэмтэй $Q$ цэгийн координатыг ол.
- $\ell$ шулууны хувьд $m$-тэй тэгш хэмтэй шулууныг ол.
$A(-4,0)$ ба $B(2,0)$ цэгүүд хүртэлх зайнуудынх нь харьцаа $2:1$ байх цэгүүдийн геометр байрыг ол.
$ABC$ гурвалжны $BC$ талын дундаж $M$ бол $AB^2+AC^2=2(AM^2+BM^2)$ болохыг батал.
$a$, $b$, $x$, $y$ бодит тоонууд $a^2+b^2=2$, $x^2+y^2=3$ нөхцлүүдийг хангах
үед $ax+by$-ийн хамгийн их ба хамгийн бага утгуудыг ол.
$y=x^2$ парабол, $\ell\colon y=k$ шулуун өгөгдөв.
- Параболын $(a, a^2)$ цэг дээрх нормаль шулуун $\ell$ шулууныг $P$ цэгт огтолно. $P$ цэгийн абсциссийг $b$ гэвэл $b$-г $a, k$-аар илэрхийл.
- $\ell$ шулуун дээрх $P(b, k)$ цэгийг параболын гурван өөр нормал шулуун дайрдаг байх $b$-ийн утгын мужийг ол.
$xy$ координатын хавтгайн эх $O$ дээр төвтэй нэгж радиустай тойрог дээр $P(\cos\theta, \sin \theta)$, $Q(\cos2 \theta, \sin2\theta)$ цэгүүд авав. $(0^{\circ}< \theta< 45^{\circ})$ $P$-ээс $x$ тэнхлэг рүү буулгасан перпендикулярийн суурийг $M$ гэе. $M$ төвтэй $MP$ радиустай
тойргийн $x$ тэнхлэгтэй огтлолцох цэгүүдийн $O$-тэй ойрхон нь $R$ байв.
- $t=\cos \theta-\sin\theta$ гэвэл $t$-ийн утгын мужийг ол.
- $\triangle OQR$-ийн талбай $S$-ийг $t$-ээр илэрхийл.
- $S$-ийн хамгийн их утгыг ол.
$O$-координатын төв $(a\geq 0)$ байг. $A(a, 0)$ төвтэй, 1 радиустай торгийг $C$ гэе. $C$ тойрог ба $x$ тэнхлэгийн огтлолын цэгийн баруун талынхыг нь $B$ гэе. $0^{\circ}\leq \theta\leq 45^{\circ}$ үед $C$-ийн I мөч дахь $PQ$ хоёр цэгийн хувьд $\angle PAB=\theta$, $\angle QAB=2\theta$ байг. $P$ цэгээс $y$ тэнхлэг рүү буулгасан перпендикулярийн суурийг $P^\prime $, $Q$ цэгээс $x$ тэнхлэг рүү буулгасан перпендикулярийн суурийг $Q^\prime $ гэе. $OP$, $OQ$-талтай тэгш өнцөгтийн талбай $S$-н хувьд
- $t=\sin \theta$ гэвэл $S$-ийг $a, t$-р илэрхийл.
- $\theta$ нь $0^{\circ}< \theta\leq 45^{\circ}$ мужид хувьсах үед $S$-ийн хамгийн их утга болон тэр үеийн $t$-ийн утгыг $a$-р илэрхийл.
$2x^2-5xy+2y^2+5x+ay+2=0$ тэгшитгэл хоёр шулууныг дүрслэх
бол $a$-г олж, шулуунуудын тэгшитгэлийг бич.
Дараах нөхцлийг хангах $P$-цэгийн геометр байрыг ол.
- $A(3, 6)$, $B(-6, 0)$, $C(6, 0)$ ба $AP^2+BP^2+CP^2=150.$
- $A(0, 0)$, $B(2, 0)$, $C(0, 2)$ ба $2AP^2=BP^2+CP^2.$
$A(2,3)$, $B(6,1)$ цэгүүдээс ижил зайд орших $P$ цэгийн геометр байрыг ол. Мөн $A$ ба $B$ хүртэлх зайнуудын харьцаа $1:3$ байх $Q$ цэгийн геометр байрыг ол.
$Q$ цэг $F$ муруй дээгүүр хөдлөхөд $P$ цэгийн геометр байрыг ол. $O$ координатын эх.
- $F: 3x+2y=22$ үед $OQ$ хэрчмийн дундаж $P$ цэг;
- $F: 3x+2y=22$ $(2\leq x\leq 6)$ үед $OQ$ хэрчмийн дундаж $P$ цэг;
- $F: x^2+y^2-8x-12y+32=0$ үед $OQ$ хэрчмийг 1:3 харьцаанд хуваах $P$ цэг.
$P$ цэг $y=x^2$ муруйгаар хөдлөхөд $Q$, $R$ цэгүүдийн геометр байрыг ол. Энд $A(1, 2)$, $B(-1,-2)$, $C(4,-1).$
- $AP$ хэрчмийг 2:1 дотоод харьцаанд хуваах $Q$ цэг;
- $\triangle PBC$-ны хүндийн төв $R$.
Дараах муруй ба шулууны огтлолцох нөхцлийг тогтоож
огтлолцлын цэгүүдийн дундаж цэгийн геометр байрыг ол.
- $y=x^2$ ба $y=m(x-2)$
- $(x-1)^2+y^2=4$ тойрог ба координатын эхийг дайрсан шулуун.
Дараах нөхцлийг хангах мужуудыг $xy$ хавтгайд дүрсэл.
- $2x-3y-6< 0$
- $3x+2>0$
- $y>x^2-2x$
- $y\leq 4x-x^2$
- $(x-1)^2+(y-2)^2< 9$
- $x^2+y>0$, $x+y+2>0$
- $x^2+y^2\geq 4$, $x+2y+2< 0$
- []
Дараах нөхцөл хангасан цэгүүдийн олонлогийг дүрсэл.
- $(y-x)(x+y-2)>0$
- $(y-x^2)(x-y+2)\geq 0$
- $(x^2-y^2)(2x+y-1)< 0$
- $xy(x^2+y^2-1)>0$
Дараах нөхцөл хангасан цэгүүдийн олонлогийг дүрсэл.
- $|x+y|>2$
- $|x|+|y|< 1$
- $|x-1|+|y-2|\leq 1$
Нэгэн компани $A$ бүтээгдэхүүнийг хийхэд 2 кВт цахилгаан, 2 м.куб газ, 3 кг материал ашигладаг ба $B$ бүтээгдэхүүнийг хийхэд 3 кВт цахилгаан, 1 м.куб газ, 3 кг материал тус, тус ашигладаг. Тэгвэл 19 кВт цахилгаан, 13 м.куб газ, 18 кг $A$-ын материал, 15 кг $B$-ын материал ашиглан 10000 төгрөгийн үнэтэй $A$ бүтээгдэхүүн, 50000 төгрөгийн үнэтэй $B$ бүтээгдэхүүн тус тус хэчнээнийг хийвэл хамгийн их орлого олох вэ?
Нэгэн зоогийн газар өөрт байгаа 460 гр мах, 390 гр сонгино ашиглан котлет, бөөрөнхий мах хийнэ. 1 котлет хийхэд 50 гр мах, 25 гр
сонгино, 1 бөөрөнхий мах хийхэд 20 гр мах, 30 гр сонгино шаардлагатай. Котлет 400 төгрөг, бөөрөнхий мах 300 төгрөг бол хамгийн их орлого олохын
тулд тус бүр хэчнээнийг хийх вэ? Үүнд бусад материалыг хангалттай байгаа гэж үзнэ.
$P, Q$-ийн хамгийн их, хамгийн бага утгуудыг ол.
- $x\geq 0$, $y\geq 0$, $2x+3y\leq 6$ үед $P=x+y;$
- $x\geq 0$, $y\geq 0$, $x+2y\leq 6$, $2x+y\leq 6$ үед $P=x-y;$
- $x+y\geq 1$, $2x+y\leq 6$, $x+2y\leq 4$ үед $P=2x+3y$, $Q=2x+y.$
$x, y$ нь дараах нөхцлийг хангах үед $P$-ийн хамгийн их ба бага утгуудыг ол.
- $x^2+y^2\leq 5$ үед $P=x+2y;$
- $x^2+y^2\leq 1$, $y\geq 0$ үед $P=x+y;$
- $x^2+y^2\leq 4$, $x\leq 0$ үед $P=3x-4y.$
- $|x^2-1|+|y-1|\leq 1$ нөхцлийг хангах мужийг $xy$ хавтгайд дүрсэлж,
- $p=y-x$-ийн хамгийн их, бага утга,
- $q=x^2+y^2$-ийн хамгийн бага утгыг ол.
- $(x-2)^2+(y+1)^2\leq 4$ үед $|x|+|y|$ илэрхийлэл хамгийн их, хамгийн бага утгаа авах $(x, y)$-ийг ол.
$y=x^2-2x+a$ муруйн хоёр өөр мужид $(3, 1)$, $(4, 2)$
цэгүүд оршдог бол $a$-г ол.
$A(1, 3)$, $B(4, 1)$ байг. $AB$ хэрчим $x^2+y^2=ax$ тойрогтой
нэг ерөнхий цэгтэй байх $a$-ийн утгыг ол.
$A(3, 1)$ ба $B(4, 2)$ цэгүүд $y=x^2-2x+a$ параболаар хуваагдах
хавтгайн өөр, өөр хэсгүүдэд байх $a$ параметрийн утгыг ол.
$x^2+(y-t)^2=4t-2$ тойрог $P(t, a)$ цэг.
- $t=1$ үед $P$ цэг тойргийн гадна оршиж байх $a$-г ол;
- $2< t< 3$ үед $P$ цэг тойргийн дотор оршиж байх $a$-г ол.
$(x-t)^2+(y-t)^2=t^2+1$ тойрогууд ба $P(a, a)$ цэг өгөгдөв.
$P$ цэг $t=1$-д харгалзах тойргийн дотор, $t=2$-д харгалзах
тойргийн гадна орших $a$ параметрийн утгуудыг ол.
$\angle XOY$-өнцгийн дотор орших тогтмол
$M$ цэгийг дайрах шулуун $OX$ ба $OY$-ийг огтлох цэгийг харгалзан
$P$, $Q$ гэе. $|OM|=2$, $\angle POM=15^{\circ}$, $\angle
QOM=45^{\circ}$, $\angle OMQ=\theta$ гээд $f(\theta)=\dfrac 1{MP}+\dfrac
1{MQ}$ гэвэл $f(\theta)$-ийн утгын мужийг ол.
$y=x^2$
параболын $A, B$ цэгүүд дээрх шүргэгч шулуунуудын огтлолын цэгийг
$P$ гэе. Эдгээр 2 шулуун ба параболоор зааглагдсан дүрсийн талбай
$S$ нь тогтмол 2 байхаар $A, B$ цэгүүд хөдлөхөд $P$ цэгийн геометр
байрыг ол.
$(1; -3)$, $(4; 1)$, $(7; y)$, $(x; 5)$ цэгүүд дараалсан оройнууд байх параллелограммын хувьд $x+y$-ийн утга аль вэ?
A. $8$
B. $9$
C. $10$
D. $11$
E. $13$
$7$ см талтай $ABCD$ квадратын $AD$ талын дундаж цэг $K$ болно. $CK$ шулууны дагуу цаасыг нугалж тэр хоёр талст өнцгийг $60^\circ$ болгов. $B$ ба $D$ цэгүүдийн хоорондох зайг ол.
A. $14\sqrt{5}$
B. $7\sqrt5$
C. $\frac{14\sqrt5}{5}$
D. $\frac{7\sqrt5}{5}$
E. $\frac{2\sqrt5}{5}$
$A(-2,4,6)$; $B(6,2,4)$; $C(1,-1,-3)$ цэгүүдэд оройтой $ABC$ гурвалжны $C$ оройгоос татсан медианы уртыг ол.
A. 4
B. 6
C. 8
D. 9
E. 10
Координатын хавтгайд $A(-1,1)$ ба $B(3,4)$ цэгүүд өгөв. $O(0,0)$ цэгээс $AB$ шулуун хүрэх хамгийн богино зайг ол.
A. $\dfrac85$
B. $1.4$
C. $\sqrt3$
D. $0.8$
E. $\sqrt2$
$A(1;3)$, $B(5;3)$, $C(1;6)$ бол $ABC$ тэгш өнцөгт гурвалжны гипотенузын дундаж цэгийг ол.
A. $(6;9)$
B. $(1;4.5)$
C. $(3;4.5)$
D. $\big(\frac{7}{3};4\big)$
E. $(3;3)$
$ABC$ гурвалжны $A(3;4)$, $B(3;7)$, $C(5;9)$ бол $AD$ медианы уртыг ол.
A. $4$
B. $\sqrt{17}$
C. $3\sqrt{2}$
D. $3\sqrt{3}$
E. $5$
$y=x^2$ парабол $y=2x-a$ шулуунтай огтлолцохгүй байх $a$ тооны мужийг ол.
A. $a<-1$
B. $a>-1$
C. $a<1$
D. $a>1$
E. $-1< a<1$
$OM=\sqrt2$, $ON=\sqrt8$, $MN=3\sqrt2$ бол аль цэг нөгөө
хоёрынхоо хооронд орших вэ?
A. $M$
B. $N$
C. $O$
D. аль нь ч биш
E. аль нь ч байж болно
$PQ=\sqrt3$, $QR=3\sqrt3$, $PR=\sqrt{12}$ байх гурван цэгийн
аль нь нөгөө хоёрын хооронд орших вэ?
A. $P$
B. $Q$
C. $R$
D. аль нь ч биш
E. аль нь ч байж болно
$(1;0)$, $(0;-3)$, $(0;3)$ цэгт оройтой гурвалжин ямар гурвалжин бэ?
A. адил хажуут
B. тэнцүү талт
C. элдэв талт
D. тэгш өнцөгт
E. аль нь ч биш
$(-7;0)$, $(0;-3)$, $(0;3)$ цэгийг холбоход ямар гурвалжин үүсэх бэ?
A. элдэв талт
B. тэнцүү талт
C. адил хажуут
D. тэгш өнцөгт
E. аль нь ч биш
$(3;0)$, $(0;-4)$ гэсэн 2 цэгийн хоорондох зай хэдэн нэгж
вэ?
A. $7$
B. $6.1$
C. $5$
D. $5.2$
E. $4.5$
$(-3;0)$, $(0;-4)$ хоёр цэгийн хоорондох зай аль вэ?
A. $5.2$
B. $7$
C. $6$
D. $5$
E. $3$
$M(-2;0)$, $N(7;0)$, $L(2;4)$. $MNL$ гурвалжны $ML$ суурьтай
параллель дундаж шугамын урт аль вэ?
A. $3$
B. $2\sqrt3$
C. $2\sqrt2$
D. $\sqrt5$
E. $3\sqrt{2}$
$L(2;4)$, $N(4;0)$, $M(-2;0)$. $LNM$ гурвалжны $LN$ суурьтай
параллель дундаж шугамын урт аль вэ?
A. $\sqrt3$
B. $5$
C. $3$
D. $\sqrt5$
E. $2$
$M_1(2;0;0)$, $M_2(0;2;0)$, $M_3(0;0;3)$. $M_1M_2M_3$
гурвалжны периметр аль вэ?
A. $\sqrt2+\sqrt3$
B. $\sqrt{15}$
C. $2(\sqrt{13}+\sqrt2)$
D. $2(\sqrt2+\sqrt{11})$
E. $7$
$M_1(1;0;0)$, $M_2(0;1;0)$, $M_3(0;0;2)$. $M_1M_2M_3$
гурвалжны периметр аль вэ?
A. $2+\sqrt{10}$
B. $\sqrt2(1+\sqrt{10})$
C. $\sqrt2(1+\sqrt5)$
D. $\sqrt2+\sqrt5$
E. $4$
$M(2,-1,-3)$ цэгтэй $xOy$ хавтгайн хувьд тэгш хэмтэй цэг аль вэ?
A. $(-2,-1,3)$
B. $(2,1,3)$
C. $(2,-1,3)$
D. $(-2,1,3)$
E. $(-2,1,-3)$
$M(2;-1;3)$ цэгтэй $xOz$ хавтгайн хувьд тэгш хэмтэй цэг аль
вэ?
A. $(2;-1;-3)$
B. $(2;1;3)$
C. $(2;1;-3)$
D. $(-2;1;3)$
$M(1;2;3)$, $N(3;4;-1)$. $MN$ хэрчмийн дундаж цэг аль вэ?
A. $(-2;3;1)$
B. $B(1;1;-2)$
C. $(2;3;1)$
D. $D(0;0;1)$
$MN$ хэрчмийн дундаж $K(0;2;3)$ ба $M(-2;3;1)$ бол $N$
цэгийн координат аль вэ?
A. $(1;2;5)$
B. $(2;5;1)$
C. $(5;2;1)$
D. $(2;1;5)$
$P(2;-1;3)$ цэгтэй $Oz$ тэнхлэгийн хувьд тэгш хэмтэй цэг аль
вэ?
A. $(2;-1;3)$
B. $(-2;1;3)$
C. $(2;1;3)$
D. $(2;-1;-3)$
$P(-2;1;3)$ цэгтэй $Oz$ тэнхлэгийн хувьд тэгш хэмтэй цэг аль
вэ?
A. $(2;1;3)$
B. $(-2;-1;3)$
C. $(2;-1;3)$
D. $D(2;1;-3)$
$P(4;3;-2)$ цэгээс $Oz$ тэнхлэг хүртэлх зай аль вэ?
A. $4$
B. $3$
C. $2$
D. $5$
$P(2;-3;4)$ цэгээс $Ox$ (абсцисс) тэнхлэг хүртэлх зай аль
вэ?
A. $5$
B. $3$
C. $4$
D. $2$
E. $2\sqrt{3}$
$P(3;4;2\sqrt6)$ цэгээс координатын эх хүртэлх зай аль вэ?
A. $6$
B. $5$
C. $7$
D. $8$
$P(4;\sqrt{23};5)$ цэгээс координатын эх хүртэлх зай аль вэ?
A. $7$
B. $8$
C. $9$
D. $6$
$A(3;3)$, $B(4;6)$, $C(13;3)$ цэгүүд дээр оройтой гурвалжны $B$ оройгоос татсан медианы уртыг ол.
A. $4$
B. $5$
C. $25$
D. $2\sqrt6$
E. $4.5$
$A(2;-3;-5)$, $B(-1;5;2)$, $C(3;-3;4)$ цэгүүдэд оройтой $ABC$ гурвалжны $A$ оройгоос татсан медианы уртыг ол
A. 4
B. 6
C. 8
D. 9
E. 10
$A(0;2)$, $B(1;5)$, $C(10;2)$ цэгүүд дээр оройтой гурвалжны $B$ оройгоос татсан медианы уртыг ол.
A. $4.5$
B. $4$
C. $25$
D. $2\sqrt6$
E. $5$
$A(4,3)$, $B(-3,5)$, $C(0,-3)$ бол $\triangle ABC$-ийн талбайг ол.
A. 25
B. 26
C. 28
D. 30
E. 31
$ABC$ гурвалжны $A(-3;4)$ ба $B(1;6)$ бол $AC$ болон $CB$ талуудын дунджийг холбосон хэрчмийн уртыг олоорой.
A. $\sqrt5$
B. $3\sqrt2$
C. $2\sqrt3$
D. $2\sqrt2$
E. $2$
$A(5,4)$, $B(2,2)$, $C(-4,6)$ бол $ABC$ гурвалжны $AM$ медианы уртыг ол.
A. 2
B. 5
C. 6
D. 8
E. 10
$A(1,2)$, $B(5,-1)$ цэгүүдийн хоорондох зайг ол.
A. $5$
B. $25$
C. $\sqrt{31}$
D. $\sqrt{17}$
E. $3$
$y=x^2-\dfrac54x+\dfrac14$ параболын цэгээс $3x-4y-6=0$ шулуун хүртэлх хамгийн бага зайг ол.
A. $\dfrac35$
B. $\dfrac85$
C. $\dfrac75$
D. $\dfrac57$
E. $\dfrac{\sqrt{26}}5$
$A(4;5;0)$, $B(3;3;-2)$, $C(2;2;6)$ байв. $ABC$ гурвалжны $A$ оройгоос татсан биссектрисийн суурь $D$ цэгийн координатуудын нийлбэрийг ол.
A. $5$
B. $5.1$
C. $6$
D. $5.8$
E. $7$
$A(3,-2)$, $B(-1,1)$ цэгүүдийн хоорондох зайг ол.
A. $3$
B. $\sqrt{13}$
C. $4$
D. $\sqrt{17}$
E. $5$
$y=x^2-\dfrac54x+\dfrac54$ параболын цэгээс $3x-4y-6=0$ шулуун хүртэлх хамгийн бага зайг ол.
A. $\dfrac35$
B. $\dfrac85$
C. $\dfrac75$
D. $\dfrac57$
E. $\dfrac{\sqrt{26}}5$
$A(-1;-3)$, $B(1;7)$ цэгүүд өгөгдөв. $AB$ хэрчмийн дундаж цэгийн координат аль нь вэ?
A. $(0;4)$
B. $(-1;-5)$
C. $(0;2)$
D. $(1;5)$
E. $(2;10)$
$x^2-2x+y^2+6y+6=0$ муруй дээр орших цэг аль вэ?
A. $(2;-4)$
B. $(1;1)$
C. $(0;-1)$
D. $(3;-3)$
E. $(-2;1)$
$A(3;4)$, $B(-3;12)$ бол $AB=?$
A. $5$
B. $6$
C. $8$
D. $10$
E. $13$
$x^2+2x+y^2+6y-6=0$ муруй дээр орших цэг аль вэ?
A. $(2;-4)$
B. $(1;-1)$
C. $(0;-1)$
D. $(3;-3)$
E. $(-2;1)$
$(1; -3)$, $(4; 1)$, $(7; y)$, $(x; 5)$ цэгүүд дараалсан оройнууд байх параллелограммын хувьд $x+y$-ийн утга аль вэ?
A. $8$
B. $9$
C. $10$
D. $11$
E. $13$
$(-3;0)$, $(0;-4)$ хоёр цэгийн хоорондох зай аль вэ?
A. $5.2$
B. $7$
C. $6$
D. $5$
E. $3$
$x^2-2x+y^2+6y+6=0$ муруй дээр орших цэг аль вэ?
A. $(2;-4)$
B. $(1;1)$
C. $(0;-1)$
D. $(3;-3)$
E. $(-2;1)$
$ABC$ гурвалжны талбайг олоорой. $C(0;-2.5)$ координаттай.

A. $12.5$
B. $24.5$
C. $6.25$
D. $12.25$
E. $\dfrac{25}{2}$
$MN$ хэрчмийн дундаж $K(0;2;3)$ ба $M(-2;3;1)$ бол $N$
цэгийн координат аль вэ?
A. $(1;2;5)$
B. $(2;5;1)$
C. $(5;2;1)$
D. $(2;1;5)$
$(1; -3)$, $(4; 1)$, $(7; y)$, $(x; 5)$ цэгүүд дараалсан оройнууд байх параллелограммын хувьд $x+y$-ийн утга аль вэ?
A. $8$
B. $9$
C. $10$
D. $11$
E. $13$
$ABC$ гурвалжны $A(4;3)$, $B(7;3)$, $C(9;5)$ бол $AD$ медианы уртыг ол.
A. $4$
B. $3\sqrt{2}$
C. $\sqrt{17}$
D. $3\sqrt{3}$
E. $6$
$P(3;-2)$ цэгийг $OX$ тэнхлэгийн хувьд тэгш хэмтэй хувиргахад ямар цэг гарах вэ?
A. $(-3;2)$
B. $(-2;-3)$
C. $(-3;-2)$
D. $(-2;3)$
E. $(3;2)$
$y=x^2-6x+K$ парабол $T(3;2)$ дээр оройтой тул $K=\fbox{ab}$ байна. $A(3;1)$; $B(5;3)$ цэгүүдийг дайрсан $y=x-\fbox{c}$ тэгшитгэлтэй шулуун өгөгдөв. Парабол дээр орших $(AB)$ шулуунд хамгийн ойр цэг нь $M(\fbox{d}/2;\fbox{e}/4)$ болно. $AM$; $BM$ хэрчмүүдийн үргэлжлэлүүд нь параболыг харгалзан $F; E$ цэгүүдээр огтлох бол $\dfrac{S_{\triangle AMB}}{S_{\triangle FME}}=\fbox{f}$ байна.
$y=x^2-4x+K$ парабол $T(2;1)$ дээр оройтой тул $K=\fbox{a}$ байна. $A(2;0)$; $B(4;2)$ цэгүүдийг дайрсан $y=x-\fbox{b}$ тэгшитгэлтэй шулуун өгөгдөв. Парабол дээр орших $AB$ шулуунд хамгийн ойр цэг нь $M(\fbox{c}/2;\fbox{d}/4)$ болно. $AM; BM$ хэрчмүүдийн үргэлжлэлүүд нь параболыг харгалзан $F; E$ цэгүүдээр огтлох бол $\dfrac{S_{\triangle AMB}}{S_{\triangle FME}}=\fbox{e}$ байна.
Хавтгайд хоорондоо 6 нэгж зайтай $A$ цэг ба $m$ шулуун байв.
- Энэ цэг ба шулуунаас ижил зайд байрлах цэгүүдийн олонлог нь $y=\dfrac{x^2}{\fbox{ab}}$ функцийн график болох муруйг дүрсэлнэ.
- Энэ муруйн тэгш хэмийн тэнхлэгээс хоёр тийш 18 нэгж зайнд түүнтэй параллель байрлах $m_1$ ба $m_2$ шулуун болон $y=\dfrac{x^2}{\fbox{ab}}$ муруй, $m$ шулууны хооронд хашигдсан дүрсийн талбай нь $S=\fbox{cde}$ байна.
$A(1;1)$, $B(4;1)$, $C(4;5)$ цэгүүд гурвалжны оройнууд бол өнцгүүдийн косинусыг ол. $\overrightarrow{AB}(3;0)$, $\overrightarrow{AC}(3;4)$, $\overrightarrow{BC}(0;4)$ векторын уртыг олбол $|\overrightarrow{AB}|=\fbox{a}$, $|\overrightarrow{BC}|=\fbox{b}$, $|\overrightarrow{AC}|=\fbox{c}$. Хоёр векторын скаляр үржвэрийг олох томъёоноос $\cos\angle A=\dfrac{\fbox{d}}{\fbox{e}}; \cos\angle B=\fbox{f}; \cos\angle C=\dfrac{\fbox{g}}{\fbox{h}}$.
$x^2-6x+y^2-10y+9=0$ тойргийн $M(0;1)$ цэгт татсан шүргэгч шулуун ба түүнд татсан перпендикуляр шулууны тэгшитгэлийг бич. $(x-a)^2+(y-b)^2=r^2$ буюу тойргийн төв $A(\fbox{a};\fbox{b})$, тойргийн радиус $\fbox{c}$ болно. $AM$ шулууны тэгшитгэл нь $y=\dfrac{\fbox{d}}{\fbox{e}}x+1$ ба түүнд перпендикуляр $M(0;1)$ цэгийг дайрсан бидний олох шулууны тэгшитгэл нь $\fbox{f}x+\fbox{g}y-4=0$ болно.
Зургаас дараах функцийн
$$f(x)=\left\{\begin{array}{lll}\fbox{ab}, & x\le-2 & (2\text{ оноо)}\\ \fbox{c}\cdot x+\fbox{d}, & -2< x\le -1 & (2\text{ оноо)}\\ \fbox{e}\cdot x+\fbox{f}, & -1< x\le 0 & (2\text{ оноо)}\\ \fbox{g}, & x>0 & (1\text{ оноо)}\end{array}\right.$$


Координатын хавтгайд $A(1,2)$, $B(-1,1)$, $C(1,0)$, $D(-1,0)$ цэгүүд өгөв. $P(p,0)$ нь $CD$ хэрчим дээр орших ба $\angle APB$ өнцөг хамгийн их байхаар $P$ цэгийг олъё. $\alpha=\angle APC, \beta=\angle BPD, \theta=\angle APB$ гэвэл $\alpha+\beta+\theta=180^{\circ}$ ба $$\tg\alpha=\dfrac{\fbox{a}}{\fbox{b}-p},\tg\beta=\dfrac{\fbox{c}}{p+\fbox{d}}, \tg\theta=\dfrac{p+\fbox{e}}{p^2+\fbox{f}}$$ болно. Уламжлал авбал $(\tg\theta)'=-\dfrac{p^2+\fbox{g}p-1}{(p^2+\fbox{h})^2}$ болно. Эндээс $\theta$ өнцөг хамгийн их байх $P$ цэгийн координат $( \sqrt{\fbox{ij}}-\fbox{k},0)$ байна.
$A(1,1), B(-3,4), C(3,2)$ цэгүүд өгөв.
- $AB$ хэрчмийн урт $\fbox{a}$ байна.
- $AB$ шулууны тэгшитгэл $\fbox{b}x+\fbox{c}y-\fbox{d}=0$ байна.
- $C$ цэгээс $AB$ шулуун хүртэлх зай $\fbox{e}$ болно.
- $ABC$ гурвалжны талбай $\fbox{f}$ байна.
$A(1;1)$, $B(2;3)$, $C(4;-2)$ цэгүүд өгөгдөв. $AB$ хэрчмийн урт $\sqrt{\fbox{a}}$, $AB$ шулууны тэгшитгэл $\fbox{b}x-\fbox{c}y-1=0$ байна. $C$ цэгээс $AB$ шулуун хүртэлх зай $\dfrac{\fbox{d}}{\sqrt{\fbox{e}}}$ бөгөөд $ABC$ гурвалжны талбай нь $\dfrac{\fbox{f}}{\fbox{g}}$ байна.
$A(1;1), B(-3;4), C(3;2)$ цэгүүд өгөгдөв.
- $AB$ хэрчмийн урт $\fbox{a}$ байна.
- $AB$ шулууны тэгшитгэл $\fbox{b}x+\fbox{c}y-\fbox{d}=0$ байна.
- $C$ цэгээс $AB$ шулуун хүртэлх зай $\fbox{e}$ болно.
- $ABC$ гурвалжны талбай $\fbox{f}$ байна.
Хавтгайд хоорондоо 6 нэгж зайтай $A$ цэг ба $m$ шулуун байв.
- Энэ цэг ба шулуунаас ижил зайд байрлах цэгүүдийн олонлог нь $y=\dfrac{x^2}{\fbox{ab}}$ функцийн график болох муруйг дүрсэлнэ. $a,b$ хэд вэ?
- Энэ муруйн тэгш хэмийн тэнхлэгээс хоёр тийш 18 нэгж зайнд түүнтэй параллель байрлах $m_1$ ба $m_2$ шулуун болон $y=\dfrac{x^2}{\fbox{ab}}$ муруй, $m$ шулууны хооронд хашигдсан дүрсийн талбай нь $S=\fbox{cde}$ байна. $c; d; e$-г ол.
$x, y$ нь $x^2+y^2\leq 10$, $y\geq -2x+5$ нөхцлийг хангах үед $x+y$-ийн
хамгийн их утга $\fbox{a}\sqrt{\fbox{b}}$ ба хамгийн бага утга $\fbox{c}$ байна.
Хавтгай дээр хоорондоо 6 нэгж зайтай $A$ цэг ба $m$ шулуун байв.
- Энэ цэг ба шулуунаас ижил зайд байрлах цэгүүдийн олонлог нь $y=\dfrac{x^2}{\fbox{ab}}$ функцийн график болох муруйг дүрсэлнэ. $\text{a}$ ба $\text{b}$ нь хэд вэ?
- Энэ муруйн тэгш хэмийн тэнхлэгээс хоёр тийш 18 нэгж зайд түүнтэй параллель байрлах $m_1$ ба $m_2$ шулуун болон $y=\dfrac{x^2}{\fbox{ab}}$ муруй, $m$ шулууны хооронд хашигдсан дүрсийн талбай нь $S=\fbox{cde}$ байна.
Зургаас дараах функцийн $a,b,c,d,e,f,g$-г ол.
$$f(x)=\left\{\begin{array}{lll}\fbox{ab}, & x\le-2 & (2\text{ оноо)}\\ \fbox{c}\cdot x+\fbox{d}, & -2< x\le -1 & (2\text{ оноо)}\\ \fbox{e}\cdot x+\fbox{f}, & -1< x\le 0 & (2\text{ оноо)}\\ \fbox{g}, & x>0 & (1\text{ оноо)}\end{array}\right.$$
$$f(x)=\left\{\begin{array}{lll}\fbox{ab}, & x\le-2 & (2\text{ оноо)}\\ \fbox{c}\cdot x+\fbox{d}, & -2< x\le -1 & (2\text{ оноо)}\\ \fbox{e}\cdot x+\fbox{f}, & -1< x\le 0 & (2\text{ оноо)}\\ \fbox{g}, & x>0 & (1\text{ оноо)}\end{array}\right.$$

$A(2;3)$, $B(-2;0)$ бол $AB$ шулууны тэгшитгэл $\fbox{a}x-\fbox{b}y+\fbox{c}=0$ координатын эхээс $AB$ шулуун хүртэлх хамгийн богино зай $d=\dfrac{\fbox{d}}{\fbox{e}}$ байна.
Огторгуйн шулуунуудын хоорондох өнцөг
Огторгуйн шулууны тэгшитгэл
$A(0, 3, -1)$, $B(a^2, 5, a-1)$, $C(b, -1, b-1)$ гурван цэг нэг шулуун дээр орших бол $a$, $b$ тоог ол.
$A(1, -2, 1)$, $B(2, 1, 2)$, $C(x, y, y-1)$ гурван цэг өгөгдөв. $\overrightarrow{OC}$ вектор нь $\overrightarrow{OA}$,
$\overrightarrow{OB}$ векторуудад перпендикуляр байх бол $x$, $y$ ол. Мөн энэ тохиолдолд $OABC$ пирамидын эзлэхүүний ол. Үүнд $O$ координатын эх цэг болно.
$ A(1, 4, -2)$, $B(5, -1, -3)$, $C(2, 1, 3)$ гэсэн 3 цэг өгөгдөв.
- ${OAB}$ гурвалжны талбайг ол.
- $OC\perp(OAB)$ болохыг харуул.
- $OABC$ пирамидын эзлэхүүнийг ол.
$ A(1, 2, 3)$, $B(1, x, 10)$, $C(-3, 2, 4)$, $D(2, 4, 1)$ дөрвөн цэг нэг хавтгай дээр орших $x$ тоог ол.
$A(1,2,3)$, $B(-2,0,1)$ цэгүүдийг дайрсан шулууны вектор тэгшитгэлийг бич.
A. $\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}1\\2\\3\end{pmatrix}+t\begin{pmatrix}-3\\-2\\-2\end{pmatrix}$
B. $\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}1\\2\\3\end{pmatrix}+t\begin{pmatrix}-2\\ \phantom{-}0\\ \phantom{-}1\end{pmatrix}$
C. $\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}-2\\ \phantom{-}0\\ \phantom{-}1\end{pmatrix}+t\begin{pmatrix}1\\2\\3\end{pmatrix}$
D. $\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}-3\\-2\\-2\end{pmatrix}+t\begin{pmatrix}1\\2\\3\end{pmatrix}$
E. $\begin{pmatrix}x\\y\\z\end{pmatrix}=t\begin{pmatrix}3\\2\\2\end{pmatrix}-\begin{pmatrix}1\\2\\3\end{pmatrix}$
$\boldsymbol{r}=(3,8-2)+t(2,-1,3)$ ба $\boldsymbol{r}=(7,4,3)+s(2,1,4)$ хоёр шулууны харилцан байршлыг тодорхойл.
A. Параллел
B. $(9,5,-7)$ цэгт огтлолцоно
C. Давхцсан
D. Зөвхөн $(9,5,7)$ цэгт огтлолцоно
E. Координатын эх дээр огтлолцоно
$\boldsymbol{r}=(2,1,0)+t(1,2,3)$ ба $\boldsymbol{r}=(4,5,6)+s(2,4,6)$ хоёр шулууны харилцан байршлыг тодорхойл.
A. Параллел
B. Давхцсан
C. Солбисон
D. Зөвхөн $(2,1,0)$ цэгт огтлолцоно
E. $(1,2,3)$ цэгт огтлолцоно
$\boldsymbol{r}=(2,0,1)+t(-3,3,3)$ ба $\boldsymbol{r}=(1,3,0)+s(1,-1,1)$ хоёр шулууны харилцан байршлыг тодорхойл.
A. Зөвхөн $(-1,3,4)$ цэгт огтлолцоно
B. Давхцсан
C. Солбисон
D. Параллел
E. $(1,3,0)$ цэгт огтлолцоно
$\boldsymbol{r}=(2,8,0)+t(2,3,-1)$ ба $\boldsymbol{r}=(0,1,10)+s(-2,-3,1)$ хоёр шулууны харилцан байршлыг тодорхойл.
A. Параллел
B. Давхцсан
C. Солбисон
D. Зөвхөн $(6,6,6)$ цэгт огтлолцоно
E. $(1,2,3)$ цэгт огтлолцоно
Координатын эхээс $\boldsymbol{r}=(2,8,0)+t(2,3,-1)$ шулуун хүртэлх зайг ол.
A. $4$
B. $4.5$
C. $5$
D. $2\sqrt{3}$
E. $2\sqrt{5}$
$\boldsymbol{r}=(1,3-2)+t(1,4,9)$ ба $\boldsymbol{r}=(3,-1,2)+s(4,9,1)$ хоёр шулууны хоорондох өнцгийг ол.
A. $0^\circ$
B. $30^\circ$
C. $45^\circ$
D. $60^\circ$
E. $75^\circ$
$O(0,0,0)$, $A(-1,-2,7)$, $B(3,6,-3)$ цэгүүд өгөгдөв.
- $AB$ шулууны вектор тэгшитгэл $$\boldsymbol{r}=(-1,-2,7)+t(2,\fbox{a},-\fbox{b})$$ байна.
- $C\in AB$ ба $OC\perp AB$ байх $C$ цэгийн координатыг олбол $(\fbox{c},\fbox{d},\fbox{e})$ байна. Иймд $O$ цэгээс $AB$ шулуун хүртэлх зай $OC=\fbox{f}$ байна.
$O(0,0,0)$, $A(-2,-1,7)$, $B(6,3,-3)$ цэгүүд өгөгдөв.
- $AB$ шулууны вектор тэгшитгэл $$\boldsymbol{r}=(-2,-1,7)+t(\fbox{a},2,-\fbox{b})$$ байна.
- $C\in AB$ ба $OC\perp AB$ байх $C$ цэгийн координатыг олбол $(\fbox{c},\fbox{d},\fbox{e})$ байна. Иймд $O$ цэгээс $AB$ шулуун хүртэлх зай $OC=\fbox{f}$ байна.
Скаляр үржвэр
Ирмэгийн урт нь 1 байх зөв тетраэдр $OABC$-ийн хувьд $\overrightarrow{OA}=\vec{\mathstrut a}$, $\overrightarrow{OB}=\vec{\mathstrut b}$,
$\overrightarrow{OC}=\vec{\mathstrut c}$ гэе.
- $\vec{\mathstrut a}\cdot\vec{\mathstrut b}$ ол.
- $BC$-ийн дундаж нь $D$ бол $\overrightarrow{OA}\cdot\overrightarrow{OD}$ ол.
$2x-3y+4z=0$, $5x+6y+cz-3=0$ тэгшитгэлтэй хоёр хавтгай $c$-ийн ямар утганд харилцан перпендикуляр байх вэ?
A. $-2$
B. $3$
C. $2$
D. $-3$
E. $0$
$\vec{\mathstrut a}=(1;-3)$, $\vec{\mathstrut b}=(2;1)$ бол $2\vec{\mathstrut a}-3\vec{\mathstrut b}$, $\vec{\mathstrut a}+\vec{\mathstrut b}$ векторуудын скаляр үржвэрийг ол.
A. $36$
B. $-6$
C. $4$
D. $30$
E. $6$
$\overrightarrow{a\vphantom{b}}=(3;-1;2)$, $\overrightarrow{b}=(-1;y;4)$ ба $\overrightarrow{a\vphantom{b}}$, $\overrightarrow{b}$ векторууд перпендикуляр бол $y$-ийн утгыг ол.
A. $-5$
B. $-4$
C. $1$
D. $5$
E. $4$
$\overrightarrow{a\vphantom{b}}=(2;-1;3)$, $\overrightarrow{b}=(-1;y;4)$ ба $\overrightarrow{a\vphantom{b}}$, $\overrightarrow{b}$ векторууд перпендикуляр бол $y$-ийн утгыг ол.
A. $9$
B. $7$
C. $-10$
D. $10$
E. $0$
Тойргийн тэгшитгэл
$C\colon x^2+y^2=25$ тойрог ба $A(7,1)$ цэг өгөгдөв.
- $A$ цэгийг дайрсан, өнцгийн коэффициент нь 1 байх шулуун $C$ тойрогтой $P$, $Q$ цэгт огтлолцдох бол $PQ$ хэрчмийн уртыг ол.
- $A$ цэгээс $C$ тойрогт татсан шүргэгчийн шүргэлтийн цэгийг $T$ гэвэл $AT$ хэрчмийн уртыг ол.
$C_1\colon x^2+y^2=r^2\,(r>0)$, $C_2\colon x^2+y^2-6x+8y+16=0$ тойргууд хоёр ерөнхий цэгтэй байх $r$-ийн утгын мужийг ол.
$x^2+y^2=4 \boldsymbol{\cdots}(1)$, $x^2+y^2-2x+4y+3=0 \boldsymbol{\cdots}(2)$ тойргуудын огтлолцлын цэгүүд ба $(3,0)$ цэгийг дайрсан тойргийн тэгшитгэлийг бич.
$C(1,-1)$ цэгт төвтэй $3x-4y+3=0$ шулууныг шүргэх тойргийн тэгшитгэлийг бич. Мөн шүргэлтийн цэгийн координатыг ол.
- $x^2+y^2=50$ тойрог ба $3x+y-20=0$ шулууны огтлолцлын цэгийн координатыг ол.
- $x^2+y^2-4x-6y+9=0$ тойрог ба $x-3y=0$ шулууны огтлолцлын цэгийн тоог ол.
- $(3,-5)$ цэгт төвтэй, $r=6$ радиустай тойргийн тэгшитгэл бич.
- $x^2+y^2+5x-3y+6=0$ тойргийн төв, радиусыг ол.
Дараах тойргийн тэгшитгэлүүдийг бич.
- $(-3, 6)$, $(3,-2)$ цэгүүд нэг диаметрийн үзүүрүүд;
- $(-2,-1)$, $(4,-3)$, $(1, 2)$ цэгүүдийг дайрах.
- Дараах тойргийг өгөгдсөн цэгт шүргэх шүргэгч шулууны тэгшитгэлийг бич.
- $x^2+y^2=25$, $(3;4)$
- $(x-1)^2+(y-2)^2=25$, $(4;6)$
- $(-5, 10)$ цэгийг дайрах $x^2+y^2=25$ тойргийн шүргэгчийн тэгшитгэлийг бич.
$A(3, 1)$ цэгийг дайрах
$x^2+y^2=5$ тойргийг шүргэх хоёр шулууны шүргэлтийн цэгийг $P, Q$ гэвэл $PQ$ шулууны тэгшитгэл бич.
Хавтгайд $O(0,0)$, $A(1,2)$, $B(0,4)$, $C(4,2)$ цэгүүд өгөгдөв.
$\triangle OAB$, $\triangle OBC$-уудыг багтаасан тойргуудын радиусыг ол.
$P$ цэгт төвтэй, $r$ радиустай $C$ тойрог дараах хоёр
нөхцлийг хангаж байв.
- $C_1: x^2+y^2=1$, $C_2: x^2+y^2-6x+5=0$ тойргуудтай гадаад шүргэлцдэг.
- $P$ цэгийг координатын эхтэй холбоход үүсэх шулуун $x$ тэнхлэгтэй цагийн зүүний дагуу $60^{\circ}$ өнцөг үүсгэдэг.
$A(0,0)$ цэгт төвтэй 2 радиустай $A$ тойрог, $B(6,0)$ төвтэй 1 радиустай $B$ тойрог байв. $A$, $B$-г нэгэн зэрэг шүргэх шулууны тэгшитгэл бич.
$P$ цэгээс $C_1\colon x^2+y^2=3$, $C_2\colon (x-6)^2+y^2=9$ тойргуудад
татсан шүргэгчүүдийн уртын харьцаа $1:2$ байв. $P$ цэгийн геометр
байрыг ол.
$O(0,0)$ цэгт төвтэй $x^2+y^2=1$ тойрог дээрх $P(a,b)$, ($a>0$, $b>0$) цэгийн шүргэгч шулуун нь $x$ ба $y$ тэнхлэгүүдтэй харгалзан $A$, $B$ цэгүүдээр огтлолцсон бол $\triangle OAB$-ын талбайн хамгийн бага утгыг ол. Ямар $a$-ийн хувьд хамгийн бага утгаа авах вэ?
$C\colon x^2+(y-t)^2=4t-2$ ба $P(t,a)$ гэе.
- $t=1$ үед $P$ цэг $C$ тойргийн гадаад мужид байх $a$-ийн утгын мужийг ол.
- $2< t< 3$ үед $P$ цэг $C$ тойргийн дотоод мужид байх $a$-ийн утгын мужийг ол.
$A(1,1)$ цэгийг дайрч, $y$ тэнхлэгийг шүргэх $y=2x$ шулуун дээр төвтэй тойргийн тэгшитгэл бич.
$x^2+y^2=1$ тойрог $px+qy=1$ $(p>0, q>0)$ шулуунтай I мөчид шүргэлцдэг бол шулууны I мөчид орших
хэсгийг ординат тэнхлэгийг тойруулан эргүүлэхэд үүсэх биеийн эзлэхүүний хамгийн бага утгыг ол.
$x+y=1$ шулуун $x^2+y^2=a^2$ тойргийг шүргэх $a$-ийн утгуудыг ол.
Дараах тойргуудын тэгшитгэлийг бич.
- $(2,-3)$ цэгт төвтэй, $r=2$ радиустай;
- $(1,-2)$ цэгт төвтэй, координатын эхийг дайрах;
- $(-3,-4), (5, 8)$ цэгүүд нэг диаметрийн үзүүрүүд байх;
- $(-2, 6), (1,-3), (5,-1)$ цэгүүдийг дайрах.
$x^2+y^2-2x+6y-6=0$ тойргийн төв, радиусыг ол.
$x-y+1=0, x-3y-1=0, x+3y-7=0$ шулуунуудаар үүсэх гурвалжныг багтаасан тойрогт $(2, 5), (4, 1)$ цэгүүд харъяалагдах уу?
$x^2+y^2+2ax+3ay+13=0$ тэгшитгэл тойрог дүрслэх $a$ параметрийн утгын мужийг ол.
$2x-y-8=0$ шулуун дээр төвтэй $(0, 2)$, $(-1, 1)$ цэгүүдийг дайрах тойргийн тэгшитгэл бич.
Дараах тойргийн тэгшитгэлийг бич.
- $(2, 1)$ цэгт төвтэй, $x$ тэнхлэгийг шүргэх;
- $x, y$ тэнхлэгүүдийг шүргэж, $(2, 1)$ цэгийг дайрах.
Дараах тойрог ба шулуун нь ерөнхий цэгтэй бол түүний координатыг ол.
- $x^2+y^2=9$, $2x+3y-12=0$.
- $x^2+y^2+6x-4y+9=0$, $x-y+3=0$.
- $x^2+y^2-6x+8y=0$, $4x+3y=25$.
Дараах тойрог ба шулууны харилцан байршлыг $a$-аас хамааруулан тогтоо. Шүргэлцэх үед шүргэлтийн цэгийг ол.
- $x^2+y^2=5, y=2x+a$
- $x^2+y^2=1, y=a(x+2)$
Дараах тойргийг өгөгдсөн цэгт шүргэх шүргэгчийн тэгшитгэлийг бич.
- $x^2+y^2=4, (\sqrt{3},-1)$
- $x^2+y^2+8x-8y+19=0, (-2,1)$
$(2, 1)$ цэгээс $x^2+y^2=1$ тойрогт татсан шүргэгчийн тэгшитгэлийг бич.
Дараах шулуунуудын тэгшитгэлүүдийг бич.
- $x^2+y^2-2x-4y-4=0$ тойргийг шүргэх, 2 өнцгийн коэффициенттэй шулуун.
- $x^2+y^2+2x-6y+8=0$ тойргийг шүргэж, координатын эхийг дайрах.
$x^2+y^2=r^2$ тойргийн $m$-өнцгийн коэффициенттэй шүргэгчийн тэгшитгэл дараах хэлбэртэй болохыг батал. $y=mx\pm r\sqrt{m^2+1}$.
$x^2+y^2+x-6y-26=0$ тойрогтой ижил төвтэй, $x+2y-4=0$ шулууныг шүргэх тойргийн тэгшитгэл ба шүргэлтийн цэгийн координатыг ол.
$y=0$, $y=\sqrt{3}x$ шулуунуудыг шүргэж, $(3, 2\sqrt{3})$ цэгийг дайрах тойргийн тэгшитгэл бич.
Дараах хоёр тойргийн огтлолцлын цэгийн тоог ол. Хэрэв огтлолцох бол огтлолцлын цэгийн координатыг ол.
- $x^2+y^2=5$, $x^2+y^2+x+y=8$
- $x^2+y^2=13$, $x^2+y^2-12x-18y+65=0$
$x^2+y^2=25 \boldsymbol{\cdots}(1)$ бол
- Тойргийн төв нь $(12, 5)$ ба (1) тойргийг гадаад шүргэх тойргийн тэгшитгэл бич.
- Тойргийн төв нь $(1,-\sqrt{3})$ ба (1) тойргийг дотоод шүргэх тойргийн тэгшитгэл бич.
$x^2+y^2=4 \boldsymbol{\cdots}(1)$, $(x-a)^2+y^2=9 \boldsymbol{\cdots}(2)$ тойргуудын огтлолцлын цэгийн тоог $a$ параметрийн утгаас хамааруулж ол.
$x^2+y^2-3x-4y+1=0, x^2+y^2-5=0$ тойргуудын хувьд
- Огтлолцлын цэгүүдийг нь дайрах шулууны тэгшитгэл бич.
- Огтлолцлын цэгүүд ба $(1, 3)$ цэгийг дайрах тойргийн тэгшитгэл бич.
$x^2+y^2+2x-1=0$ тойрог ба $y=x+2$ шулууны огтлолцлын цэгүүд ба координатын эхийг дайрах тойргийн тэгшитгэл бич.
$C: x^2+y^2-2x-4y+4=0$ тойрог ба $\ell\colon y=mx+1$ шулууны огтлолцлын цэгүүд $\sqrt{2}$ зайтай бол $m$-ийн утгыг ол.
$a>0$ тогтмол тоо. $y=x^2$ парабол ба $x^2+(y-a)^2=1$ тойргууд шүргэлцэх $a$-параметрийн утгыг ол.
$b>a>0$, $p>0$ байг. Гадаад шүргэлцэх $x^2+(y-a)^2=r^2$, $x^2+(y-b)^2=s^2$ тойргууд нь $y=px^2$ параболыг тус бүрдээ хоёр
цэгээр шүргэх бол $p(s-r)=1$ болохыг батал.
$x^2+y^2+10x+12y+52=0$ тэгшитгэлээр өгсөн тойргийн талбайг ол.
A. $9\pi$
B. $10\pi$
C. $12\pi$
D. $16\pi$
E. $25\pi$
$x^2+y^2-4x+6y=3$ тойргийн төв $A$, радиус $r$ ол.
A. $A(4,6), r=\sqrt3$
B. $A(2,-3), r=4$
C. $A(-2,3), r=4$
D. $A(-4,6), r=\sqrt3$
E. $A(2,-3), r=\sqrt3$
$(x-1)^2+(y-2)^2=49$ тойрог дээр орших цэг аль нь вэ?
A. $(0;0)$
B. $(1;9)$
C. $(7;1)$
D. $(7;0)$
E. $(-1;9)$
$x^2+y^2+4y+1=0$ тэгшитгэлээр өгөгдсөн тойргийн радиусыг ол.
A. $1$
B. $-\sqrt2$
C. $\sqrt3$
D. $2$
E. $3$
$x^2+y^2-12x+10y+52=0$ тэгшитгэлээр өгсөн тойргийн талбайг ол.
A. $16\pi$
B. $9\pi$
C. $25\pi$
D. $12\pi$
E. $4\pi$
$x^2+y^2-4x+3=0$ тойргийн төв ба радиусыг заа.
A. $(2;1), R=1$
B. $(2;0), R=1$
C. $(0;1), R=2$
D. $(2;0), R=2$
E. $(2;1), R=2$
$x^2+y^2+2x+2y+1=0$ тойргийн төв ба радиусыг заа.
A. $(-1;-1), R=1$
B. $(1;1), R=1$
C. $(-1;-1), R=2$
D. $(1;-1), R=1$
E. $(-1;1), R=2$
$M(3;1)$, $N(-1;-5)$. $MN$ диаметртэй тойргийн тэгшитгэл аль
вэ?
A. $(x+1)^2+(y+2)^2=15$
B. $(x-1)^2+(y-2)^2=14$
C. $(x-1)^2+(y+2)^2=13$
D. $(x-1)^2+(y+2)^2=15$
E. $(x-1)^2+(y-2)^2=4^2$
$M(-2;3)$, $N(4;1)$. $MN$ диаметртэй тойргийн тэгшитгэл аль
вэ?
A. $(x-1)^2+(y-2)^2=9$
B. $(x-1)^2+(y-2)^2=10$
C. $(x+1)^2+(y-2)^2=11$
D. $(x-1)^2+(y-2)^2=12$
E. $(x+2)^2+(y-3)^2=40$
$(x-2)^2+(y+1)^2=2$ тэгшитгэлтэй тойрог дараах цэгүүдийн
алийг дайрах вэ?
A. $(2;-3)$
B. $(2;-1)$
C. $(1;-1)$
D. $(3;-2)$
E. $(3;2)$
$(x+2)^2+(y-1)^2=2$ тэгшитгэлтэй тойрог дараах цэгүүдийн
алийг дайрах вэ?
A. $(-2;1)$
B. $(-3;2)$
C. $(3;2)$
D. $(-3;-2)$
$(x-4)^2+(y-1)^2=9$, $(x-2)^2+(y-1)^2=1$ тэгшитгэлтэй хоёр
тойрог хэрхэн байрласныг заа.
A. хоёр цэгээр огтлолцсон
B. нэг нь нөгөөгийн дотор (ерөнхий цэггүй)
C. нэг ерөнхий цэгтэй
(шүргэлцсэн)
D. аль аль нь нөгөөгийн гадна (ерөнхий
цэггүй)
$(x-4)^2+(y-1)^2=16$, $(x-2)^2+(y-1)^2=4$ тэгшитгэлтэй хоёр
тойрог хэрхэн байрласныг заа.
A. нэг нь нөгөөгийн дотор (ерөнхий цэггүй)
B. хоёр цэгээр
огтлолцсон
C. аль аль нь нөгөөгийн гадна (ерөнхий цэггүй)
D. зөвхөн нэг цэгээр шүргэлцсэн
$2x-3y+4z-5=0$ хавтгай ба $MN$ хэрчмийн харилцан байршлыг
заа. үүнд: $M(1;1;1)$, $N(1;-1;1)$.
A. хавтгайн
эерэг талд оршино
B. хавтгайн сөрөг талд оршино
C. хавтгайтай огтлолцоно
D. хавтгайд харъяалагдана
$x^2+y^2-8x+6y+13=0$ тойргийн радиус хэд вэ?
A. 1
B. 2
C. 3
D. $\sqrt{12}$
E. $\dfrac{1}{2}$
$c$ параметрийн ямар утганд $x+y+c=0$ шулуун $x^2+y^2=1$ тойрогтой шүргэлцэх вэ?
A. $\sqrt2$
B. $1$
C. $-1$
D. $0$
E. $\pm2$
$x^2+y^2+2x+4y-20=0$ тэгшитгэлээр өгсөн тойргийн талбайг ол.
A. $9\pi$
B. $10\pi$
C. $12\pi$
D. $16\pi$
E. $25\pi$
Зурагт өгөгдсөн тойргийн тэгшитгэл бич.

A. $(x-4)^2+(y-3)^2=25$
B. $(x-4)^2+(y-3)^2=100$
C. $(x+3)^2+(y+4)^2=25$
D. $(x+4)^2+(y-3)^2=25$
E. $(x-3)^2+(y-4)^2=25$
Зурагт өгөгдсөн тойргийн тэгшитгэл бич.

A. $(x+4)^2+(y+3)^2=25$
B. $(x-4)^2+(y-3)^2=100$
C. $(x-4)^2+(y-3)^2=25$
D. $(x+4)^2+(y+3)^2=100$
E. $(x-3)^2+(y-4)^2=25$
$A(2,3)$ цэгээс $x^2-2x+y^2+4y+1=0$ тойрог хүртэлх хамгийн хол зайг ол.
A. 4
B. $\sqrt{26}$
C. $\sqrt{26}-2$
D. $\sqrt{26}+2$
E. 7
$x^2+y^2=13^2$ тойргийг $A(5;12)$ цэгт шүргэгч шулууны тэгшитгэл аль нь вэ?
A. $y=\dfrac{5}{12}x+\dfrac{119}{12}$
B. $y=-\dfrac{5}{13}x+\dfrac{181}{13}$
C. $12x+5y=169$
D. $5x+12y=169$
E. $x^2+12y=13^2$
$x^2+y^2+10x+12y+52=0$ тэгшитгэлээр өгсөн тойргийн талбайг ол.
A. $9\pi$
B. $10\pi$
C. $12\pi$
D. $16\pi$
E. $25\pi$
$A(1;1)$, $B(2;2)$ байг. $C\colon x^2+(y-a)^2=a^2$ тойрог $AB$ хэрчимтэй ерөнхий цэгтэй байх $a$ параметрийн утгын мужийг ол.
A. $[-1,2]$
B. $[-2;2]$
C. $]-1;2[$
D. $[1;2]$
E. $]1;2[$
$(x-4)^2+(y-3)^2=49$ нь $\fbox{(a;b)}$ төвтэй $\fbox{c}$ радиустай тойргийн тэгшитгэл ба $A(x;y)$ нь тойргийн цэг үед $3x+4y$ илэрхийллийн хамгийн бага утга нь $\fbox{def}$ юм.
Координатын эх дээр төвтэй $r$ радиустай тойрог $12x+5y-169=0$ шулууныг шүргэж байв.
- Тойргийн радиус $\fbox{ab}$ байна.
- Тойргийн төв ба шүргэлтийн цэгийг дайрсан шулууны тэгшитгэл $\fbox{c}x-\fbox{de}y=0$.
- Шүргэлтийн цэгийн координат нь $(\fbox{fg},\fbox{h})$ байна.
$(x-4)^2+(y-3)^2=49$ нь $(\fbox{a};\fbox{b})$ төвтэй $\fbox{c}$ радиустай тойргийн тэгшитгэл ба $A(x;y)$ нь тойргийн цэг үед $3x+4y$ илэрхийллийн хамгийн их утга нь $\fbox{de}$ юм.
$(x-1)^2+(y-2)^2=25$ нь $O(\fbox{a},\fbox{b})$ төвтэй $\fbox{c}$ радиустай тойргийн тэгшитгэл байна. $A(5;-1)$ бол $\overrightarrow{OA}$ векторын координат нь $(\fbox{d},-\fbox{e})$ болох тул тойргийн $A$ цэгт татсан шүргэгч шулууны тэгшитгэл нь $\fbox{f}x-\fbox{g}y-23=0$ байна.
$x^2+y^2=16$ тэгшитгэлтэй тойрогт $A(0;5)$ цэгээс татсан
шүргэгчүүдийн тэгшитгэл $\fbox{a}x+\fbox{bc}y+20=0$,
$\fbox{d}x+\fbox{e}y-20=0$ байна.
$C\colon x^2+y^2=4$ тойрог, $\ell\colon ax-y-4a+2=0$ шулуун хоёр 2 цэгээр огтлолцох $a$ параметрийн утгын муж нь $\fbox{a}< a<\dfrac{\fbox{b}}{\fbox{c}}$ байна.
$A(-6;1)$, $B(2;5)$, $C(3;-2)$ цэгүүдэд оройтой гурвалжин байв.
- $C$ оройн медианы тэгшитгэл $y=-\fbox{a}x+1$ бол $a$-г ол.
- $\overrightarrow{AC}$, $\overrightarrow{AB}$ векторын хоорондох өнцөг болох $A$ оройн дотоод өнцгийг $\alpha$ гэвэл $\alpha=\fbox{bc}^\circ$ байна.
- Гурвалжныг багтаасан тойргийн тэгшитгэл нь $$(x+\fbox{d})^2+(y-\fbox{e})^2=\fbox{f}^2$$
$f(x)=x^2-8x+17$ функц өгөгдөв.
- $f(x)$ функцийн $x_0=5$ абсцисстэй $M$ цэгт татсан шүргэгч шулууны тэгшитгэл $y=\fbox{a}x-\fbox{b}$ (2 оноо).
- $f(x)$ функцийн график, дээрх шүргэгч шулуун болон координатын тэнхлэгүүдээр хүрээлэгдсэн дүрсийн талбай $\dfrac{\fbox{cd}}{3}$ (2 оноо).
- $f(x)$ функцийн графикийг $M$ цэгт шүргэх, төв нь $OX$ (абсцисс) тэнхлэг дээр орших тойргийн тэгшитгэл $(x-\fbox{e})^2+y^2=\fbox{fg}$ (3 оноо).
Хавтгайн векторуудын харилцан байршил
$\overrightarrow{a\vphantom{b}}=(x;1;-3)$, $\overrightarrow{b}=(-2;y;1)$ ба $\overrightarrow{a\vphantom{b}}$, $\overrightarrow{b}$ векторууд перпендикуляр бол бол $-2x+y$-ийн утгыг ол.
A. $-2$
B. $-3$
C. $1$
D. $2$
E. $3$
Хавтгайн тэгшитгэл
$5x+3y+z+7=0$ хавтгай ба $M(2;-3;-7)$ цэгийн харилцан
байршил аль вэ?
A. $M$ цэг хавтгайд харъяалагдана
B. $M$ цэг хавтгайн сөрөг талд оршино
C. $M$ цэг хавтгайн эерэг талд оршино
D. Перпендикуляр
E. Өмнөх дөрвийн аль нь ч биш
$P(1;1;4)$, $Q(5;1;0)$, $R(7;5;2)$ гурван цэгийг дайрсан
хавтгайн тэгшитгэл аль вэ?
A. $x+y+z-4=0$
B. $x+y-z-4=0$
C. $x-y+z-4=0$
D. $x-y+z+4=0$
E. $x-y-z-4=0$
$P(2,3,1)$, $Q(1,5,2)$, $R(0,7,3)$ гурван цэгийг дайрсан хавтгайн тэгшитгэл аль вэ?
A. $x-2y-3z-5=0$
B. $x+2y+3z-5=0$
C. $x+2y-3z+5=0$
D. $x+2y-3z-5=0$
E. $x-2y-3z+5=0$
$2x-3y+4z=0$, $5x+6y+cz-3=0$ тэгшитгэлтэй хоёр хавтгай $c$-ийн ямар утганд харилцан перпендикуляр байх вэ?
A. $-2$
B. $3$
C. $2$
D. $-3$
E. $0$
$x+y-2z+5=0$ хавтгай $Oz$ тэнхлэгтэй огтлолцсон цэг аль вэ?
A. $(1,0,2.5)$
B. $(2.5,1,0)$
C. $(2.5,0,0)$
D. $(0,0,2.5)$
E. $(0,2.5,0)$
$3x-4y+5z-8=0$ хавтгай $Oy$ тэнхлэгтэй огтлолцох цэг аль вэ?
A. $(2,0,0)$
B. $(0,0,-2)$
C. $(0,-2,0)$
D. $(0,2,0)$
E. $(1,0,1)$
$3x-4y+5z+12=0$ хавтгай $Ox$ ба $Oy$ тэнхлэгтэй огтлолцсон
хоёр цэгийн хоорондох зай аль вэ?
A. $4$
B. $5$
C. $6$
D. $7$
E. $10$
$5x+3y-4z+12=0$ хавтгай $Oy$, $Oz$ тэнхлэгтэй огтлолцох хоёр
цэгийн хоорондох зай аль вэ?
A. $3$
B. $4$
C. $5$
D. $6$
E. $10$
$x-y+z-5=0$, $3x+4y-z-2=0$ тэгшитгэлтэй хоёр хавтгайн
огтлолын шулуун дээр аль цэг оршихыг заа.
A. $(2,2,5)$
B. $(1,2,9)$
C. $(1,1,5)$
D. $(3,4,0)$
E. $(2,2,6)$
$3x+4y-5z+2=0$, $y-3z+4=0$ тэгшитгэлтэй хоёр хавтгайн огтлолцол дээр орших цэг аль вэ?
A. $(2,2,2)$
B. $(0,2,2)$
C. $(1,0,1)$
D. $(1,2,3)$
E. $(0,-3,-2)$
$2x-y+z-5=0$, $3x+4y+z-11=0$, $x-y+z-4=0$ тэгшитгэлтэй гурван хавтгайн огтлолцлын цэг аль вэ?
A. $(1,-3,0)$
B. $(6,0,-7)$
C. $(5,11,4)$
D. $(2,1,2)$
E. $(1,1,4)$
$5x-3y+2z=0$, $3x+2y-6z-8=0$, $7x-2y-3z-3=0$ тэгшитгэлтэй
гурван хавтгайн огтлолын цэг аль вэ?
A. $(1;1;-1)$
B. $(2;4;1)$
C. $(6;4;3)$
D. $(0;3;-2)$
$A(1,3,-2)$, $B(3,-9,7)$, $C(4,-4,5)$ цэгүүдийг дайрсан хавтгайн тэгшитгэл бич.
A. $21x-13y-22z+26=0$
B. $x+y+z-2=0$
C. $21x-13y+22z-26=0$
D. $3x+2y+2z-5=0$
E. $21x-13y-22z-26=0$
$\boldsymbol{r}=i+j+3k+t(2i+j-k)$ шулуун ба $2x+y-5z=8$ хавтгайн харилцан байршлыг тодорхойл. Хэрэв огтлолцох бол огтлолцлын цэгийг ол.
A. Шулуун хавтгайд агуулагдана
B. Параллел
C. $(5,3,1)$ цэгт огтлолцоно
D. $(3,2,2)$ цэгт огтлолцоно
E. Дээрхийн аль нь ч биш
$\boldsymbol{r}=i+j+3k+t(3i+2j-k)$ шулуун ба $4x-y+10z=2$ хавтгайн харилцан байршлыг тодорхойл. Хэрэв огтлолцох бол огтлолцлын цэгийг ол.
A. Шулуун хавтгайд агуулагдана
B. Параллел
C. Координатын эх дээр огтлолцоно
D. $(1,1,3)$ цэгт огтлолцоно
E. Дээрх хариултуудын аль нь ч биш
$\boldsymbol{r}=i+j+3k+t(2i+j-k)$ шулуун ба $x+2y+4z=15$ хавтгайн харилцан байршлыг тодорхойл. Хэрэв огтлолцох бол огтлолцлын цэгийг ол.
A. Шулуун хавтгайд агуулагдана
B. Параллел
C. Координатын эх дээр огтлолцоно
D. $(1,1,3)$ цэгт огтлолцоно
E. Дээрх хариултуудын аль нь ч биш
$\alpha_1\colon 2x-3y+4z=7$ ба $\alpha_2\colon 3x-4y+2z=5$ хавтгайнуудын харилцан байршлыг тодорхойл, хэрэв огтлолцох бол огтлолцолын шулууны вектор тэгшитгэлийг ол.
A. Огтлолцоно, $\boldsymbol{r}=(2,-3,4)+t(3,-4,2)$
B. Параллел
C. Харилцан перпендикуляр
D. Давхцана
E. Огтлолцоно, $\boldsymbol{r}=(7,5,2)+t(10,8,1)$
$\boldsymbol{r}=2i+j-k+t(2i-7j-5k)$ шулуун ба $-3x+4y+z=10$ хавтгайн хоорондох өнцгийг ол.
A. $30^\circ$
B. Параллел
C. $45^\circ$
D. $60^\circ$
E. $90^\circ$
$x+4y+3z-12=0$, $7x+2y+8z-5=0$ хавтгайнуудын хоорондох өнцгийг ол.
A. $0^\circ$
B. $15^\circ$
C. $30^\circ$
D. $45^\circ$
E. $60^\circ$
$\alpha_1\colon 2x-11y+10z-15=0$, $\alpha_2\colon 2x-11y+10z+45=0$ бол $\alpha_1$, $\alpha_2$ хавтгайнуудын хоорондох зайг ол.
A. $0$
B. $1$
C. $2$
D. $3$
E. $4$
Дараах $OZ$ тэнхлэг дээр цэгүүдийн алинаас нь $2x-3y+6z-4=0$ хавтгай хүртэлх зай 2-той тэнцүү байх вэ?
A. $(0,0,4)$
B. $(0,0,-2)$
C. $\left(0,0,-\frac53\right)$
D. $(0,0,3)$
E. $\left(0,0,5\frac13\right)$
$M(1,1,-1)$ цэгийг дайрсан $2x-y+5z+3=0$, $x+3y-z-7=0$ хавтгайнуудад перпендикуляр хавтгайн тэгшитгэл аль вэ?
A. $-2x+y+z+2=0$
B. $2x-y-z-4=0$
C. $2x-y-z+4=0$
D. $-2x+y+z-2=0$
E. $x-2y-3z+5=0$
2. $ M(2, 0, -3) $ цэгийг дайрсан
a. $ \vec{\mathstrut a}= (2, -3, 5) $ вектортой паралель
б. $ \vec{\mathstrut r}= (1, -2, -1) + t(5, 2, -1)$ шулуунтай параллель,
в. $ Ox $ тэнхлэгтэй параллель шулууны параметр тэгшитгэлийг бич.
a. $ \vec{\mathstrut a}= (2, -3, 5) $ вектортой паралель
б. $ \vec{\mathstrut r}= (1, -2, -1) + t(5, 2, -1)$ шулуунтай параллель,
в. $ Ox $ тэнхлэгтэй параллель шулууны параметр тэгшитгэлийг бич.
$ M(2, 0, -3) $ цэгийг дайрсан
a. $ \vec{\mathstrut a}= (2, -3, 5) $ вектортой паралель
б. $ \vec{\mathstrut r}= (1, -2, -1) + t(5, 2, -1)$ шулуунтай параллель,
в. $ Ox $ тэнхлэгтэй параллель шулууны параметр тэгшитгэлийг бич.
a. $ \vec{\mathstrut a}= (2, -3, 5) $ вектортой паралель
б. $ \vec{\mathstrut r}= (1, -2, -1) + t(5, 2, -1)$ шулуунтай параллель,
в. $ Ox $ тэнхлэгтэй параллель шулууны параметр тэгшитгэлийг бич.
3. $M_1 $, $M_2 $ цэгүүдийг дайрсан шулууны хялбар тэгшитгэлийг бич.
a. $ M_1(1. -2, 1)$, $M_2(3, 1, -1)$
б. $ M_1(3. -1, 0)$, $M_2(1, 0, -3)$
в. $ M_1(-1. 2, 3)$, $M_2(2, 6, -2)$
a. $ M_1(1. -2, 1)$, $M_2(3, 1, -1)$
б. $ M_1(3. -1, 0)$, $M_2(1, 0, -3)$
в. $ M_1(-1. 2, 3)$, $M_2(2, 6, -2)$
4. Дараах шулуунуудын харилцан байршлыг тодорхойл.
a. $ \frac{x+3}{3} = \frac{y-1}{-2} = \frac{z}{1}$ ба $ \vec{\mathstrut a}= (-2, 0, -2) +t(-6, 4, -2) $
б. $ \frac{x+3}{1} = \frac{y+1}{2} = \frac{z+1}{1}$ ба $\left\{\begin{array}{c} x=-4+3t\\ y=2+t\\ z=t \end{array}\right.$
в. $ \vec{\mathstrut r}= (1, -1, 0) +t(2, 3, 1) $ ба $ \vec{\mathstrut r}= (0, 2, 1) +s(-1, 2, 3) $
г. $ \vec{\mathstrut r}= (1, -2, -3) +t(2, 1, -2) $ ба $\left\{\begin{array}{c} x=-3+4t\\ y=-4+2t\\ z= 1 -4t \end{array}\right.$
д. $\frac{x}{1} = \frac{y-1}{-2} = \frac{z}{3}$ ба $\frac {x-1}{1} = \frac{y-1}{2}=\frac{z-1}{1}$
a. $ \frac{x+3}{3} = \frac{y-1}{-2} = \frac{z}{1}$ ба $ \vec{\mathstrut a}= (-2, 0, -2) +t(-6, 4, -2) $
б. $ \frac{x+3}{1} = \frac{y+1}{2} = \frac{z+1}{1}$ ба $\left\{\begin{array}{c} x=-4+3t\\ y=2+t\\ z=t \end{array}\right.$
в. $ \vec{\mathstrut r}= (1, -1, 0) +t(2, 3, 1) $ ба $ \vec{\mathstrut r}= (0, 2, 1) +s(-1, 2, 3) $
г. $ \vec{\mathstrut r}= (1, -2, -3) +t(2, 1, -2) $ ба $\left\{\begin{array}{c} x=-3+4t\\ y=-4+2t\\ z= 1 -4t \end{array}\right.$
д. $\frac{x}{1} = \frac{y-1}{-2} = \frac{z}{3}$ ба $\frac {x-1}{1} = \frac{y-1}{2}=\frac{z-1}{1}$
$ M(2, 3, -1) цэгээс дараах шулуун хүртэлх зайг ол.
a. $ \frac{x-5}{3} = \frac{y}{2} = \frac{z +25}{-2} $
$ \left\{\begin{array}{c} x=t +1\\ y= t +2\\ z=4t + 13 \end{array}\right.$
в. $ \vec{\mathstrut r}= (1, -5, -15) +t(1,1, -1) $
a. $ \frac{x-5}{3} = \frac{y}{2} = \frac{z +25}{-2} $
$ \left\{\begin{array}{c} x=t +1\\ y= t +2\\ z=4t + 13 \end{array}\right.$
в. $ \vec{\mathstrut r}= (1, -5, -15) +t(1,1, -1) $
9. a. $ M (2, 1, -1) $ , $ \vec{\mathstrut n}= (1, -2, 3) $
б. $ M (2, 3, 5) $, $ \vec{\mathstrut n}= \vec{\mathstrut 4i} + \vec{\mathstrut 3j} +\vec{\mathstrut 2k}$
б. $ M (2, 3, 5) $, $ \vec{\mathstrut n}= \vec{\mathstrut 4i} + \vec{\mathstrut 3j} +\vec{\mathstrut 2k}$
10. Координатын эхээс хавтгайд буулгасан перпендикулярын суурийн цэг $N(3, 5, 2)$ бол хавтгайн тэгшитгэлийг бич .
11. $ A(3, -1, 2)$ , $ B(4, -2, -1) $ цэгүүд өгөгдөв. $A$ цэгийг дайрсан $\vec{\mathstrut AB}$ векторт перпендикуляр хавтгайн тэгшитгэл зохио.
12. $ (M_0=(3,4,-5)$ цэгийг дайрсан $\vec{\mathstrut a}= (3, -1, 2) $, $\vec{\mathstrut b}= (1, 2, -1) $ векторуудтай параллель хавтгайн тэгшитгэл бич.
13. Дараах цэгүүдийг дайрсан хавтгайн тэгшитгэл бич.
a. $ A(2, 1, 3)$ , $ B( 2, 4, 0) $ , $C( -3, 0, 4) $
б. $ A(1, 3, -2)$ , $ B( 3, -9, 7) $ , $C( 4, -4, 5) $
в. $ A(3, -4, 7)$ , $ B( -5, 3, -2) $ , $C( 1, 2, -3) $,
a. $ A(2, 1, 3)$ , $ B( 2, 4, 0) $ , $C( -3, 0, 4) $
б. $ A(1, 3, -2)$ , $ B( 3, -9, 7) $ , $C( 4, -4, 5) $
в. $ A(3, -4, 7)$ , $ B( -5, 3, -2) $ , $C( 1, 2, -3) $,
13. Дараах цэгүүдийг дайрсан хавтгайн тэгшитгэл бич.
a. $ A(2, 1, 3)$, $ B(2, 4, 0) $, $ C(-3, 0, 4 ) $
б. $ A(1, 3, -2)$, $ B(3, -9, 7)$, $ C(4, -4, 5) $
в. $ A(1, 3, -2)$, $ B(3, -9, 7)$, $ C(4, -4, 5) $
a. $ A(2, 1, 3)$, $ B(2, 4, 0) $, $ C(-3, 0, 4 ) $
б. $ A(1, 3, -2)$, $ B(3, -9, 7)$, $ C(4, -4, 5) $
в. $ A(1, 3, -2)$, $ B(3, -9, 7)$, $ C(4, -4, 5) $
14. $ \frac{x-2}{1}=\frac{y-3}{2}=\frac{z+1}{2} $ шулуун ба $ A(3, 4, 0)$ цэгийг дайрсан хавтгайн тэгшитгэлийг бич.
15. $ M_0(2, -2, 1)$ цэгийг дайрсан $ \frac{x-1}{2}=\frac{y-2}{-3}=\frac{z+3}{2} $ шулууныг дайрсан хавтгайн тэгшитгэл зохио.
16. $ \frac{x-1}{1}=\frac{y+1}{2}=\frac{z+2}{2} $ шулууныг дайрсан $ 2x +3y-z-4=0 $ хавтгайд перпендикуляр хавтгайн тэгшитгэлийг бич.
15. Өгөгдсөн цэгүүдийг дайрсан өгөгдсөн хавтгайд перпендикуляр хавтгайн тэгшитгэлийг бич.
a. $ M(1, -1, 0) $ , $ N(1, -2, 5) $ , $ 2x +3y-4z+7=0 $
б. $ M(1, 3, 2) $ , $ N(2, -3, 2) $ , $ x - 2y +2z-3=0 $
a. $ M(1, -1, 0) $ , $ N(1, -2, 5) $ , $ 2x +3y-4z+7=0 $
б. $ M(1, 3, 2) $ , $ N(2, -3, 2) $ , $ x - 2y +2z-3=0 $
19. $ M_0(1, 2, 3) $ цэг ба коордиантын $Ox$ тэнхлэгийг дайрсан хавтгайн тэгшитгэл зохио.
20. $ M_0(1, 3, -1)$ цэгийг дайрч $ 2x +y-3z+4=0 $ $ x-y+5z-1=0$ хавтгайнууд перпендикуляр байх хавтгайн тэгшитгэл бич.
21. $ 2x-6y+4z=7$ ба $ 3x -4y+2z=5$ хавтгайн харилцан байршлыг тодорхойл. Хэрэв огтлолцох бол огтлолцлын шулууны вектор тэгшитгэлийг бич.
$\ell\colon\boldsymbol{r}=(1,0,-1)+t(2,1,0)$ шулуун ба $M(0,1,2)$ цэг өгөгдөв.
- $\ell$ шулуун ба $M$ цэгийг дайрсан хавтгайн тэгшитгэл бич. $$x-\fbox{a}y+\fbox{b}z=0$$
- $M$ цэгийг дайрсан $\ell$ шулуунд перпендикуляр хавтгайн тэгшитгэл бич. $$\fbox{c}x+\fbox{d}y-1=0$$
- $M$ цэгийг дайрсан $\ell$ шулуунтай параллел шулууны тэгшитгэл бич. $$\boldsymbol{r}=(0,1,\fbox{e})+t(\fbox{f},1,\fbox{g})$$
$\ell\colon\boldsymbol{r}=(1,0,-1)+t(2,1,0)$ шулуун ба $M(-2,1,-3)$ цэг өгөгдөв.
- $M$ цэгээс $\ell$ шулуун хүртэлх зай $\fbox{a}$ байна.
- $\ell$ шулууны хувьд $M$ цэгтэй тэгш хэмтэй цэг нь $(\fbox{b},-\fbox{c},\fbox{d})$ байна.
$\ell\colon\boldsymbol{r}=(0,-1,1)+t(2,4,1)$ шулуун ба $M(1,-2,0)$ цэг өгөгдөв.
- $\ell$ шулуун ба $M$ цэгийг дайрсан хавтгайн тэгшитгэл бич. $$x-\fbox{a}y+\fbox{b}z-3=0$$
- $M$ цэгийг дайрсан $\ell$ шулуунд перпендикуляр хавтгайн тэгшитгэл бич. $$\fbox{c}x+\fbox{d}y+z+\fbox{e}=0$$
- $M$ цэгийг дайрсан $\ell$ шулуунтай параллел шулууны тэгшитгэл бич. $$\boldsymbol{r}=(\fbox{e},-2,0)+t(\fbox{f},\fbox{g},1)$$
Цэгээс хавтгай хүртэлх зай
$\alpha_1\colon 2x-11y+10z-15=0$, $\alpha_2\colon 2x-11y+10z+45=0$ бол $\alpha_1$, $\alpha_2$ хавтгайнуудын хоорондох зайг ол.
A. $0$
B. $1$
C. $2$
D. $3$
E. $4$
Дараах $OZ$ тэнхлэг дээр цэгүүдийн алинаас нь $2x-3y+6z-4=0$ хавтгай хүртэлх зай 2-той тэнцүү байх вэ?
A. $(0,0,4)$
B. $(0,0,-2)$
C. $\left(0,0,-\frac53\right)$
D. $(0,0,3)$
E. $\left(0,0,5\frac13\right)$
Цэгээс шулуун хүртэлх зай
$A(0,-2)$, $B(4,0)$ цэгүүд ба $y=x^2$ парабол дээр хөдөлж буй $P$ цэгүүдээр
тодорхойлогдох $S_{\triangle PAB}$-ийн хамгийн бага утгыг ол.
Цэгээс шулуун хүртэлх зайг ол.
- $O(0, 0)$ цэгээс $4x+3y-12=0$
- $(2,-3)$ цэгээс $2x-3y+5=0$
- $(-1, 3)$ цэгээс $x=2$
- $(5, 6)$ цэгээс $y=3$
$x-2y+3=0$, $x-2y-1=0$ шулуунуудын хоорондын зайг ол.
$y=x^2+1$ параболын $P$ цэг ба $x+y+1=0$ шулууны
$Q$ цэг хоёрын хоорондын зайн хамгийн бага утгыг ол.
Координатын хавтгайд $A(-1,1)$ ба $B(3,4)$ цэгүүд өгөв. $O(0,0)$ цэгээс $AB$ шулуун хүрэх хамгийн богино зайг ол.
A. $\dfrac85$
B. $1.4$
C. $\sqrt3$
D. $0.8$
E. $\sqrt2$
$(5,-1)$ цэгээс $ax-4y-4=0$ шулуун хүртэлх зай 3 байх $a$
параметрийн утгыг ол.
A. $a=\pm 3$
B. $a=0$
C. $a=\pm\sqrt3$
D. $a=\pm\sqrt5$
E. $a=\pm 2$
Координатын эхээс $\boldsymbol{r}=(2,8,0)+t(2,3,-1)$ шулуун хүртэлх зайг ол.
A. $4$
B. $4.5$
C. $5$
D. $2\sqrt{3}$
E. $2\sqrt{5}$
$A(1,1), B(-3,4), C(3,2)$ цэгүүд өгөв.
- $AB$ хэрчмийн урт $\fbox{a}$ байна.
- $AB$ шулууны тэгшитгэл $\fbox{b}x+\fbox{c}y-\fbox{d}=0$ байна.
- $C$ цэгээс $AB$ шулуун хүртэлх зай $\fbox{e}$ болно.
- $ABC$ гурвалжны талбай $\fbox{f}$ байна.
$A(1;1)$, $B(2;3)$, $C(4;-2)$ цэгүүд өгөгдөв. $AB$ хэрчмийн урт $\sqrt{\fbox{a}}$, $AB$ шулууны тэгшитгэл $\fbox{b}x-\fbox{c}y-1=0$ байна. $C$ цэгээс $AB$ шулуун хүртэлх зай $\dfrac{\fbox{d}}{\sqrt{\fbox{e}}}$ бөгөөд $ABC$ гурвалжны талбай нь $\dfrac{\fbox{f}}{\fbox{g}}$ байна.
Шулуун ба хавтгайн хоорондох өнцөг
1. $ M(1, -1, 3)$ цэгийг дайрсан
a. $ \vec{\mathstrut a}= (2, -3, 4)$ вектортой параллель
б. $ \frac{x-1}{2} = \frac{y+2}{4}=\frac{z-1}{0}$ шулуунтай параллель
в. $ x = 3t - 1$ , $ y = -2t + 3 $, $ z = 5t + 2 $ шулуунтай параллель шулууны вектор тэгшитгэлийг бич.
a. $ \vec{\mathstrut a}= (2, -3, 4)$ вектортой параллель
б. $ \frac{x-1}{2} = \frac{y+2}{4}=\frac{z-1}{0}$ шулуунтай параллель
в. $ x = 3t - 1$ , $ y = -2t + 3 $, $ z = 5t + 2 $ шулуунтай параллель шулууны вектор тэгшитгэлийг бич.
Шулууны вектор тэгшитгэл
$A(1,2,3)$, $B(-2,0,1)$ цэгүүдийг дайрсан шулууны вектор тэгшитгэлийг бич.
A. $\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}1\\2\\3\end{pmatrix}+t\begin{pmatrix}-3\\-2\\-2\end{pmatrix}$
B. $\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}1\\2\\3\end{pmatrix}+t\begin{pmatrix}-2\\ \phantom{-}0\\ \phantom{-}1\end{pmatrix}$
C. $\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}-2\\ \phantom{-}0\\ \phantom{-}1\end{pmatrix}+t\begin{pmatrix}1\\2\\3\end{pmatrix}$
D. $\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}-3\\-2\\-2\end{pmatrix}+t\begin{pmatrix}1\\2\\3\end{pmatrix}$
E. $\begin{pmatrix}x\\y\\z\end{pmatrix}=t\begin{pmatrix}3\\2\\2\end{pmatrix}-\begin{pmatrix}1\\2\\3\end{pmatrix}$
$\boldsymbol{r}=(3,8-2)+t(2,-1,3)$ ба $\boldsymbol{r}=(7,4,3)+s(2,1,4)$ хоёр шулууны харилцан байршлыг тодорхойл.
A. Параллел
B. $(9,5,-7)$ цэгт огтлолцоно
C. Давхцсан
D. Зөвхөн $(9,5,7)$ цэгт огтлолцоно
E. Координатын эх дээр огтлолцоно
$\boldsymbol{r}=(2,1,0)+t(1,2,3)$ ба $\boldsymbol{r}=(4,5,6)+s(2,4,6)$ хоёр шулууны харилцан байршлыг тодорхойл.
A. Параллел
B. Давхцсан
C. Солбисон
D. Зөвхөн $(2,1,0)$ цэгт огтлолцоно
E. $(1,2,3)$ цэгт огтлолцоно
$\boldsymbol{r}=(2,0,1)+t(-3,3,3)$ ба $\boldsymbol{r}=(1,3,0)+s(1,-1,1)$ хоёр шулууны харилцан байршлыг тодорхойл.
A. Зөвхөн $(-1,3,4)$ цэгт огтлолцоно
B. Давхцсан
C. Солбисон
D. Параллел
E. $(1,3,0)$ цэгт огтлолцоно
$\boldsymbol{r}=(2,8,0)+t(2,3,-1)$ ба $\boldsymbol{r}=(0,1,10)+s(-2,-3,1)$ хоёр шулууны харилцан байршлыг тодорхойл.
A. Параллел
B. Давхцсан
C. Солбисон
D. Зөвхөн $(6,6,6)$ цэгт огтлолцоно
E. $(1,2,3)$ цэгт огтлолцоно
$\boldsymbol{r}=(1,3-2)+t(1,4,9)$ ба $\boldsymbol{r}=(3,-1,2)+s(4,9,1)$ хоёр шулууны хоорондох өнцгийг ол.
A. $0^\circ$
B. $30^\circ$
C. $45^\circ$
D. $60^\circ$
E. $75^\circ$
Шулууны өнцгийн коэффициент
$ -2$, $ 2$ , $ 1$ тоонууд язгуур нь болох $ 3$ зэргийн олон гишүүнт аль вэ?
A. $ x^3-2x^2-x+2$
B. $ x^3+x^2-4x+4 $
C. $ x^3+3x^2-4x-12 $
D. $ x^3-x^2-4x+4 $
E. $ x^3+x^2+4x-4 $
$A(3; 0)$, $B(0; -2)$ цэгүүдийг дайрсан шулууны налалтыг олоорой.
A. $3$
B. $-\frac{2}{3}$
C. $\frac{2}{3}$
D. $-3$
E. $-6$
$A(-2; 0)$, $B(0; -1)$ цэгүүдийг дайрсан шулууны налалтыг олоорой.
A. $-\dfrac{3}{2}$
B. $\dfrac{1}{2}$
C. ${2}$
D. $-2$
E. $-3$
$A( -2; 0)$, $B(0; -1)$ цэгүүдийг дайрсан шулууны налалтыг олоорой.
A. $ -\frac12$
B. $ \frac{1}{2}$
C. $ 2$
D. $ -2$
E. $ -3$
$A(-1,1)$, $B(3; 3)$ цэгүүдийг дайрсан шулууны налалтыг олоорой.
A. $ -\dfrac12$
B. $ \dfrac{1}{2}$
C. $ 2$
D. $ -2$
E. $ -3$
Шулууны тэгшитгэл
$-4x-3y = 25$ шулуун дээр орших координатын эхээс хамгийн бага зайд байх цэгийн координатыг ол.
$x-2y=-5 \boldsymbol{\cdots}(1)$, $3x+2y=-7 \boldsymbol{\cdots}(2)$, $Rx-y=1-R \boldsymbol{\cdots}(3)$ шулуунууд өгөгдөв.
- Гурван шулуун нэг цэгт огтлолцох;
- Гурван шулууны огтлолцлын цэг хоёр байх;
- Гурван шулууны огтлолцлын цэг гурав байхаар $R$ тоог тус тус ол.
$(2k+3)x-(4k-1)y-16k-3=0$ шулуунуудын ерөнхий цэгийн координатыг ол.
$(a-2)x+ay+2=0, x+(a-2)y+1=0$ шулуунууд $a=\ebox$ үед параллель, $a=\ebox$
үед давхцаж, $a=\ebox$ үед перпендикуляр байна.
- $4x+3y-8=0$ ба $5y+3=0$ шулуунуудаар үүсэх өнцгүүдийн биссектрисийн тэгшитгэл бич.
- $x$ тэнхлэг, $y$ тэнхэг, $4x+3y=12$ шулуунуудаар хүрээлэгдсэн гурвалжинд багтсан тойргийн төвийг ол.
$y=3x+3$, $y=-2x+3$ шулуунуудын хоорондох хурц өнцгийг ол.
$x+y=1 \boldsymbol{\cdots}(1), 3x+4y=1 \boldsymbol{\cdots}(2), ax+by=1 \boldsymbol{\cdots}(3) $ шулуунууд нэг цэгт огтлолцдог бол $(1, 1)$, $(3, 4)$, $(a, b)$ цэгүүд нэг шулуун дээр оршино гэж батал.
- $P(2, 8)$ цэгээс дараах шулуунууд хүртэлх зайг ол.
- $3x-2y+4=0$;
- $x=-1$.
- $5x+4y=20$, $5x+4y=60$ шулуунуудын хоорондох зайг ол.
$A(0,-2)$, $B(4,0)$ цэгүүд ба $y=x^2$ парабол дээр хөдөлж буй $P$ цэгүүдээр
тодорхойлогдох $S_{\triangle PAB}$-ийн хамгийн бага утгыг ол.
Координатын эх дээр огтлолцсон, хоорондоо перпендикуляр $f$ ба $g$ шулуунууд өгөгджээ. I мужийг дайрах шулуун нь $f$ ба $OX$ тэнхлэгтэй $\theta$ өнцөг үүсгэнэ. Mөн $y=\dfrac{x}{\sqrt{3}}+a$ $(a>0)$ шулуун $f$, $g$, $OY$ шулуунуудыг харгалзан $P$, $Q$, $R$ цэгүүдээр огтолно. $PR=RQ$ байх $\theta$ өнцгийн утгыг ол.
Хавтгайд $O$ цэгт огтолцсон $\ell$, $m$ шулуунууд
өгөгдөв. $A_1, A_2, A_3\in \ell$, $B_1, B_2, B_3\in m$ байхаар $O$-той давхцахгүй зургаан цэгийн хувьд $A_1B_2\parallel A_2B_1$ ба $A_1B_3\parallel A_3B_1$ бол $A_2B_3\parallel A_3B_2$ болохыг харуул.
$B(-2,1)$ цэг ба $2x-y+1=0 \boldsymbol{\cdots}(1)$ ба $x+y-4=0 \boldsymbol{\cdots}(2)$
шулуунуудын огтлолцолыг дайрсан шулууны тэгшитгэлийг бич.
$x-\sqrt{3}y+1=0$, $x+\sqrt{3}y-2=0$ шулуунуудын хоорондох өнцгийг ол.
$A(3,-4)$, $B(1, 2)$, $l: 2x-3y+6=0$ байв. $A$ цэгийг дайрах $l$-шулуунтай
параллель болон перпендикуляр шулууны тэгшитгэлийг бич. Мөн $B$-г
дайрах $AB$-д перпендикуляр шулууны тэгшитгэлийг бич.
$2x+y+1=0$, $4x-ay+2=0$ шулуунуудын хоорондох өнцөг $45^{\circ}$
байх $a$-ийн утгыг ол.
$A(-1,-10)$, $B(2,-a)$, $C(a, 0)$ гурван цэг нэг шулуун дээр орших бол $a$-ийн утгыг ол.
Дараах шулуунууд огтлолцлын цэгтэй юу, огтлолцох бол огтлолцлын цэгийн координатыг ол.
- $\bigg\{% \begin{array}{cl} 2x-3y-14=0 & \boldsymbol{\cdots}(1)\\ 3x+4y-4=0 & \boldsymbol{\cdots}(2) \end{array}$
- $\bigg\{% \begin{array}{cl} 6x-9y+12=0 & \boldsymbol{\cdots}(3)\\ 6y-4x+12=0 & \boldsymbol{\cdots}(4) \end{array}$
- $\bigg\{% \begin{array}{cl} ax+4y+1=0 & \boldsymbol{\cdots}(5)\\ x+(a-3)y-1=0 & \boldsymbol{\cdots}(6) \end{array}$
- $\left(-\dfrac23, \dfrac52\right)$ цэгийг дайрсан $-\dfrac65$ өнцгийн коэффициенттэй шулууны тэгшитгэл бич.
- Дараах 2 цэгийг дайрсан шулууны тэгшитгэл бич.
- $(3,-5), (-7, 2)$
- $(3, 0), (0, 4)$
- $(2, 3), (-1, 3)$
$(1, 2)$ цэгийг дайрсан $2x-3y-4=0$ шулуунтэй параллель шулууны тэгшитгэл бич.
$A(1, 6), B(3, 1), C(5, 3)$ цэгүүд өгөгдөв.
- $C$-г дайрсан $AB$-тэй параллель шулууны тэгшитгэл бич.
- $AB$-ийн дунджыг дайрсан $AB$-д перпендикуляр шулууны тэгшитгэл бич.
$ax+2y=a, x+(a+1)y=a+3$ шулуунууд $a=\ebox$ үед параллель, $a=\ebox$ үед давхцаж, $a=\ebox$ үед перпендикуляр байна. Хэрэв эдгээр шулуунууд нэг цэгээр огтолцох бол огтлолцлын цэгийн координат нь $(x, y)=\ebox$.
$x$ тэнхлэгийн хувьд $3x-2y-6=0$ шулуунтэй тэгш хэмтэй шулууны тэгшитгэлийг бич.
- $y=2x+3$ шулууны хувьд $(3, 4)$ цэгтэй тэгш хэмтэй цэгийг ол.
- $y=2x+3$ шулууны хувьд $3x-2y-1=0$ шулуунтай тэгш хэмтэй шулууны тэгшитгэлийг бич.
Дараах шулуунууд огтлолцлын цэгтэй юу, огтлолцох бол огтлолцлын цэгийн координатыг ол.
- $\left\{% \begin{alignedat}{5} 7x & {}+{} & y & {}+{} & 18 &=0\\ 4x & {}-{} & 3y & {}-{} & 4 &=0 \end{alignedat}% \right.$
- $\left\{% \begin{alignedat}{5} 2x & {}+{} & 3y & {}-{} & 3 &=0\\ 4x & {}+{} & 6y & {}+{} & 6 &=0 \end{alignedat}% \right.$
- $\left\{% \begin{alignedat}{5} 3x & {}-{} & 4y & {}-{} & 1 &=0\\ 9x & {}-{} & 12y & {}-{} & 3 &=0 \end{alignedat}% \right.$
- $\left\{% \begin{alignedat}{5} ax & {}+{} & y &=10\\ x & {}+{} & ay &=1 \end{alignedat}% \right.$
$2x-y-1=0, x+5y-17=0$ шулуунуудын огтлолцлыг дайрсан $4x+3y-6=0$ шулуунтай параллель болон перпендикуляр шулууны тэгшитгэлийг бич.
$(2a+1)x-(a+3)y-(11a+18)=0$ багц шулууны ерөнхий цэгийг ол.
$2x+3y-19=0$, $5x-3y+5=0$, $8x-5y+9=0$ шулуунууд нэг цэгт огтлолцохыг батал.
$2x-3y=-4$, $x+2y=-5$, $x-Ry=1+R$ шулуунууд хэдэн цэгээр огтлолцохыг $R$ параметрээс хамааруулан тогтоо.
$A(-2,3)$, $B(1,2)$, $C(3t+4,-2t+2)$ цэгүүд нэг шулуун дээр орших $t$-г ол.
$x+3y=2a$, $3x+5y=2a$, $(a+1)x-ay=-1$ шулуунууд нэг цэгт огтлолцдог бол огтлолцлын цэг ба $a$-г ол.
$(1,1), (3,4), (a,b)$ цэгүүд нэг шулуун дээр орших бол $x+y=1$, $3x+4y=1$, $ax+by=1$ шулуунууд нэг цэгт огтлолцохыг батал.
$\sqrt{3}x-2y+2=0$, $3\sqrt{3}x+y-1=0$ хоёр шулууны хоорондох өнцгийг ол.
$OX$ тэнхлэгтэй цагийн зүүний эсрэг чиглэлд $30^\circ$ үүсгэх шулууны налалт аль нь вэ?
A. $0.5$
B. $1.5$
C. $\sqrt{2}$
D. $\dfrac{\sqrt{3}}2$
E. $\dfrac1{\sqrt{3}}$
$3x+4y=25$ шулууны налалтыг ол.
A. $3$
B. $-3$
C. $\dfrac{3}{4}$
D. $\dfrac{4}{3}$
E. $-\dfrac{3}{4}$
$A(3;5)$, $B(4;1)$ бол $AB$ шулуунтай параллел координатын эхийг дайрсан шулууны тэгшитгэл аль нь вэ?
A. $4x+y=0$
B. $4x-y=0$
C. $x+4y=0$
D. $x-4y=0$
E. $4x+y-17=0$
$x-2y-1=0$, $2x+y-7=0$ шулуунуудын огтлолцлын цэгийн координатыг ол.
A. $(5;2)$
B. $(3;1)$
C. $(2;3)$
D. Огтлолцохгүй
E. $(2;1)$
Координатын хоёр тэнхлэгээс ижил зайтай орших цэгүүдээс
тогтсон шулууны тэгшитгэл аль вэ?
A. $|x|=y$
B. $|y|=x$
C. $y=2x$
D. $x=2y$
E. $y=x$
Координатын $II$ ба $IV$ өнцгийн биссектрис шулууны
тэгшитгэл аль вэ?
A. $y=-2x$
B. $x-y=0$
C. $x+y=0$
D. $x+y+1=0$
E. Аль нь ч биш
$2x-y-b=0$ шулуун $M(3;1)$ цэгийг дайрах $b$-ийн утга аль
вэ?
A. $6$
B. $-6$
C. $5$
D. $-5$
E. $0$
$x-2y-c=0$ шулуун $N(5;1)$ цэгийг дайрах $c$-ийн утга аль
вэ?
A. $6$
B. $3$
C. $-6$
D. $-3$
E. $0$
$x-2y-5=0$ шулуун дээр орших цэгийг заа.
A. $(5;1)$
B. $(3;-2)$
C. $(1;-2)$
D. $(1;5)$
E. $(5,5)$
$2x-y+3=0$ шулуун дээр үл орших цэгийг заа.
A. $(2,7)$
B. $(2,1)$
C. $(-2,-1)$
D. $(-1,1)$
E. $(0,3)$
$\alpha x+\beta y=1$ шулуун $(2;1)$, $(0;-1)$ хоёр цэгийг дайрах
$(\alpha;\beta)$ аль вэ?
A. $(1;1)$
B. $(-1;-1)$
C. $(-1;1)$
D. $(1;-1)$
E. $(1;0)$
$\alpha x+\beta y=1$ шулуун $(1;2)$, $(0;1)$ хоёр цэгийг дайрах
$(\alpha;\beta)$ аль вэ?
A. $(1;1)$
B. $(1;-1)$
C. $(-1;1)$
D. $(-1;-1)$
E. $(1;0)$
$(-1;1)$ цэгийг дайрсан шулуун абсцисс тэнхлэгийн эерэг чиглэлтэй $45^\circ$ өнцөг үүсгэсэн бол тэгшитгэл нь аль вэ?
A. $x+y+2=0$
B. $x-y+2=0$
C. $x+y-2=0$
D. $x-y-2=0$
E. $y=x$
$(-1;-1)$ цэгээр дайрсан шулуун ординат тэнхлэгийн эерэг чиглэлтэй $45^\circ$ өнцөг үүсгэсэн бол тэгшитгэл нь аль вэ?
A. $x+y+2=0$
B. $x-y+2=0$
C. $x+y-2=0$
D. $x-y-2=0$
E. $x-y=0$
$x-1.5=0$ шулуунтай ординат тэнхлэгийн хувьд тэгш хэмтэй
орших шулууны тэгшитгэл аль вэ?
A. $x=1.5$
B. $x=y$
C. $x=-1.5$
D. $x+1.5=y$
E. $y-1.5=0$
$y+2=0$ шулуунтай абсцисс тэнхлэгийн хувьд тэгш хэмтэй орших
шулууны тэгшитгэл аль вэ?
A. $y=x+2$
B. $y=-2$
C. $x+2=0$
D. $y-2=0$
$x+my=1$ шулуун $(-1,1)$ цэгээр дайрах $m$-ийн утга аль вэ?
A. $3$
B. $2.1$
C. $2$
D. $-2$
E. $-3$
$kx+2y=3$ шулуун $(3;3)$ цэгээр дайрах $k$-ийн утга аль вэ?
A. $1$
B. $2$
C. $-2$
D. $-1$
$x-ky-3=0$ шулуун $x+y-5=0$ шулуунтай параллель байх $k$-ийн
утга аль вэ?
A. $1$
B. $\frac12$
C. $-1$
D. $-\frac12$
$kx-2y+6=0$ шулуун $2x+y-1=0$ шулуунтай параллель байх
$k$-ийн утга аль вэ?
A. $\frac12$
B. $-\frac12$
C. $2$
D. $-4$
E. $-2$
$M(3;1)$, $N(1;3)$. $MN$ хэрчмийн дундажаар дайрсан шулууны
тэгшитгэл аль вэ?
A. $x-2y=2$
B. $2x+y=5$
C. $2x-y=2$
D. $x+2y=5$
$M(3;-1)$, $N(-3;1)$. $MN$ хэрчмийн дундажаар дайрсан
шулууны тэгшитгэл аль вэ?
A. $x+2y=2$
B. $x+y=1$
C. $x+2y=0$
D. $x-2y=2$
$3x+4y-7=0$ шулуунтай пердендикуляр шулууны өнцгийн коэффициент аль нь вэ?
A. $-1$
B. $\dfrac34$
C. $\dfrac43$
D. $-\dfrac34$
E. $-\dfrac43$
Зурагт дүрслэгдсэн шулууны өнцгийн коэффициентийг ол.
%

A. $\sqrt3$
B. 120
C. 1
D. $\dfrac{\sqrt3}{3}$
E. 60
$A(3,4)$, $B(-2,3)$ цэгүүдийг дайрсан шулууны тэгшитгэл аль нь вэ?
A. $x+5y-23=0$
B. $x+5y-13=0$
C. $x-5y+17=0$
D. $5x+y-19=0$
E. $x+y-7=0$
$2x-3y=5$ шулуунд перпендикуляр байх шулуун аль нь вэ?
A. $-2x+3y=5$
B. $2x-3y=5$
C. $3x+2y=5$
D. $-3x+2y=5$
E. $2x+3y=-5$
$x+y=-2$ шулуун аль нь вэ?


A. 1)
B. 2)
C. 3)
D. 4)
E. 5)
$y=4x+5$ шулуунтай аль шулуун нь огтлолцохгүй вэ?
A. $y=\dfrac14x-5$
B. $y=-\dfrac14x-5$
C. $y=4x+\dfrac15$
D. $y=-4x+\dfrac15$
E. $y=-4x-5$
$2x+3y=5$ шулуунд перпендикуляр байх шулуун аль нь вэ?
A. $-2x+3y=5$
B. $2x-3y=5$
C. $3x+2y=5$
D. $-3x+2y=5$
E. $2x+3y=-5$
$3x+y-4=0$ шулуунтай пердендикуляр $A(3,2)$ цэгийг дайрсан шулууны тэгшитгэл аль нь вэ?
A. $x-3y-3=0$
B. $3x+y-11=0$
C. $x+3y-9=0$
D. $x-3y+3=0$
E. $x+3y=0$
$2x+3y-5=0$ шулуунтай пердендикуляр $A(2;3)$ цэгийг дайрсан шулууны тэгшитгэл аль нь вэ?
A. $3x+2y-12=0$
B. $3x-2y=0$
C. $3x-2y-12=0$
D. $2x+3y-13=0$
E. $2x+3y=0$
$2x+3y-5=0$ шулуунтай параллель $A(2;3)$ цэгийг дайрсан шулууны тэгшитгэл аль нь вэ?
A. $3x+2y-12=0$
B. $3x-2y=0$
C. $3x-2y-12=0$
D. $2x+3y-13=0$
E. $2x+3y=0$
$A(2,3)$, $B(-2,-4)$ бол $AB$ шулууны тэгшитгэл аль нь вэ?
A. $2x+3y=0$
B. $4x+7y=29$
C. $7x-4y=2$
D. $4x-7y=-20$
E. $7x-4y=0$
$A(2;-3)$, $B(-2;4)$ бол $AB$ шулууны тэгшитгэл аль нь вэ?
A. $2x-3y=0$
B. $4x-7y+29=0$
C. $7x+4y-2=0$
D. $4x+7y-20=0$
E. $7x+4y=0$
$A(1,2)$; $B(4,3)$ цэгүүдийг дайрсан шулууны тэгшитгэл аль нь вэ?
A. $\begin{vmatrix} x-1 & y-2\\ 4 & 3 \end{vmatrix}=0$
B. $\begin{vmatrix} x+1 & y+2\\ 5 & 5 \end{vmatrix}=0$
C. $\begin{vmatrix} x-1 & y-2\\ 1 & 2 \end{vmatrix}=0$
D. $\begin{vmatrix} x+1 & y+2\\ 3 & 1 \end{vmatrix}=0$
E. $\begin{vmatrix} x-1 & y-2\\ 3 & 1 \end{vmatrix}=0$
$A(1,2,3)$, $B(-2,0,1)$ цэгүүдийг дайрсан шулууны вектор тэгшитгэлийг бич.
A. $\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}1\\2\\3\end{pmatrix}+t\begin{pmatrix}-3\\-2\\-2\end{pmatrix}$
B. $\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}1\\2\\3\end{pmatrix}+t\begin{pmatrix}-2\\ \phantom{-}0\\ \phantom{-}1\end{pmatrix}$
C. $\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}-2\\ \phantom{-}0\\ \phantom{-}1\end{pmatrix}+t\begin{pmatrix}1\\2\\3\end{pmatrix}$
D. $\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}-3\\-2\\-2\end{pmatrix}+t\begin{pmatrix}1\\2\\3\end{pmatrix}$
E. $\begin{pmatrix}x\\y\\z\end{pmatrix}=t\begin{pmatrix}3\\2\\2\end{pmatrix}-\begin{pmatrix}1\\2\\3\end{pmatrix}$
$\boldsymbol{r}=(3,8-2)+t(2,-1,3)$ ба $\boldsymbol{r}=(7,4,3)+s(2,1,4)$ хоёр шулууны харилцан байршлыг тодорхойл.
A. Параллел
B. $(9,5,-7)$ цэгт огтлолцоно
C. Давхцсан
D. Зөвхөн $(9,5,7)$ цэгт огтлолцоно
E. Координатын эх дээр огтлолцоно
$\boldsymbol{r}=(2,1,0)+t(1,2,3)$ ба $\boldsymbol{r}=(4,5,6)+s(2,4,6)$ хоёр шулууны харилцан байршлыг тодорхойл.
A. Параллел
B. Давхцсан
C. Солбисон
D. Зөвхөн $(2,1,0)$ цэгт огтлолцоно
E. $(1,2,3)$ цэгт огтлолцоно
$\boldsymbol{r}=(2,0,1)+t(-3,3,3)$ ба $\boldsymbol{r}=(1,3,0)+s(1,-1,1)$ хоёр шулууны харилцан байршлыг тодорхойл.
A. Зөвхөн $(-1,3,4)$ цэгт огтлолцоно
B. Давхцсан
C. Солбисон
D. Параллел
E. $(1,3,0)$ цэгт огтлолцоно
$\boldsymbol{r}=(2,8,0)+t(2,3,-1)$ ба $\boldsymbol{r}=(0,1,10)+s(-2,-3,1)$ хоёр шулууны харилцан байршлыг тодорхойл.
A. Параллел
B. Давхцсан
C. Солбисон
D. Зөвхөн $(6,6,6)$ цэгт огтлолцоно
E. $(1,2,3)$ цэгт огтлолцоно
$\boldsymbol{r}=(1,3-2)+t(1,4,9)$ ба $\boldsymbol{r}=(3,-1,2)+s(4,9,1)$ хоёр шулууны хоорондох өнцгийг ол.
A. $0^\circ$
B. $30^\circ$
C. $45^\circ$
D. $60^\circ$
E. $75^\circ$
Зурагт өгөгдсөн A дүрсийг B дүрсэд хувиргажээ. Хувиргалтын матрицыг олоорой.
A. $\begin{pmatrix} 0 & -1 \\ -1 &0 \end{pmatrix}$
B. $\begin{pmatrix} 0& -1 \\ 1 &0 \end{pmatrix}$
C. $\begin{pmatrix} 1& 0 \\ 0 &-1 \end{pmatrix}$
D. $\begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}$
E. $\begin{pmatrix} -1 & 0 \\ 0 &1 \end{pmatrix}$
$y=3x+1$ шулуунтай перпендикуляр бөгөөд координатын эхийг дайрсан шулууны тэгшитгэлийг бичээрэй.
A. $y=-3x$
B. $y=3x$
C. $y=\dfrac13x$
D. $y=\dfrac13x+1$
E. $y=-\dfrac13x$
$ABCD$ параллелограммын $AB$ тал $y=3x+1$ тэгшитгэлтэй, $AD$ тал $4y=x+15$ тэгшитгэлтэй. $AC$ ба $BD$ диагоналиуд нь $E(6.5,7.5)$ цэгт огтлолцдог бол $C$ цэгийн координатыг олоорой.

A. $(8;10)$
B. $(1;3)$
C. $(6;8)$
D. $(13;15)$
E. $(12;11)$
$3x+2y-5=0$ шулуунтай перпендикуляр бөгөөд координатын эхийг дайрсан шулууны тэгшитгэлийг бичээрэй.
A. $y=-3x$
B. $y=-\dfrac23x$
C. $y=\dfrac23x$
D. $y=\dfrac13x+1$
E. $y=\dfrac32x$
$y=2x+5$ шулуунтай перпендикуляр бөгөөд координатын эхийг дайрсан шулууны тэгшитгэлийг бичээрэй.
A. $y=\dfrac12x$
B. $y=-2x$
C. $y=-\dfrac12x$
D. $y=\dfrac12x+1$
E. $y=2x$
$ABCD$ параллелограммын $AB$ тал $y=3x+1$ тэгшитгэлтэй, $AD$ тал $4y=x+15$ тэгшитгэлтэй. $AC$ ба $BD$ диагоналиуд нь $E(6.5,7.5)$ цэгт огтлолцдог бол $C$ цэгийн координатыг олоорой.

A. $(13;17)$
B. $(1;3)$
C. $(6;8)$
D. $(12;14)$
E. $(8;10)$
$ 2y - x-2 = 0$, $y +2x -6 = 0$, $y = 0$ тэгшитгэлтэй шулуунуудын огтлолцолд үүсэх гурвалжны талбайн хэмжээг олоорой.
A. $6$ нэгж.кв
B. $10$ нэгж.кв
C. $2.5$ нэгж.кв
D. $6$ нэгж.кв
E. $8$ нэгж.кв
8. $ A(1,1,6) $, $В(1, 2, 7) $, $C ( 3, 3, 6) $ , $D (5, 2, 6)$ цэгүүд өгөгдсөн бол
a. $ AB $ , $ CD $ шулуунууд ямар байрлалтай болохыг тодорхойл.
б. $ AC $, $ BD $ шулуунуудын хоорондох өнцгийг ол.
a. $ AB $ , $ CD $ шулуунууд ямар байрлалтай болохыг тодорхойл.
б. $ AC $, $ BD $ шулуунуудын хоорондох өнцгийг ол.
$y = \dfrac{1}{2}x-2 = 0$, $y +2x +2 = 0$, $y = 0$ тэгшитгэлтэй шулуунуудын огтлолцолд үүсэх гурвалжны талбайн хэмжээг олоорой.
A. $10$ нэгж.кв
B. $5$ нэгж.кв
C. $2.5$ нэгж.кв
D. $6$ нэгж.кв
E. $8$ нэгж.кв
$ y - \frac{1}{2}x-3 = 0$, $ y +2x+2 = 0 $, $y = 0$ тэгшитгэлтэй шулуунуудын огтлолцолд үүсэх гурвалжны талбайн хэмжээг олоорой.
A. $10$ нэгж.кв
B. $5$ нэгж.кв
C. $2.5$ нэгж.кв
D. $6$ нэгж.кв
E. $8$ нэгж.кв
$A(2,3)$, $B(-2,-4)$ бол $AB$ шулууны тэгшитгэл аль нь вэ?
A. $2x+3y=0$
B. $4x+7y=29$
C. $7x-4y=2$
D. $4x-7y=-20$
E. $7x-4y=0$
$A(1,1), B(-3,4), C(3,2)$ цэгүүд өгөв.
- $AB$ хэрчмийн урт $\fbox{a}$ байна.
- $AB$ шулууны тэгшитгэл $\fbox{b}x+\fbox{c}y-\fbox{d}=0$ байна.
- $C$ цэгээс $AB$ шулуун хүртэлх зай $\fbox{e}$ болно.
- $ABC$ гурвалжны талбай $\fbox{f}$ байна.
$A(1;1)$, $B(2;3)$, $C(4;-2)$ цэгүүд өгөгдөв. $AB$ хэрчмийн урт $\sqrt{\fbox{a}}$, $AB$ шулууны тэгшитгэл $\fbox{b}x-\fbox{c}y-1=0$ байна. $C$ цэгээс $AB$ шулуун хүртэлх зай $\dfrac{\fbox{d}}{\sqrt{\fbox{e}}}$ бөгөөд $ABC$ гурвалжны талбай нь $\dfrac{\fbox{f}}{\fbox{g}}$ байна.
Дараах нөхцөлийг хангах шулууны тэгшитгэлийг бич.
- $(-1,3)$ цэгийг дайрсан $-2$ өнцгийн коэффициенттэй шулуун $y=-2x+\fbox{a}$;
- $(1,-2)$ ба $(-3,4)$ цэгүүдийг дайрсан шулуун $\fbox{b}x+\fbox{c}y+1=0$;
- $(4,1)$ ба $(4,5)$ цэгүүдийг дайрсан шулуун $x=\fbox{d}$;
- $(4,0)$ цэгийг дайрсан $4x-5y+3=0$ шулуунтай перпендикуляр шулуун $y=-\dfrac{\fbox{e}}{\fbox{f}}x+\fbox{g}$.
$A(1;0)$, $B(4;4)$ бол $\overrightarrow{AB}=(\fbox{a},\fbox{b})$ байна. $AB$ хэрчмийн дундач цэгийн координат нь $C\Big(\dfrac{\fbox{c}}{2};\fbox{d}\Big)$ байна. $C$ цэгийг дайрсан $AB$-д перпендикуляр шулууны тэгшитгэл нь $\fbox{ef}x+\fbox{g}y-33=0$ байна.
$y=\dfrac{x-2}{x-1}$ функц өгөгдөв.
- $y=\dfrac{x-2}{x-1}$ функцийн $x_0=2$ цэгт татсан шүргэгч шулууны тэгшитгэлийг бичвэл $y=\fbox{a}x-\fbox{b}$;
- $y=\dfrac{x-2}{x-1}$, $x=2$, $x=5$ ба $y=0$ шугамуудаар хүрээлэгдсэн дүрсийн талбай $\fbox{c}-\ln\fbox{d}$;
- $y=5x+5$ шулуунд перпендикулар ба $(1;1)$ цэгийг дайрсан шулууны тэгшитгэл нь $\fbox{e}x+\fbox{f}y-6=0$;
- $y=\dfrac{x-2}{x-1}$ муруй ба $x-3y-2=0$ шулууны огтлолцлын цэгүүдийн хоорондох зай $\dfrac{2}{3}\sqrt{\fbox{gh}}$.
$y=\dfrac{x}{x-1}$ функц өгөгдөв.
- $y=\dfrac{x}{x-1}$ функцийн $x_0=2$ цэгт татсан шүргэгч шулууны тэгшитгэлийг бичвэл $y=-\fbox{a}x+\fbox{b}$
- $y=\dfrac{x}{x-1}$, $x=2$, $x=4$ ба $y=0$ шугамуудаар хүрээлэгдсэн дүрсийн талбай $\fbox{c}+\ln\fbox{d}$
- $y=2x+5$ шулуунд перпендикуляр ба $(1;1)$ цэгийг дайрсан шулууны тэгшитгэл нь $\fbox{e}x+\fbox{f}y-3=0$.
- $y=\dfrac{x}{x-1}$ функц ба $x+5y-12=0$ шулууны огтлолцлын цэгүүдийн хоорондох зай $\dfrac45\sqrt{\fbox{gh}}$
$y=\dfrac{x}{x-1}$ функц өгөгдөв.
- $y=\dfrac{x}{x-1}$ функцийн $x_0=0$ цэгт татсан шүргэгч шулууны тэгшитгэлийг бичвэл $y=-\fbox{a}x+\fbox{b}$;
- $y=\dfrac{x}{x-1}$, $x=2$, $x=5$ ба $y=0$ шугамуудаар хүрээлэгдсэн дүрсийн талбай $\fbox{c}+\ln\fbox{d}$;
- $y=3x+5$ шулуунд перпендикулар ба $(1;1)$ цэгийг дайрсан шулууны тэгшитгэл нь $\fbox{e}x+\fbox{f}y-4=0$;
- $y=\dfrac{x}{x-1}$ муруй ба $x+4y-10=0$ шулууны огтлолцлын цэгүүдийн хоорондох зай $\dfrac{3}{4}\sqrt{\fbox{gh}}$.
$y=\dfrac{x-2}{x-1}$ функц өгөгдөв.
- $y=\dfrac{x-2}{x-1}$ функцийн $x_0=0$ цэгт татсан шүргэгч шулууны тэгшитгэлийг бичвэл $y=\fbox{a}x+\fbox{b}$;
- $y=\dfrac{x-2}{x-1}$, $x=2$, $x=4$ ба $y=0$ шугамуудаар хүрээлэгдсэн дүрсийн талбай $\fbox{c}-\ln\fbox{d}$;
- $y=4x+5$ шулуунд перпендикулар ба $(1;1)$ цэгийг дайрсан шулууны тэгшитгэл нь $\fbox{e}x+\fbox{f}y-5=0$;
- $y=\dfrac{x-2}{x-1}$ муруй ба $x-3y+6=0$ шулууны огтлолцлын цэгүүдийн хоорондох зай $\dfrac23\sqrt{\fbox{gh}}$.
Зургаас дараах функцийн $a,b,c,d,e,f,g$-г ол.
$$f(x)=\left\{\begin{array}{lll}\fbox{ab}, & x\le-2 & (2\text{ оноо)}\\ \fbox{c}\cdot x+\fbox{d}, & -2< x\le -1 & (2\text{ оноо)}\\ \fbox{e}\cdot x+\fbox{f}, & -1< x\le 0 & (2\text{ оноо)}\\ \fbox{g}, & x>0 & (1\text{ оноо)}\end{array}\right.$$
$$f(x)=\left\{\begin{array}{lll}\fbox{ab}, & x\le-2 & (2\text{ оноо)}\\ \fbox{c}\cdot x+\fbox{d}, & -2< x\le -1 & (2\text{ оноо)}\\ \fbox{e}\cdot x+\fbox{f}, & -1< x\le 0 & (2\text{ оноо)}\\ \fbox{g}, & x>0 & (1\text{ оноо)}\end{array}\right.$$

$\ell_1\colon 3x+4y+5=0$ шулуун ба $\ell_2\colon 9x+\fbox{ab}y-30=0$ шулуунууд параллель бол координатын эхээс
$\ell_1$ хүртэлх зай $\fbox{c}$, $\ell_2$ хүртэлх зай $\fbox{d}$; $\ell_1$ ба $\ell_2$ шулуунуудын хоорондох зай нь $\fbox{e}$ байна.
$\ell\colon y=px-3\ (p>0)$, $m\colon y=\dfrac12x+2$ шулуунуудын огтлолцолын цэгийг $C$, $x$ тэнхлэгтэй огтлолцох цэгүүдийг нь $A$, $B$ гэе. $S_{ABC}=\dfrac{15}{2}$ бол $p=\fbox{a}$ байна. Энэ үед $\ell$, $m$ шулуунуудын $x$ тэнхлэгтэй үүсгэх өнцгийг $\alpha$, $\beta$ гэвэл $\tg\alpha=\fbox{b}$, $\tg\beta=\dfrac{\fbox{c}}{\fbox{d}}$ болно. Иймд эдгээр шулуунуудын хоорондох хурц өнцөг $\gamma=\dfrac{\pi}{\fbox{e}}$ байна.
$A(3,2)$ цэгийг дайрсан $\ell\colon x+3y-5=0$ шулуунтай параллель шулууны тэгшитгэл $y=-\dfrac{1}{\fbox{a}}x+\fbox{b}$, перпендикуляр шулуун тэгшитгэл $y=\fbox{c}x-\fbox{d}$ байна.
$A(1,1), B(4,-3), C(2,3)$ цэгүүд өгөв.
- $AB$ хэрчмийн урт $\fbox{a}$ байна.
- $AB$ шулууны тэгшитгэл $\fbox{b}x+\fbox{c}y-\fbox{d}=0$ байна.
- $C$ цэгээс $AB$ шулуун хүртэлх зай $\fbox{e}$ болно.
- $ABC$ гурвалжны талбай $\fbox{f}$ байна.