KöMaL, B ангилал, 2018 оны 9-р сар   

1. Цифрүүдийн нийлбэр нь 2018-тай тэнцүү арван найм дахь натурал тоог ол.

(3 оноо)

2. $P$ нь $\triangle ABC$-ийн дотоод цэг ба $C_1$, $A_1$ and $B_1$ нь харгазан $AB$, $BC$, $CA$ талуудын дундаж цэг байв. $A_1$, $B_1$, $C_1$ цэгүүдийг дайруулж $AP$, $BP$, $CP$ шулуунуудтай харгалзан параллел байх шулуунууд татав. Эдгээр шулуунууд нэг цэгт огтлолцохыг харуул.

Дэвшүүлсэн J. Kozma, Szeged

(3 оноо)

3. Дараах нөхцөлүүдийг зэрэг хангах эерэг бодит тоонуудыг ол: \begin{align*} \dfrac{1}{1+a+ab+abc}+\dfrac{1}{1+b+bc+bcd}+\dfrac{1}{1+c+cd+cda}+\dfrac{1}{1+d+da+dab}=1\\ a+b+c+d=4 \end{align*} (4 оноо)

4. $T$ тэгш өнцөгтийн талууд нь $a\le b$. Хэрвээ $r$ радиустай 2 дугуйгаар $T$ тэгш өнцөгтийг хучиж болдог, $r$-ээс бага радиустай 2 дугуйгаар хучиж болдоггүй бол $r$-ийг ол.

(4 оноо)

5. $A$, $B$ цэгүүд $e$ шулууны хоёр талд байрладаг. $e$ шулуун дээр $\angle PAQ=90^\circ$ байхаар $P$, $Q$ цэгүүдийг сонгов. $P$, $Q$ цэгүүдийн сонголтоос үл хамааран $BPQ$ гурвалжныг багтаасан тойрог дээр орших $B$-ээс ялгаатай цэг оршин байна гэж батал.

Дэвшүүлсэн Fazekas сургуулийн 11С анги

(5 оноо)

6. Ямар $p$ анхны тооны хувьд $1+a+a^2+\cdots+a^{p-1}$ тоо $p^2$-д хуваагдах вэ?

(5 оноо)

7. $ABC$ хурц өнцөгт гурвалжны дотор $P$ цэг өгөгджээ. $D$, $E$, $F$ нь $P$ цэгээс сууриуд руу перпендикуляр татав. Гурвалжны гадна талд талууд дээр үүсэх зургаан хэрчмээр талаа хийсэн квадратууд байгуулав. Тэдгээрийг зурагт үзүүлсний дагуу хоёр өнгөөр сөөлжилж буджээ. Ижил өнгийн квадратуудын гадна талуудаар үүсэх гурвалжнууд тэнцүү гэж батал.

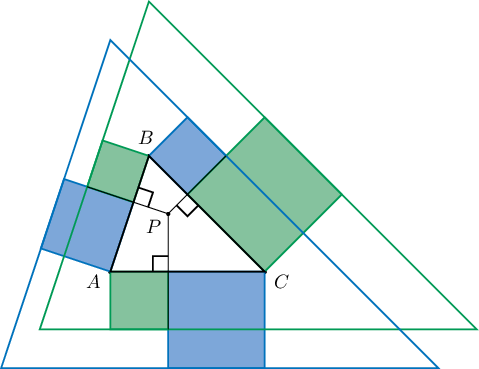
(6 оноо)

8. $a_1,a_2,\dots,a_{2018}$ сөрөг биш бодит тоонуудын нийлбэр 1-тэй тэнцүү. $S=\sum\limits_{i\neq j, i|j} a_i a_j$ илэрхийллийн боломжит хамгийн их утгыг ол.

Аргентиний бодлого

(6 оноо)