Хот хоорондын 40-р уралдаан, Намрын уралдаан, бэлтгэл даваа, IX-X анги, 10-р анги
Бодлогын тоо: 5 Хугацаа: 240 мин
1. Тэгш өнцөгт $ABC$ гурвалжны тэгш өнцгийн $B$ орой ба $AC$ гипотенузын дундаж цэгийг дайрсан тойрог гурвалжны хоёр катетыг $M$, $N$ цэгүүдэд огтлоно. $AC=2\cdot MN$ бол $M$, $N$ цэгүүд нь катетуудын дундаж цэгүүд гэдгийг батал.
(4 оноо)
(4 оноо)
2. $1,2,3,\dots,2n$ тоонуудыг $2$, $2$-оор нь хос болгон хувааж, хос тус бүрийн $2$ тооны нийлбэрийг боджээ. Ямар натурал $n$ тооны хувьд олсон бүх нийлбэрүүдийн үржвэр нь бүтэн квадрат тоо гарч болох вэ?
(4 оноо)
(4 оноо)
3. $7\times 14$ хэмжээтэй тэгш өнцөгтийг $2\times 2$ хэмжээтэй квадратууд ба 3 нүдтэй булан дүрсүүдэд хуваажээ (булан дүрсийг яаж ч эргүүлж болно).
- Хуваалтын квадратын тоо нь булан дүрсийн тоотой тэнцүү байж болох уу? (1 оноо)
- Хуваалтын квадратын тоо нь булан дүрсийн тооноос их байж болох уу? (3 оноо)
4. Цэцэгт харахад ижил 5 ширхэг зоос, Батад туухайгүй 2 тавагтай жинлүүр байв. Зооснуудын 3 нь жинхэнэ, 2 нь хуурамч байсан бөгөөд жинхэнэ зооснууд ижил жинтэй, харин хуурамч зооснуудын нэг нь жинхэнэ зоосноос хөнгөн, нөгөө нь жинхэнэ зоосноос хүнд жинтэй байжээ. Цэцэг зоос жинлэх 3 хүсэлтээ Батад бичиж өгнө. Бат жинлүүр дээр түүний хүссэн 3 жинлэлтийг жинлээд, харин үр дүнг нь зөвхөн бүх жинлэлтийг хийж дууссаны дараа хэлж өгдөг байв. Аль зоос нь хөнгөн, аль зоос нь хүнд хуурамч зоос вэ? гэдгийг мэдэж авч болохоор Цэцэг хүсэлтээ бичиж өгч чадах уу?
(5 оноо)
(5 оноо)
Заавар Бодолт
Заавар. Зооснуудаа $A$, $B$, $C$, $D$, $E$ гэвэл зооснуудаа хоёр, хоёроор нь жинлэх эсвэл $A+B$, $C+D$ гэсэн дөрвөн зоос жинлэх гэсэн 2 төрлийн захиалга өгөх боломжтой.
Бодолт. Зооснуудыг 2, 2-оор нь жинлээд хүнд, хөнгөн хуурамч зоосыг тодорхойлох боломжгүй гэдгийг харуулъя. Жинлэх зооснуудаа хэрчмээр холбоё. Тэгвэл дараах 3 тохиолдлын аль нэг нь үүснэ.
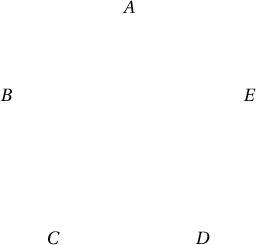 захиалга өгсөн үед $B < A$, $B < C$, $C = D$ гэсэн хариулт ирсэн үед $E$ зоос хуурамч жинхэнэ эсэхийг тодорхойлох боломжгүй.
захиалга өгсөн үед $B < A$, $B < C$, $C = D$ гэсэн хариулт ирсэн үед $E$ зоос хуурамч жинхэнэ эсэхийг тодорхойлох боломжгүй.
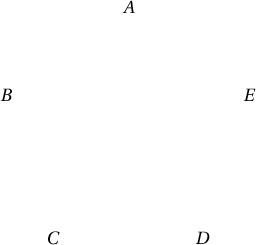 захиалга өгсөн үед $B < A$, $B < C$, $B < D$ гэсэн хариулт ирсэн үед $E$ зоос хуурамч жинхэнэ эсэхийг тодорхойлох боломжгүй.
захиалга өгсөн үед $B < A$, $B < C$, $B < D$ гэсэн хариулт ирсэн үед $E$ зоос хуурамч жинхэнэ эсэхийг тодорхойлох боломжгүй.
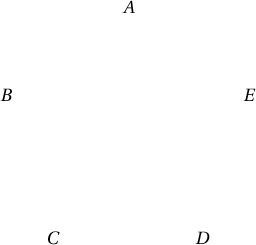 захиалга өгсөн үед $B < A$, $B < C$, $D = E$ гэсэн хариулт ирсэн үед $A$, $C$ зооснуудын аль нь хүнд хуурамч зоос гэдгийг тодорхойлох боломжгүй.
захиалга өгсөн үед $B < A$, $B < C$, $D = E$ гэсэн хариулт ирсэн үед $A$, $C$ зооснуудын аль нь хүнд хуурамч зоос гэдгийг тодорхойлох боломжгүй.
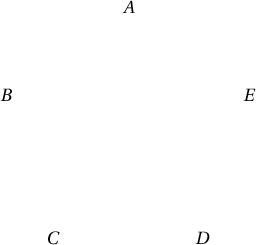 захиалга өгсөн үед $A=B=C$ гэсэн хариулт ирсэн үед $D$, $E$ зооснууд хуурамч боловч аль нь хүнд хуурамч зоос, аль нь хөнгөн хуурамч гэдгийг тодорхойлох боломжгүй.
захиалга өгсөн үед $A=B=C$ гэсэн хариулт ирсэн үед $D$, $E$ зооснууд хуурамч боловч аль нь хүнд хуурамч зоос, аль нь хөнгөн хуурамч гэдгийг тодорхойлох боломжгүй.
Одоо 4 зоос жинлэх $A+B$ ба $C+D$ гэсэн яг нэг захиалга өгсөн гэе.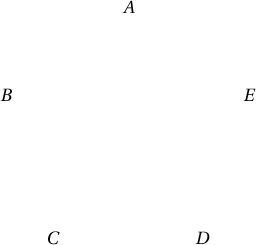




Одоо 4 зоос жинлэх $A+B$ ба $C+D$ гэсэн яг нэг захиалга өгсөн гэе.

5. Цифр бүр нь ялгаатай есөн оронтой тоог сайн тоо гэж нэрлэе. 37-д хуваагддаг сайн тоонууд 1000-аас цөөнгүй олдохыг харуул.
(5 оноо)
(5 оноо)