Хот хоорондын 40-р уралдаан, Намрын уралдаан, үндсэн даваа, VI-VIII анги, 8-р анги
Бодлогын тоо: 7 Хугацаа: мин
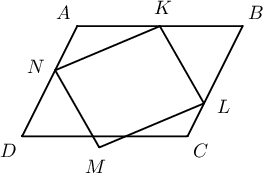
1. $KLMN$ параллелограммын $K$, $L$, $N$ оройнууд $ABCD$ параллелограммын харгалзан $AB$, $BC$, $DA$ талууд дээр оршино. $AK=KB$ бол $KM$ хэрчим нь $ABCD$ параллелограммын диагоналын огтлолцлын цэгийг дайрахыг батал.

2. $100\times100$ хэмжээтэй квадрат дотор шугамын дагуу 10000 ширхэг нэгж урттай хэрчим татаж, квадратыг 4 нүдтэй дүрсүүдэд хуваажээ. Хуваалтын дүрсүүд дотор $2\times 2$ хэмжээтэй хэдэн квадрат байсан бэ? Боломжит бүх хариуг олж, өөр хариу байхгүйг батал.
3. Нэгэн арал дээр 2018 хүн амьдардаг бөгөөд хүмүүсийн зарим нь үнэнч, зарим нь худалч, үлдсэн нь аялдан дагагч байсан бөгөөд хүн бүр бусдынхаа хэн нь хэн бэ? гэдгийг мэддэг байв. Арлын бүх суугчдыг нэг эгнээнд зогсоогоод Арлын үнэнч хүмүүс олон уу? гэсэн асуултыг хүн бүрээс ээлжлэн асуужээ. Хүн бүр тийм эсвэл үгүй гэсэн хариултыг хэлсэн бөгөөд үнэнч нь үнэн, худалч нь худал, харин аялдан дагагч нар түүнээс өмнө хариулсан хүмүүсийн олонхитой ижил хариултыг хэлнэ (хэрэв түүнээс өмнөх тийм, үгүй гэсэн хариулт тэнцвэл, ямар ч хамаагүй хариултыг хэлнэ.) Тийм гэсэх хариултын тоо яг $1009$ байсан бол арал дээр хамгийн олондоо хэдэн аялдан дагагч байсан бэ?
4. $77\ldots7$ хэлбэртэй тоонуудыг зөвхөн $7$ цифр ашиглан, нэмэх, хасах, үржих, хуваах, зэрэг дэвшүүлэх үйлдлийн тусламжтайгаар илэрхийлж болжээ (хаалт ашиглаж болох ба $7$ цифрүүдээ дангаар нь эсвэл $77$, $777$, $\ldots$ гэх мэтчилэн дараалж бичиж ашиглаж болно). Мэдээж нэг илэрхийлэл нь ердөө $77\ldots7$ гэж бичих явдал бөгөөд $77$-г хамгийн цөөн $7$ ашиглан ингэж бичих бичлэг нь $77$ юм. Аравтын бичлэгээс нь өөр цөөн тооны $7$ цифр ашиглан бичиж болдог $77\ldots7$ хэлбэртэй тоо олдох уу?
5. $10\times 10$ хэмжээтэй хөлгөөс $1\times 2$ хэмжээтэй тэгш өнцөгт үүсгэх 2 нүдийг ухаж авчээ. Хөлгийн үлдсэн хэсгийг зурагт үзүүлсэн хоёр төрлийн дүрсэд хувааж болох уу?


6. $7\times7$ хэмжээтэй хөлөг дээр шугамын дагуу талуудтай $2\times2$ хэмжээтэй квадрат үүсгэх үл харагдах онгоц байрлана эсвэл хөлөг онгоц хоосон байна. Хөлгийн зарим нүдэн онгоц илрүүлэгч байрлуулаад, байрлуулсан илрүүлэгчдээ нэгэн зэрэг ажиллуулж болно. Хэрэв илрүүлэгчтэй нүдэнд онгоц байвал тэр илрүүлэгч дохио өгнө. Онгоцны байрлалыг, мөн хөлөг онгоц хоосон эсэхийг мэдэхийн тулд хөлөг дээр хамгийн цөөндөө хэдэн илрүүлэгч байрлуулах ёстой вэ?
7. Бүхэл тооны квадратыг бүтэн квадрат тоо, бүхэл тооны кубыг бүтэн куб тоо гэж нэрлэе.
- $k$ нь бүхэл тоо байхад $3k-2$ тоог нэг бүтэн квадрат, хоёр бүтэн кубийн нийлбэрт задалж болохыг батал.
- Ямар ч бүхэл тоог нэг бүтэн квадрат, гурван бүтэн кубийн нийлбэрт задалж болохыг батал.