Заавар. 4-т хуваагдах тооны шинж ашигла.

Бодолт. Ийм $a$, $b$ тоонууд олдохгүй гэдгийг баталъя. Эсрэгээс нь олддог гэе. $a^b$ нь $222$-д хуваагддаг тул $a$ тэгш тоо байна. Нөгөө талаас $b>1$ тул $a^b$ нь $4$-д хуваагдана. Гэтэл $222$-р төгссөн тоо 4-д хуваагдахгүй тул зөрчил үүсэв.

Заавар. $1-x$, $1-y$, $1-z$ ба $1+x$, $1+y$, $1+z$ тоонууд эерэг тоонууд тул Кошийн тэнцэтгэл биш ашиглах боломжтой.

Бодолт. $t=\dfrac{x+y+z}{3}$ гэвэл $t\in]-1;1[$ ба Кошийн тэнцэтгэл бишээр $$\dfrac{1}{(1-x)(1-y)(1-z)}+\dfrac{1}{(1+x)(1+y)(1+z)}\ge\dfrac{1}{(1-t)^3}+\dfrac{1}{(1+t)^3}$$ болно. Одоо $$\dfrac{1}{(1-t)^3}+\dfrac{1}{(1+t)^3}\ge2$$ болохыг батлахад хангалттай. (Үнэндээ энэ тэнцэтгэл биш нь анхны тэнцэтгэл бишийн $x=y=z=t$ байх тухайн тохиолдол юм). $1\pm t>0$ тул $$(1+t)^3+(1-t)^3\ge2(1-t^2)^3\Leftrightarrow 2+6t^2\ge 2\ge 2(1-t^2)^3$$ илэрхий тэнцэтгэл биш болж байна. Тэнцэлдээ хүрэх нөхцөл нь $x=y=z=t=0$ байна.

Заавар. $AB$ тал болон $AC$ суурийн дундаж перпендикулярын огтлолцолын цэг $D$ нь $B$ цэгтэй давхцахыг харуул.

Бодолт. Олонлог сургуулийн багш Түвшинжаргалын ирүүлсэн бодолт. 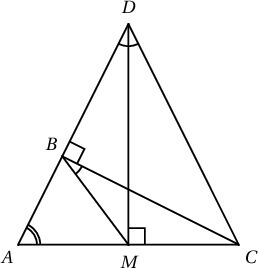$MD\perp AC$, $AB\cap MD=D$ гэе. $\measuredangle AMD=90^\circ$ тул $\measuredangle MBC=\measuredangle MDA$. $AD=DC$ тул $\measuredangle MDA=\measuredangle MDC$ байна. Иймд $MBDC$ дөрвөн өнцөгт тойрогт багтана. $\measuredangle DMC=90^\circ$ тул $\measuredangle CBD=90^\circ$ буюу $\measuredangle ABC=90^\circ$ болно. Гэтэл $\triangle ABC$ хурц өнцөгт гэж өгөгдсөн тул $B\equiv D$ байна.

Заавар. Энэ үйлдлээр 10 модулаар тэнцүү байх чанар хадгалагдана.

Бодолт. Хэрэв $a\equiv b\pmod{10}$ байсан бол эсвэл $a\pm 1\equiv b\pm 1\pmod{10}$ байна, эсвэл $a\pm1\equiv b\mp9\pmod{10}$ байна. Анх 10 модулаар тэнцүү хос нийт 5 ширхэг байгаа тул энэ чанар хадгалагдах ёстой. Самбарт сөрөг тоо бичигдэхгүй тул ялгаатай тоонуудын маань нийлбэр хамгийн багадаа $$0+1+2+3+4+10+11+12+13+14=70$$ байна. Гэтэл анх байсан тоонуудын нийлбэр $60$ ба өгөгдсөн үйлдлүүдээр нийлбэр хадгалагдах ёстой. Иймд бүх тоонуудыг ялгаатай болгох боломжгүй.