Заавар. Шурын тэнцэтгэл бишээр $$\sum(a^5+a^3bc)\ge \sum(a^4b+ab^4)$$ байна.

Бодолт. I сургуулийн 11-р ангийн сурагч Н. Бямбасүрэнгийн бодолт.

$$\dfrac{a^2}{a^2+b+c}+\dfrac{b^2}{b^2+a+c}+\dfrac{c^2}{c^2+a+b}\le\dfrac{3}{2}$$ гэж баталъя. $$\begin{align*} \text{ЗГТ}&=\dfrac{\sum a^2(b^2+a+c)(c^2+a+b)}{\prod(a^2+b+c)}\\ &=\dfrac{3a^2b^2c^2+2\sum(a^3b^2+a^2b^3)+\sum a^4+ \sum (a^3b+ab^3)+abc(a+b+c)}{a^2b^2c^2+\sum(a^3b^2+a^2b^3)+\sum a^4+\sum (a^3b+ab^3)+abc(a+b+c)+\sum(a^2b+ab^2)+2abc}\\ &\le\dfrac32 \end{align*}$$ гэж батална. Эндээс $$\begin{align*} 6a^2b^2c^2&+4\sum(a^3b^2+a^2b^3)+2\sum a^4+ 2\sum (a^3b+ab^3)+2abc(a+b+c)\\ &\le 3a^2b^2c^2+3\sum(a^3b^2+a^2b^3)+3\sum a^4+3\sum (a^3b+ab^3)+3abc(a+b+c)+3\sum(a^2b+ab^2)+6abc \end{align*}$$ буюу $$3a^2b^2c^2+\sum(a^3b^2+a^2b^3)\le \sum a^4+\sum(a^3b+ab^3)+abc(a+b+c)+3\sum(a^2b+ab^2)+6abc$$ гэж батлахад хангалттай. $$\begin{align*} (a+b+c)\cdot\text{БГТ} &=(a+b+c)(a^4+b^4+c^4)+(a+b+c)\sum(a^3b+ab^3)\\ &{~~~}+12abc(a+b+c)+\dfrac12(a+b+c)^2\sum(a^2b+ab^2)\\ &=\sum a^5+\sum(a^4b+ab^4)+\sum(a^4b+ab^4+a^3b^2+a^2b^3+a^3bc+ab^3c)\\ &{~~~}+12abc(a+b+c)+\dfrac12\sum(a^4b+a^3b^2+a^2b^3+ab^4+a^2bc^2+ab^2c^2)+{}\\ &{~~~}+\sum(a^3b^2+a^2b^3+a^3bc+a^2b^2c+a^2b^2c+ab^3c)\\ &=\sum a^5+\dfrac52\sum(a^4b+ab^4)+\dfrac52(a^3b^2+a^2b^3)+2abc(a^2+b^2+c^2)\\ &{~~~}+12abc(a+b+c)+\dfrac12\sum\big(a^2bc^2+ab^2c^2+2(a^3bc+a^2b^2c+a^2b^2c+ab^3c)\big)\\ &=2abc(a+b+c)^2+\sum (a^5+a^3bc)+\dfrac52\sum (a^4b+ab^4)+\dfrac52(a^3b^2+a^2b^3)\\ &{~~~}+abc(a^2+b^2+c^2)+\dfrac12\left\{2abc(ab+bc+ca)+2\big(2abc(ab+bc+ca)+2abc(a^2+b^2+c^2)\big)\right\}\\ &\ge 2abc(a+b+c)^2+\sum(a^3b^2+a^2b^3)+\dfrac52\sum(a^3b^2+a^2b^3)+\dfrac52\sum(a^3b^2+a^2b^3)\\ &{~~~}+abc(a^2+b^2+c^2)+abc(a^2+b^2+c^2)+abc(ab+bc+ca)+2abc(ab+bc+ca)+2abc(a^2+b^2+c^2)\\ &\ge 72abc+2abc(a+b+c)^2+6\sum(a^3b^2+a^2b^3)\\ &=72abc+72abc+6\sum(a^3b^2+a^2b^3)\\ &=\dfrac23\cdot 6^3\cdot abc+6\sum(a^3b^2+a^2b^3)\\ &=\dfrac23\cdot (a+b+c)^3\cdot abc+6\sum(a^3b^2+a^2b^3)\\ &\ge 18a^2b^2c^2+6\sum(a^3b^2+a^2b^3) \end{align*}$$ болж батлагдав. Шурын тэнцэтгэл биш ашигласан тул $a=b=c=2$ эсвэл $a=b=3$, $c=0$ (эдгээрийн сэлгэмэл) үед хамгийн их утгаа авна.

Заавар. $ACME$ параллелограмм байгуулаад $EN$ хэрчмийн дундаж цэг $F$ гээд $AF$ нь $B$ өнцгийн биссектристэй параллел болохыг харуул.

Бодолт. Т. Хулан багшийн бодолт. 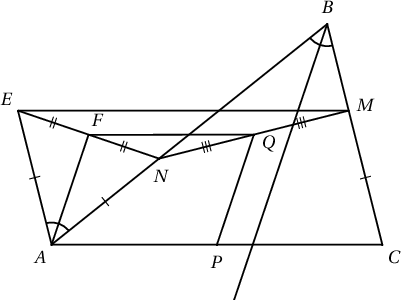Зааварт дурдсан $ACME$ параллелограмын байгуулбал $AEN$ нь адил хажуут гурвалжин болно. Түүний $AF$ биссектрис нь медиан болох тул $EF=FN$ байна. Түүнчлэн $NQ=QM$ тул $FQ$ нь $NME$ гурвалжны дундаж шугам болно. Түүнчлэн $AP$ нь $AC$-ийн хагас тул $AFQP$ параллелограм болно. Иймд $QP\parallel AF$ ба $AF$ нь $B$ өнцгийн биссектристэй параллел тул батлах зүйл батлагдав.

Заавар. $p-1=n^2$ гэж харуул.

Бодолт. Т. Базар багшийн бодолт.

$2n\mid p-1$ гэдгээс $p-1=2nk$ байна. Мөн $n < p$ байна. $p\mid n^4-1=(n-1)(n+1)(n^2+1)$ гэдгээс $p\mid n-1$, $p\mid n+1$ эсвэл $p\mid n^2+1$ байна. $p\mid n\pm 1$ үед $2nk+1=p\le n\pm +1$ болж зөрчил үүснэ. Иймд $p\mid n^2+1$ байна. $p\le n^2+1\Rightarrow 2k\le n$ болно. Хэрэв $2k < n$ бол $p\mid n^2+1-p=n^2-2nk=n(n-2k)$ ба $(p,n)=(p,n-2k)=1$ тул зөрчил үүснэ. Иймд $2k=n$ болно. Эндээс $p-1=n^2$ болов.