Бага сунгаа V, 5-р анги

Бага сунгаа V, 5-р анги   

Бодлогын тоо: 4    Хугацаа: 120 мин

1. Үлгэрийн орны 1 өдөр нь хэдэн цагаас, 1 цаг нь хэдэн минутаас, 1 минут нь хэдэн секундээс тогтоно. Хэрэв үлгэрийн орны 1 өдөр 77 минутаас, 1 цаг нь 91 секундээс тогтдог бол 1 өдөр хэдэн секундээс тогтох вэ?

Заавар Бодолт
Заавар. Цагийн минутын тоо нь $77$ ба $91$ тоонуудын ерөнхий хуваагч байна.

Бодолт. $77=1\cdot 77=7\cdot 11$ ба $91=1\cdot 91=7\cdot 13$ гэж хоёр тооны үржвэрт задарна. Цагийн минутын тоо нь аль аль үржигдэхүүнд орж байгаа тул $1$ эсвэл $7$ байна. Нөгөө талаас цаг ба минут нь өөр хэмжээ заах ёстой тул цагийн минутын тоо 1 байж болохгүй. Иймд цагийн минутын тоо нь $7$ болно. Иймд өдрийн цагийн тоо нь $11$ ба минутын секундын тоо нь $13$ тул нэг өдөрт $11\cdot 7\cdot 13=1001$ секунд байна.

2. Наадамд 2018 бөх барилдсан бол нийт хэдэн барилдаан болсон бэ? (Хэрэв аль нэг даваанд сондгой тооны бөх үлдвэл хамгийн том цолтой нь барилдахгүй өнжиж дараагийн даваанд барилдана).

Заавар Бодолт
Заавар. Барилдаан бүрд яг нэг бөх хасагдана.

Бодолт. Барилдаан бүрд яг нэг бөх хасагдах ба хамгийн сүүлд 1 бөх үлдэх тул нийт $2018-1=2017$ барилдаан болжээ.

3. Хэдэн натурал тооны аль ч тоо нь бусад тоонуудынхаа нийлбэрээс 7-оор бага бол эдгээр тоонуудыг ол.

Заавар Бодолт
Заавар. Ямар нэг тоог сонгоод бусдынх нь нийлбэр дээр нэмэхэд нэг талаас бүх тоонуудын нийлбэр, нөгөө талаас сонгосон тоог хоёр дахин аваад 7-г нэмэхтэй тэнцүү байна. Иймд өгсөн натурал тоонууд өөр хоорондоо тэнцүү байна.

Бодолт. Сонгосон тоог бусад тоонуудын нийлбэрээс хасвал 7 гарна. Заавар ёсоор бүх тоонууд тэнцүү тул энэ нь сонгосон тоог бүх тоонуудын тооноос 2-оор цөөн удаа нэмэхэд гарна. Иймд сонгосон тоо нь 7-г хуваадаг буюу 1 эсвэл 7 байх боломжтой.

Эхний тохиолдолд 9 ширхэг 1, хоёр дахь тохиолдолд 3 ширхэг 7 байна.

4. Гурвалжны нэг тал дээр 5 цэг, нөгөө тал дээр 3 цэг, гурав дахь тал дээр 2 цэг тэмдэглэв. Тэмдэглэгдсэн цэгүүд дээр оройтой хэчнээн гурвалжин зурж болох вэ?

Заавар Бодолт
Заавар. Ийм гурвалжнуудын суурь нь аль нэг тал дээр, эсвэл 3 орой нь 3 өөр тал дээр байх боломжтой.

Бодолт.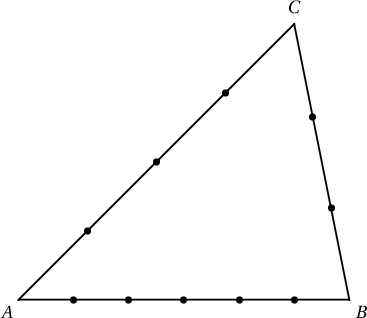
Гурван тал дээр оройтой гурвалжны тоо $5\cdot 3\cdot 2=30$, $AB$ тал дээр суурийг $C_5^2=\dfrac{5!}{(5-2)!\cdot 3!}=10$ янзаар сонгох ба оройг $3+2=5$ янзаар сонгох тул $10\cdot 5=50$ гурвалжин, $AC$ тал дээр суурийг $C_3^2=3$ янзаар сонгох ба оройг $5+2=7$ янзаар сонгох тул $3\cdot 7=21$ гурвалжин, $BC$ тал дээр суурийг нэг янзаар оройг $5+3=8$ янзаар сонгох тул $8$ гурвалжин байна. Иймд нийтдээ $$30+50+21+8=109$$ гурвалжин байна.