МУБИС-ийн олимпиад 2019, 2-р анги
Бодлогын тоо: 4 Хугацаа: 80 мин
1. Эмээ шатрын хөлгийн хээтэй дэвсгэрээр муурандаа $5\times5$ хэмжээтэй дэвсгэр хийж өгөх болов. Зураасны дагуу 3 хэсэгт хувааж эвлүүлэн оёв. Муурын дэвсгэр мөн шатрын хөлгийн хээтэй болсон бол эмээ хэрхэн хувааж эвлүүлсэн бэ?


2. Ялгаатай хоёр цифрээр бичигдэх 3 оронтой тоо хэд байдаг вэ?
Заавар Бодолт
Заавар. Бүх 3 оронтой тооны тооноос 3 ялгаатай цифрээр бичигдсэн, 3 ижил цифрээр бичигдсэн тоонуудын тоог хасахад гарна.
Бодолт. 3 оронтой тооны тоо $999-99=900$, үүнээс цифр давтагдаагүй нь $9\cdot 9\cdot 8=648$ ба 3 ижил цифрээр бичигдэх $9$ тоог хасвал
$$900-648-9=243$$
болно.
3. Зурагт дүрслэгдсэн 4 жижиг гурвалжнаас бүтсэн 3 гурвалжны тоонуудын нийлбэр тэнцүү байхаар 1-ээс 10 тоонуудыг байрлуулах тохиолдлуудыг үзүүл.
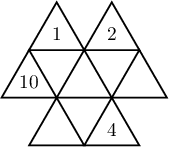

Заавар Бодолт
Заавар. Голын гурвалжинд бичигдэх тоог 4 жижиг гурвалжнаас бүтэх 3 гурвалжны тоонуудын нийлбэрийг ашиглан ол.
Бодолт. Голын нүдэнд бүчигдэх тоог $a$ гэвэл гурван гурвалжны тоонуудын нийлбэр нь
$$1+2+3+4+5+6+7+8+9+10+2a=55+2a$$
болох ба энэ нийлбэр 3-д хуваагдах ёстой. Иймд $a$ нь 3-д хуваахад 1 үлдэгдэл өгдөг тоо байна. $1,4,10$ нь аль хэдийн бичигдсэн байгаа тул голд байгаа тоо нь $7$ ба гурвалжин тус бүрд бичигдэх тоонуудын нийлбэр $\dfrac{55+7\cdot 2}{3}=23$ байна. Иймд
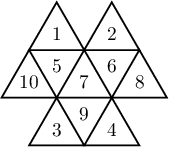 байгуулалт хийж болно. Түүнчлэн 6 ба 8, 3 ба 9 тоонуудын байрыг сольж өөр байгуулалт гарган авах боломжтой.
байгуулалт хийж болно. Түүнчлэн 6 ба 8, 3 ба 9 тоонуудын байрыг сольж өөр байгуулалт гарган авах боломжтой.

4. Хүү, охин хоёр нэгээс эхлэн хэсэг тоог дэс дарааллаар нь бичив. Хүү бүх сондгой тоог нэмж, харин охин бүх тэгш тоог нэмжээ. Гарсан тоонуудын зөрөө 10 гарсан бол бүх тооны нийлбэр хэд байж болох вэ?
Заавар Бодолт
Заавар. Хүүгийн нийлбэр охины нийлбэрээс 10-аар их байх, охины нийлбэр хүүгийн нийлбэрээс 10-аар их байж болох 2 тохиолдол байгааг анхаар.
Бодолт. Хэрвээ тэгш ширхэг тоо бичсэн бол охины нийлбэр, сондгой ширхэг тоо бичсэн бол хүүгийн нийлбэр их байна. Тэгш ширхэг тоо бичсэн бол охин ба хүүгийн нийлбэрийн зөрөө $10$ болохын тулд
$$(2-1)+(4-3)+(6-5)+\cdots+(18-17)+(20-19)=10$$
сондгой ширхэг тоо бичсэн бол хүү ба охины нийлбэрийн зөрөө $10$ болохын тулд
$$1+(3-2)+(5-4)+(7-6)+\cdots+(19-18)=10$$
байна. Иймд бүх тооны нийлбэр
$$1+2+3+\cdots+20=210$$
эсвэл
$$1+2+3+\cdots+19=191$$
байх боломжтой.

