МУБИС-ийн олимпиад 2019, 8-р анги
Бодлогын тоо: 4 Хугацаа: 150 мин
1. $1+5\cdot 2^m=n^2$ тэгшитгэлийн эерэг бүхэл тоон бүх шийдийн хосуудыг ол.
2. $a$, $b$, $c$, $d$ нь $ab+cd=1$ байх эерэг бодит тоонууд бол
$$(a+d)^2+(c+b)^2\le \dfrac{a}{b}+\dfrac{b}{a}+\dfrac{c}{d}+\dfrac{d}{c}$$
тэнцэтгэл бишийг батал. Тэнцэлдээ хүрэх нөхцөлийг тогтоо.
Заавар Бодолт
Заавар. \begin{align*}
\dfrac{a}{b}&+\dfrac{b}{a}+\dfrac{c}{d}+\dfrac{d}{c}=\dfrac{1}{abcd}(a^2cd+b^2cd+c^2ab+d^2ab)\\
&=\dfrac{1}{abcd}\big(ac(ad+bc)+bd(bc+ad)\big)=\dfrac{1}{abcd}(ad+bc)(ac+bd)
\end{align*}
Бодолт. Я. Лхагвагэрэл багшийн ирүүлсэн бодолт.
Зааварт гарсан илэрхийлэл ба $ab+cd=1$ болохыг ашиглавал $$abcd\big((a+d)^2+(b+c)^2\big)\le (ad+bc)(ac+bd)$$ буюу $$abcd\big(a^2+b^2+c^2+d^2+2ad+2bc)\le (ab+cd)(ad+bc)(ac+bd)$$ гэж батлахад хангалттай. Хаалт задалж эмхэтгэвэл \begin{align*} a^3bcd+ab^3cd&+abc^3d+abcd^3+2a^2d^2bc+2b^2c^2ad\\ &\le (ab+cd)(a^2cd+b^2cd+c^2ab+d^2ab)\\ &=a^3bcd+ab^3cd+a^2b^2c^2+a^2b^2d^2+a^2c^2d^2+b^2c^2d^2+c^3abd+d^3abc \end{align*} буюу $$2a^2d^2bc+2b^2c^2ad\le a^2b^2c^2+a^2b^2d^2+a^2c^2d^2+b^2c^2d^2$$ гэж батлах хэрэгтэй. Кошийн тэнцэтгэл бишээр $$2b^2c^2ad=2\sqrt{b^4c^4a^2d^2}\le a^2b^2c^2+b^2c^2d^2$$ $$2a^2d^2bc=2\sqrt{a^4d^4b^2c^2}\le a^2b^2d^2+a^2c^2d^2$$ тэнцэтгэл бишүүдийг нэмэхэд батлах зүйл батлагдаж байна. Тэнцэлдээ хүрэх нөхцөл нь сүүлийн тэнцэтгэл бишээс $a=d$, $b=c$ байна. Эндээс $ab+cd=1$ тул $ab=\dfrac12$ болно.
Зааварт гарсан илэрхийлэл ба $ab+cd=1$ болохыг ашиглавал $$abcd\big((a+d)^2+(b+c)^2\big)\le (ad+bc)(ac+bd)$$ буюу $$abcd\big(a^2+b^2+c^2+d^2+2ad+2bc)\le (ab+cd)(ad+bc)(ac+bd)$$ гэж батлахад хангалттай. Хаалт задалж эмхэтгэвэл \begin{align*} a^3bcd+ab^3cd&+abc^3d+abcd^3+2a^2d^2bc+2b^2c^2ad\\ &\le (ab+cd)(a^2cd+b^2cd+c^2ab+d^2ab)\\ &=a^3bcd+ab^3cd+a^2b^2c^2+a^2b^2d^2+a^2c^2d^2+b^2c^2d^2+c^3abd+d^3abc \end{align*} буюу $$2a^2d^2bc+2b^2c^2ad\le a^2b^2c^2+a^2b^2d^2+a^2c^2d^2+b^2c^2d^2$$ гэж батлах хэрэгтэй. Кошийн тэнцэтгэл бишээр $$2b^2c^2ad=2\sqrt{b^4c^4a^2d^2}\le a^2b^2c^2+b^2c^2d^2$$ $$2a^2d^2bc=2\sqrt{a^4d^4b^2c^2}\le a^2b^2d^2+a^2c^2d^2$$ тэнцэтгэл бишүүдийг нэмэхэд батлах зүйл батлагдаж байна. Тэнцэлдээ хүрэх нөхцөл нь сүүлийн тэнцэтгэл бишээс $a=d$, $b=c$ байна. Эндээс $ab+cd=1$ тул $ab=\dfrac12$ болно.
Заавар Бодолт
Заавар. Баруун гар талыг $ab+cd=1$ тоогоор үржүүлээд гарсан тэнцэтгэл бишийг батал.
Бодолт. $$\text{ЗГТ}=a^2+2ad+d^2+c^2+2cb+b^2$$
ба
\begin{align*}
\text{БГТ}&=\dfrac{a}{b}+\dfrac{b}{a}+\dfrac{c}{d}+\dfrac{d}{c}\\
&=(ab+cd)\left(\dfrac{a}{b}+\dfrac{b}{a}+\dfrac{c}{d}+\dfrac{d}{c}\right)\\
&=a^2+b^2+\dfrac{abc}{d}+\dfrac{abd}{c}+\dfrac{acd}{b}+\dfrac{bcd}{a}+c^2+d^2
\end{align*}
тул
$$2ad+2bc\le \dfrac{abc}{d}+\dfrac{abd}{c}+\dfrac{acd}{b}+\dfrac{bcd}{a}$$
гэж батлахад хангалттай.
Энэ нь
$$2ad=2\sqrt{\dfrac{acd}{b}\cdot\dfrac{abd}{c}}\le\dfrac{acd}{b}+\dfrac{abd}{c}$$
$$2bc=2\sqrt{\dfrac{abc}{d}\cdot\dfrac{bcd}{a}}\le\dfrac{abc}{d}+\dfrac{bcd}{a}$$
тэнцэтгэл бишүүдийн нийлбэр юм. Тэнцэлдээ хүрэх нөхцөл нь $b=c$, $a=d$ ба $ab=\dfrac12$ байна.
3. Зөвхөн 1, 5, 9 цифрүүдээс тогтсон 12 оронтой, 37-д хуваагддаг тооны цифрүүдийн нийлбэр 76-тай тэнцүү байж болох уу?
4. $\measuredangle ADC=30^\circ$ байх $ABCD$ гүдгэр дөрвөн өнцөгтийн хувьд $BD=AB+BC+AC$ бол $BD$ диагонал нь $\measuredangle ABC$-ийн биссектрисс болохыг харуул.
Заавар Бодолт
Заавар. $B$ цэгийг $CD$, $AD$ шулуунуудын хувьд тэгш хэмээр хувиргаж үүсэх цэгүүдийг сонирхоорой.
Бодолт. Я. Лхагвагэрэл багшийн бодолт.
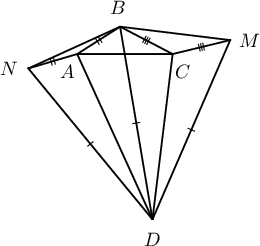$B$ цэгийг $CD$, $AD$ шулуунуудын хувьд тэгш хэмээр хувиргаж үүсэх цэгүүдийг харгалзан $M$, $N$ гэе. Эндээс $ND=BD=MD$ гэж гарна. $\measuredangle BDA=\beta$, $\measuredangle BDC=\alpha$ гэвэл
$$\triangle NDM\colon\measuredangle NDM=2(\alpha+\beta)=2\cdot 30^\circ=60^\circ$$
болно. Иймд $\triangle NDM$ зөв гурвалжин болно. Нөгөө талаас
$$MN=ND=BD=BA+AC+CB=NA+AC+CM$$
байна. Гурвалжны тэнцэтгэл бишээр
$$NA+AC+CM\ge MN$$
тул $A$ ба $C$ цэгүүд $MN$ дээр оршино. Эндээс
$$\measuredangle ABD=\measuredangle AND=60^\circ$$
$$\measuredangle CBD=\measuredangle CMD=60^\circ$$
буюу $\measuredangle ABD=60^\circ=\measuredangle CBD$ болж бодлого бодогдов.