МУБИС-ийн олимпиад 2019, 7-р анги
Бодлогын тоо: 4 Хугацаа: 150 мин
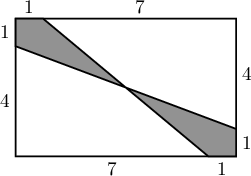
1. Будагдсан хэсгийн талбайг ол.
Заавар Бодолт
Заавар.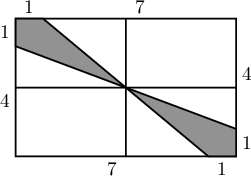 
Нийт дүрсийн талбайгаас цагаан дүрсийн талбайн нийлбэрийг хасаж бод.
Бодолт. Зааварт өгсөн цагаан гурвалжнуудыг хоёр, хоёроор нь тэгш өнцөгт үүсгэж талбайг нь олбол
$$1.5\cdot4+3\cdot 2.5=13.5$$
ба хоёр цагаан тэгш өнцөгтийн талбайн нийлбэр
$$2\cdot 2.5\cdot4=20$$
тул будагдаагүй хэсгийн талбай $13.5+20=33.5$ болно. Том тэгш өнцөгтийн талбай $5\cdot 8=40$ тул будагдсан хэсгийн талбай
$$40-33.5=6.5$$
байна.
2. $S(n)$-ээр $n$ натурал тооны цифрүүдийн нийлбэрийг тэмдэглэе. Тэгвэл $S(n)=2019\cdot S(3n)$ байх $n$ тоо олдох уу?
Заавар Бодолт
Заавар. $n=333\ldots 3444$ хэлбэрийн тоо сонирх.
Бодолт. Б. Мөнхтулгын ирүүлсэн бодолт.
$n=\underbrace{333\ldots 3}_k444$ гэвэл $3n=1\underbrace{00\ldots 0}_{k}332$ ба $S(n)=3k+12$, $S(3n)=9$ байна. $$S(n)=2018\cdot S(3n)\Rightarrow 3k+12=2019\cdot 9$$ буюу $k=6053$ байна. Иймд $n=\underbrace{333\ldots 3}_{6053}444$ тооны хувьд бодлогын нөхцөл биелэнэ.
$n=\underbrace{333\ldots 3}_k444$ гэвэл $3n=1\underbrace{00\ldots 0}_{k}332$ ба $S(n)=3k+12$, $S(3n)=9$ байна. $$S(n)=2018\cdot S(3n)\Rightarrow 3k+12=2019\cdot 9$$ буюу $k=6053$ байна. Иймд $n=\underbrace{333\ldots 3}_{6053}444$ тооны хувьд бодлогын нөхцөл биелэнэ.
3. $\{1,2,3,4,\dots,2019\}$ олонлогийг хос хосоороо үл огтлолцох, аль ч олонлог нь дараалсан 2 тоо агуулдаггүй байхаар гурван дэд олонлогт хэдэн янзаар хувааж болох вэ?
4. Зөв зургаан өнцөгтийг $n$ ширхэг тэнцүү олон өнцөгтөд хувааж чаддаг бол $n$ тоог гоё тоо гэе. Жишээ нь $n=6$ бол гоё тоо болохыг зурагт үзүүлэв. $n$ болон $2^n+n$ тоонууд хоёулаа гоё тоо байх $n$ төгсгөлгүй олон олдохыг харуул.
