МУБИС-ийн олимпиад 2019, 9-р анги
Бодлогын тоо: 4 Хугацаа: 180 мин
1. $\sqrt{\underbrace{11\ldots1}_{2017}\underbrace{22\ldots2}_{2018}5}$ тооны бүхэл хэсгийн цифрүүдийн нийлбэрийг ол.
Заавар Бодолт
Заавар. $\underbrace{11\ldots1}_{n-1}\underbrace{22\ldots2}_{n}5$ тоо ямар тооны квадрат болох вэ?
$n=1$ үед $25=5^2$, $n=2$ үед $1225=35^2$, $n=3$ үед $112225=335^2$ болохыг шалгахад төвөггүй. Эндээс $$\underbrace{11\ldots1}_{2017}\underbrace{22\ldots2}_{2018}5=\underbrace{33\ldots3}_{2017}5^2$$ гэсэн таамаглал дэвшүүлж болохоор байна.
$n=1$ үед $25=5^2$, $n=2$ үед $1225=35^2$, $n=3$ үед $112225=335^2$ болохыг шалгахад төвөггүй. Эндээс $$\underbrace{11\ldots1}_{2017}\underbrace{22\ldots2}_{2018}5=\underbrace{33\ldots3}_{2017}5^2$$ гэсэн таамаглал дэвшүүлж болохоор байна.
Бодолт. $$\underbrace{11\ldots1}_{n-1}\underbrace{22\ldots2}_{n}5=\underbrace{33\ldots3}_{n-1}5^2$$
гэж баталъя. Нэг талаас
\begin{align*}
\underbrace{11\ldots1}_{n-1}\underbrace{22\ldots2}_{n}5&=\dfrac{10^{n-1}-1}{9}\cdot 10^{n+1}+2\cdot\dfrac{10^{n}-1}{9}\cdot 10+5\\
&=\dfrac{10^{2n}-10^{n+1}}{9}+\dfrac{2\cdot 10^{n+1}-20}{9}+\dfrac{45}{9}\\
&=\dfrac19(10^{2n}+10^{n+1}+25)
\end{align*}
Нөгөө талаас
\begin{align*}
\underbrace{33\ldots3}_{n-1}5^2&=(\underbrace{33\ldots3}_{n-1}\cdot 10+5)^2\\
&=(\underbrace{33\ldots3}_{n-1}\cdot 10)^2+2\cdot\underbrace{33\ldots3}_{n-1}\cdot 10\cdot 5+25\\
&=\left(\dfrac{10^{n-1}-1}{3}\cdot 10\right)^2+\dfrac{10^{n-1}-1}{3}\cdot 10^2+25\\
&=\left(\dfrac{10^{n-1}-1}{3}\cdot 10\right)^2+\dfrac{10^{n-1}-1}{3}\cdot 10^2+25\\
&=\dfrac{(10^n-10)^2}{9}+\dfrac{3\cdot 10^{n+1}-300}{9}+\dfrac{225}{9}\\
&=\dfrac19(10^{2n}-2\cdot 10^{n+1}+100+3\cdot 10^{n+1}-300+225)\\
&=\dfrac19(10^{2n}+10^{n+1}+25)
\end{align*}
тул
$$\sqrt{\underbrace{11\ldots1}_{2017}\underbrace{22\ldots2}_{2018}5}=\underbrace{33\ldots3}_{2017}5$$
тул цифрүүдийн нийлбэр нь
$$3\cdot 2017+5=6056$$
байна.
2. $x$, $y$, $z$ нь $\dfrac{x}{y+z}+\dfrac{y}{z+x}+\dfrac{z}{x+y}=1$ нөхцөлийг хангадаг бол $\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}$ илэрхийллийн авч болох утгуудыг ол.
Заавар Бодолт
Заавар. $\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}=0$ болохыг батал.
Бодолт. \begin{align*}
\text{Илэрх.}&=\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\\
&=\dfrac{x^2}{y+z}+x+\dfrac{y^2}{z+x}+y+\dfrac{z^2}{x+y}+z-(x+y+z)\\
&=\dfrac{x(x+y+z)}{y+z}+\dfrac{y(x+y+z)}{z+x}+\dfrac{z(x+y+z)}{x+y}-(x+y+z)\\
&=(x+y+z)\left(\dfrac{x}{y+z}+\dfrac{y}{z+x}+\dfrac{z}{x+y}-1\right)\\
&=(x+y+z)\cdot 0=0
\end{align*}
3. $1,2,3,\dots,2018,2019$ тоонууд дундаас аль ч хоёр тооных нь зөрөө $4$, $5$ эсвэл $9$-тэй тэнцүү биш байх ялгаатай $624$ тоог сонгож авав. Сонгогдсон тоонуудын нэг нь $1016$ гэдгийг батал.
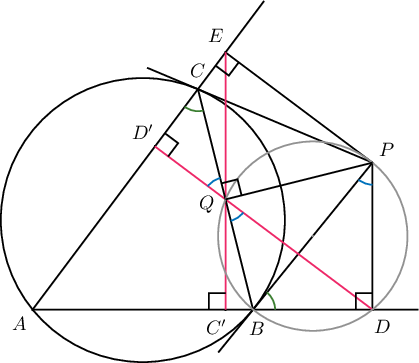
4. $ABC$ хурц өнцөгт гурвалжин $\omega$ тойрогт багтана. $\omega$ тойргийн $B$, $C$ цэгүүдэд татсан шүргэгчүүд $P$ цэгт огтлолцоно. $P$ цэгээс $AB$ ба $AC$ талуудад татсан перпендикулярын сууриуд харгалзан $D$, $E$ бол $BC$ талын дундаж цэг нь $ADE$ гурвалжны өндрүүдийн огтлолцолын цэг (орто төв) болно гэж батал.
Заавар Бодолт
Заавар. $D$ цэг ба $BC$ талын дундаж цэгийг дайруулж татсан шулуун $AC$-д перпендикуляр гэж батал.
Бодолт. $Q$ нь $BC$ талын дундаж цэг ба $DQ\cap AC=D'$, $EQ\cap AB=C'$ гэе. $P$ цэгээс татсан шүргэгчүүд тул $PB=PC$ байна. Иймд $\triangle BPC$ нь адил хажуут гурвалжин тул $BC$ талын дундаж $Q$ нь $BPC$ гурвалжны $P$ оройгоос татсан өндрийн суурь болно. $\angle PQB=\angle PDB=90^\circ$ тул $BQPD$ дөрвөн өнцөгт тойрогт багтана. Иймд
$$\angle BPD=\angle BQD=\angle CQD'$$
байна. Нөгөө талаас $AB$ нумд тулсан $\angle ACB$ нь $B$ цэгт татсан шүргэгчээр үүсэх $\angle PBD$ өнцөгтэй тэнцүү тул $\triangle PBD\sim\triangle CD'Q$ болно. Иймд $\angle QD'E=\angle BDE=90^\circ$ болов. Иймд $DD'$ нь $AED$ гурвалжны өндөр болов. Яг адилаар $EC'$ нь өндөр болох ба эдгээр дээр $Q$ цэг орших тул $Q$ цэг $AED$ гурвалжны орто центр болж батлах зүйл батлагдав.