МУБИС-ийн олимпиад 2019, 1-р анги
Бодлогын тоо: 4 Хугацаа: 45 мин
1. 
Хэсгүүдээр дараах дүрсийг эвлүүл.
2. 1-ээс 9 тоонуудыг заасан нөхцөл биелэхээр байрлуул.
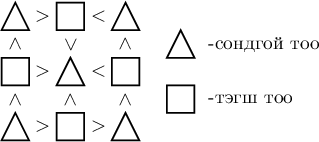
Заавар Бодолт
Заавар. Энэ төрлийн бодлогод аль болох олон шийд олбол сайн.
Бодолт.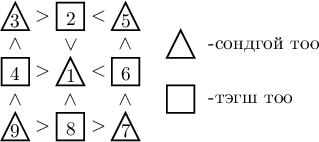 
Өөр боломжуудыг шалгаарай.
3. $\text{М}-\text{У}-\text{Б}-\text{И}=\text{C}$ тэнцэтгэлийн ижил үсэг ижил, ялгаатай үсэг ялгаатай цифрийг төлөөлнө. $\text{У}<\text{Б}<\text{И}<\text{C}$ байх бүх хариуг бичээрэй.
Заавар Бодолт
Заавар. $0<\text{У}$ бол $\text{M}=\text{У}+\text{Б}+\text{И}+\text{С}\ge1+2+3+4=10$ болно.
Бодолт. Заавар ёсоор $\text{У}=0$ байх ёстой. Иймд $\text{М}=\text{Б}+\text{И}+\text{С}\ge 1+2+3=6$ байна.
$\text{М}=6$ бол зөвхөн $\text{Б}=1$, $\text{И}=2$, $\text{С}=3$ гэсэн шийд байна.
$\text{М}=7$ бол зөвхөн $\text{Б}=1$, $\text{И}=2$, $\text{С}=4$ гэсэн шийд байна.
$\text{М}=8$ бол $\text{Б}=1$, $\text{И}=2$, $\text{С}=5$; $\text{Б}=1$, $\text{И}=3$, $\text{С}=4$ гэсэн хоёр шийд байна.
$\text{М}=9$ бол $\text{Б}=1$, $\text{И}=2$, $\text{С}=6$; $\text{Б}=1$, $\text{И}=3$, $\text{С}=5$; $\text{Б}=2$, $\text{И}=3$, $\text{С}=4$ гэсэн гурван шийд байна.
Иймд нийт $1+1+2+3=7$ шийдтэй.
$\text{М}=6$ бол зөвхөн $\text{Б}=1$, $\text{И}=2$, $\text{С}=3$ гэсэн шийд байна.
$\text{М}=7$ бол зөвхөн $\text{Б}=1$, $\text{И}=2$, $\text{С}=4$ гэсэн шийд байна.
$\text{М}=8$ бол $\text{Б}=1$, $\text{И}=2$, $\text{С}=5$; $\text{Б}=1$, $\text{И}=3$, $\text{С}=4$ гэсэн хоёр шийд байна.
$\text{М}=9$ бол $\text{Б}=1$, $\text{И}=2$, $\text{С}=6$; $\text{Б}=1$, $\text{И}=3$, $\text{С}=5$; $\text{Б}=2$, $\text{И}=3$, $\text{С}=4$ гэсэн гурван шийд байна.
Иймд нийт $1+1+2+3=7$ шийдтэй.
4. Бат цаасан дээр $\fbox{2}$, $\fbox{3}$, $\fbox{4}$, $\fbox{?}$ дөрвөн ялгаатай тоо бичжээ.
Тэр цаасаараа $2\times 2$ хэмжээтэй квадрат бүтээв. Хоёр дахь мөрний нийлбэр 6, хоёр дахь баганын нийлбэр 10 бол дөрөв дэх тоо хэд байж болох вэ?
Заавар Бодолт
Заавар. 2-р мөр, 2-р баганын нийлбэр тэгш тоонууд тул 2-р мөр ба 3-р баганад байгаа тоонуудын тэгш сондгой нь ижил байна.
Бодолт. Хүснэгтэд 3 сондгой тоо бичигдэх боломжгүй тул 2-р мөр, 2-р баганын тоонууд нь бүгд тэгш байх ёстой. $\fbox{2}$, $\fbox{4}$ картууд өөр мөр, баганад байгаа тохиолдолд хоёр нийлбэрийн зөрөө нь $4-2=2$ байх ёстой. Гэтэл зөрөө нь $10-6=4$ тул $\fbox{2}$, $\fbox{4}$ тоонууд 2-р мөрөнд бичигдэх ёстой. Иймд дараах боломжууд байна.
