Орчлон 2019, 8-р анги
Бодлогын тоо: 4 Хугацаа: 180 мин
1. Дэс дараалсан 3 сондгой тооны үржвэрийг олоход $\overline{ababab}$ тооноос 5 дахин бага тоо гарчээ. Ямар тоонуудыг үржүүлсэн бэ?
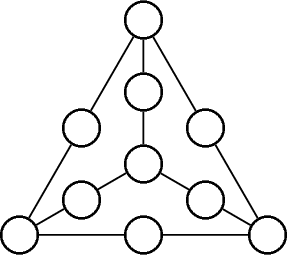
2. 6 хэрчим дээр 10 дугуйг байрлуулсан байв (зураг). Хэрчим бүр дээр байрласан 3 дугуйн голын дугуйд бичигдсэн тоо нь 2 захын дугуйд бичигдсэн 2 тооны дундажтай тэнцүү байхаар дугуйнуудад дэс дараалсан 10 ширхэг натурал тоог бичиж болох уу?

Заавар Бодолт
Заавар. Хамгийн их ба хамгийн бага тоонууд нь аль нэг хэрчмийн дундаж дээр байрлах боломжгүй.
Бодолт. Хамгийн бага нь $n$ бол хамгийн их нь $n+9$ байна. Эдгээр тоонууд нь аль нэг хэрчмийн дундаж дээр байрлах боломжгүй юм. Нөгөө талаас эдгээр тоонуудын нийлбэр $2n+9$ нь сондгой тоо тул дундаж нь бүхэл тоо байх боломжгүй тул бодлогын нөхцөл хангахаар дараалсан 10 тоо бичих боломжгүй юм.
3. Батад тус бүр 1 см, 2 см, 3 см, 4 см, 5 см, 6 см, 7 см, 8 см урттай хангалттай олон савх байжээ. Тэр савхнуудаа давхарлахгүй байрлуулж зурагт үзүүлсэн $8\,\text{см}\times 8\,\text{см}$ хэмжээтэй торыг хийхийг хүсэж байв (савхыг хугалж, нугалж болохгүй). Тэр хамгийн цөөндөө хэдэн ширхэн 1 см урттай савх ашиглах ёстой вэ?


Заавар Бодолт
Заавар. Хүрээг оролцуулалгүй бусад хэрчмүүдийн тоог хамгийн цөөндөө хэд байж болохыг ол.
Бодолт. Хүрээг оруулалгүй нийт хэдэн савх байхыг тооцъё. Эхлээд хүрээн дээр төгсгөлтэй савх нийт $4\times 7=28$ ширхэг байх ба дотоод орой бүр хамгийн цөөндөө 2 савхны төгсгөл болох ёстой тул дор хаяж $28+2\cdot 49=126$ төгсгөл байх буюу савхны тоо $126:2=63$-аас цөөнгүй байна. Түүнчлэн $e_i$-ээр $i$ урттай савхны тоог тэмдэглэвэл
$$e_1+e_2+\dots+e_8\ge 63$$
тул дотоод хэсгийн нийт урт
$$14\cdot 8=1\cdot e_1+2\cdot e_2+\dots+8\cdot e_8\ge e_1+2(e_2+\dots+e_8)\ge e_1+2(63-e_1)$$
байна. Иймд $14\le e_1$ болно. $e_1=14$ байхаар торыг хийж болохыг харуулъя.


4. $2\times2019$ хэмжээтэй хүснэгт өгөгджээ. 2 тоглогч ээлжлэн хүснэгтийн аль нэг нүдийг 1-р тоглогч хөх өнгөөр, 2-р тоглогч улаан өнгөөр будна (будсан нүдийг дахиж будахгүй). Хүснэгтийн бүх нүд будагдаж дуусахад, хүснэгтийн ижил өнгөтэй хөрш 2 нүдний тоо $a$ ба ялгаатай өнгөтэй хөрш 2 нүдний тоо $b$-г олно. $a > b$ байвал тоглоомонд 1-р тоглогч, харин $a < b$ байвал $2$-р тоглогч хожино (ерөнхий талтай нүднүүдийг хөрш гэж тооцно). Зөв тоглолтод аль тоглогч хожих вэ?