ММО-55, II даваа, 7-р анги
Бодлогын тоо: 4 Хугацаа: 180 мин
1. Аль ч мөр, аль ч багана ба хоёр диагоналийн дагуух тоонуудын нийлбэр ижил байхаар нүд бүрт нь натурал тоо бичигдсэн $3\times 3$ хэмжээтэй квадратыг шидэт квадрат гэдэг. Шидэт квадратын хоёр тоо зурагт дүрсэлсэн байдлаар өгөгджээ. Хаа нэгтээ 9 бичигдэхээр шидэт квадратыг гүйцээж бөглө (бүх боломжит байдлаар).
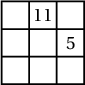

Заавар Бодолт
Заавар. 9 цифр байрлах нүд тус бүр дээр бод.
Бодолт. 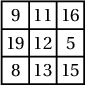
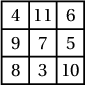
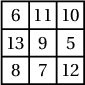
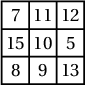
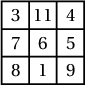 байна.
байна.
Одоо үлдсэн 2 нүдэнд 9 байрлах үед шидэт квадрат байхаар бөглөж чадахгүй гэж баталъя. Зүүн доод буланд 9 байх үед баталъя. Нөгөө тохиолдолд яг адил аргаар батлагдана. Голын нүдэнд $a$ тоо байсан гэе. Мөр, багана ба диагоналын элементүүдийн нийлбэр тэнцүү $S$ байг. Тэгээд мөр баганы нийлбэрээс хоосон нүднүүдийг олвол болох ба диагоналын элементийн нийлбэрийг бодоход
$$9+a+S-a-7=S-16=S$$
болж зөрчил гарна.
болох ба диагоналын элементийн нийлбэрийг бодоход
$$9+a+S-a-7=S-16=S$$
болж зөрчил гарна.




 байна.
байна.Одоо үлдсэн 2 нүдэнд 9 байрлах үед шидэт квадрат байхаар бөглөж чадахгүй гэж баталъя. Зүүн доод буланд 9 байх үед баталъя. Нөгөө тохиолдолд яг адил аргаар батлагдана. Голын нүдэнд $a$ тоо байсан гэе. Мөр, багана ба диагоналын элементүүдийн нийлбэр тэнцүү $S$ байг. Тэгээд мөр баганы нийлбэрээс хоосон нүднүүдийг олвол

2. Натурал $n$ тооны цифрүүдийн нийлбэрийг $s(n)$ гэж тэмдэглэе. $s(n^2)+2s(n-1)=2019$ байх $n$ тоо олдох уу?
Заавар Бодолт
Заавар. $s(n)\equiv n\pmod{9}$ болохыг ашигла.
Бодолт. $s(n^2)+2s(n-1)=2019$ тул
$$s(n^2)+2s(n-1)\equiv n^2+2s(n-1)\equiv 2019\equiv 3\pmod{9}$$
буюу
$$(n+1)^2\equiv 6\pmod{9}$$
байна. Гэвч бүхэл тооны квадратыг 9-д хуваахад $0,1,4,7$ үлдэгдэл л өгөх боломжтой тул бодлогын нөхцөлийг хангах натурал $n$ тоо олдохгүй.
3. $a+b+c=d$ байх ямар ч $a$, $b$, $c$, $d$ дөрвөл (заавал ялгаатай байх албагүй) бүгд ижил өнгөөр будагдаагүй байхаар $1, 2, 3, 4,\ldots$ тоонуудыг улаан эсвэл хөх өнгөөр будаж болох уу?
Заавар Бодолт
Заавар. Болохгүй гэдгийг харуул. Тоонууд тэнцүү байж болохыг санаарай.
Бодолт. Тийм будалт байхгүй гэж харуулъя. Эсрэгээс нь тийм будалт олддог гэе. Энэ будалтанд 1 улаанаар будагдсан гэж үзье. Тэгээд цаашид $n$ тоо улаанаар будагдсан бол $n^R$, хөх бол $n^B$ гэнэ. $a+b+c=d$ ижил өнгөөр будагдаагүй гэдгээс $1^R+1^R+1^R=3\Rightarrow 3^B$, $3^B+3^B+3^B=9\Rightarrow 9^R$, $1^R+4+4=9^R\Rightarrow 4^B$. Эндээс
$$1^R+1^R+9^R=11\Rightarrow 11^B, 3^B+4^B+4^B=11\Rightarrow 11^R$$
болж зөрчил үүсч байна. Иймд ийм будалт олдохгүй.
4. $2\times 4$ хэмжээтэй шоколадны цуглуулгын нүд бүрд өөр өөр амттай шоколад байв. Бат хоёроос олонгүй хөрш нүдэндээ (ерөнхий талтай) шоколадтай аль нэг нүднээс шоколад авч иддэг. Бат хэдэн янзаар шоколадны цуглуулгаа идэж дуусгаж чадах вэ?
Заавар Бодолт
Заавар. Рекуррент томьёо үүсгэж тоол.
Бодолт. Дүрсээрээ тухайн дүрсийг хэчнээн янзаар идэж болох тоог тэмдэглэе. Тэгвэл
 цааш нь
цааш нь
 гэж задлаад үүсэх дүрсүүдийг төстэйгээр задалж бодъё.
гэж задлаад үүсэх дүрсүүдийг төстэйгээр задалж бодъё.



 Нүд бүр нь хоёроос олонгүй хөрш нүдтэй $k$ нүдтэй дүрсийг $k!$ янзаар идэж болох тул
Нүд бүр нь хоёроос олонгүй хөрш нүдтэй $k$ нүдтэй дүрсийг $k!$ янзаар идэж болох тул
 болно. Эндээс өмнөтэй ижил аргаар бодвол
$$4\times(5\times5!+3\times(3\times 4!+3\times 3!)+9\times(3\times 4!+3\times 3!))=6720$$
болно.
болно. Эндээс өмнөтэй ижил аргаар бодвол
$$4\times(5\times5!+3\times(3\times 4!+3\times 3!)+9\times(3\times 4!+3\times 3!))=6720$$
болно.






