ММО-55, II даваа, Бага ангийн багш
Бодлогын тоо: 6 Хугацаа: 540 мин
1. $\overline{ABCABCBBB}$ тоо нь $1$-ээс $17$ хүртэлх бүх тоонд хуваагддаг байх бүх ялгаатай $A$, $B$, $C$ цифрүүдийг ол.
Заавар Бодолт
Заавар.
Бодолт. $n = \overline{ABCABCBBB}$ гэе. $n$ тоо $5$-д хуваагдах тул $B = 5$ эсвэл $0$ байна. Мөн
$n$ тэгш тоо тул $B = 0$ болно. $n$ тоо $9$-д хуваагдах тул $2(A + C)$ тоо $9$-д хуваагдана.
Эндээс $A + C$ нь 9-д хуваагдана. $n$ тоо 16-д хуваагдах тул $C000$ тоо $16$-д хуваагдах
ёстой. Эндээс $C$ тэгш байх ёстой. Иймд $A = 7$, $C = 2$ эсвэл $A = 5$, $C = 4$ эсвэл
$A = 3$, $C = 6$ эсвэл $A = 1$, $C = 8$ байх боломжуудтай. Эндээс 108108000, 306306000,
504504000, 702702000 гэсэн тоонуудаас 17-д хуваагдах нь 306306000 тоо л юм.
2. Аль ч мөр, аль ч багана ба хоёр диагоналийн дагуух тоонуудын нийлбэр ижил байхаар нүд бүрт нь натурал тоо бичигдсэн $3\times 3$ хэмжээтэй квадратыг шидэт квадрат гэдэг. Шидэт квадратын хоёр тоо зурагт дүрсэлсэн байдлаар өгөгджээ. Хаа нэгтээ 9 бичигдэхээр шидэт квадратыг гүйцээж бөглө (бүх боломжит байдлаар).
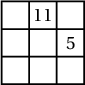

Заавар Бодолт
Заавар. 9 цифр байрлах нүд тус бүр дээр бод.
Бодолт. 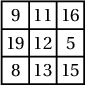
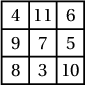
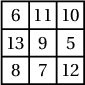
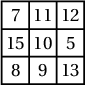
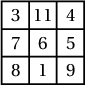 байна.
байна.
Одоо үлдсэн 2 нүдэнд 9 байрлах үед шидэт квадрат байхаар бөглөж чадахгүй гэж баталъя. Зүүн доод буланд 9 байх үед баталъя. Нөгөө тохиолдолд яг адил аргаар батлагдана. Голын нүдэнд $a$ тоо байсан гэе. Мөр, багана ба диагоналын элементүүдийн нийлбэр тэнцүү $S$ байг. Тэгээд мөр баганы нийлбэрээс хоосон нүднүүдийг олвол болох ба диагоналын элементийн нийлбэрийг бодоход
$$9+a+S-a-7=S-16=S$$
болж зөрчил гарна.
болох ба диагоналын элементийн нийлбэрийг бодоход
$$9+a+S-a-7=S-16=S$$
болж зөрчил гарна.




 байна.
байна.Одоо үлдсэн 2 нүдэнд 9 байрлах үед шидэт квадрат байхаар бөглөж чадахгүй гэж баталъя. Зүүн доод буланд 9 байх үед баталъя. Нөгөө тохиолдолд яг адил аргаар батлагдана. Голын нүдэнд $a$ тоо байсан гэе. Мөр, багана ба диагоналын элементүүдийн нийлбэр тэнцүү $S$ байг. Тэгээд мөр баганы нийлбэрээс хоосон нүднүүдийг олвол

3. $n\times n$ хэмжээтэй хүснэгтийн зүүн дээд булангаас баруун доод булан
хүртэлх диагональ дээр орших нүд бүрийн хувьд уг нүдийг агуулах мөр баганад ижил
тоо байдаггүй байхаар a) $n = 15$, б) $n = 16$ үед $1, 2,\dots, 2n - 1$ тоонуудыг байрлуулж
болох уу?
Заавар Бодолт
Заавар.
Бодолт. a) Хүснэгтийн багануудаа зүүнээс баруун $1, 2,\dots, 15$, мөрнүүдээ дээрээс доош $1, 2,\dots,
15$ гэж дугаарлая. Мөн $i$-р мөр, $j$-р баганы огтлолцолд бичигдсэн тоог $a_{ij}$ гэе. Мөн
$1 \le i \le 15$ үед $S_i = a_{1i} +a_{2i} +\dots+a_{15i} +a_{i1} +a_{i2} +\dots+a_{i15} -a_{ii}$ нийлбэрийг тэмдэглэе.
Энэ нийлбэрт $a_{ii}$ тоо нэг л удаа нэмэгдэнэ. $S_i$ бүр $1, 2,\dots, 29$ гэсэн тоонуудыг нэг удаа
агуулах бөгөөд $S_1, S_2,\dots, S_{15}$ гэсэн $15$ ширхэг нийлбэр байх тул $S_1 + S_2 + \dots + S_{15}$
нийлбэрт тоо бүр сондгой удаа байна. Нөгөө талаас $i\neq j$ байх $i$, $j$-ийн хувьд $a_{ij}$
элемент $S_i$, $S_j$ хоёуланд нь нэмэгдэнэ. Диагонал дээр бичигдэхгүй тоо $1, 2,\dots, 29$
дундаас олдох бөгөөд тэр тоо нийт нэмэгдэхүүнд тэгш удаа орох болж зөрчил үүснэ. Иймд болохгүй.
б) 8-р ангийн 4-р бодлоготой төстэйгээр байгуулагдана.
б) 8-р ангийн 4-р бодлоготой төстэйгээр байгуулагдана.
4. Ах, дүү 2 гэрээсээ сургууль руугаа зэрэг гарч дүү нь ахаасаа 39 минутын дараа сургууль дээрээ очив. Ахын хурдыг 40 хувиар багасгаж, дүүгийн
хурдыг 25 хувиар ихэсгэхэд тэд зэрэг сургууль дээрээ очиж чадах байв. Дүү сургууль руугаа хэдэн минут алхсан бэ?
Заавар Бодолт
Заавар.
Бодолт. Дүүгийн хурдыг $x$, ахын хурдыг $y$, сургууль болон гэр хоорондын замыг $S$ гэе. $x < y$
бөгөөд өгсөн нөхцөлүүдийг систем тэгшитгэл болгон бичвэл:
$$\left\{\begin{array}{c}
\dfrac{S}{y}+39=\dfrac{S}{x}\\
\dfrac{S}{0.6y}=\dfrac{S}{1.25x}
\end{array}\right.$$
болно. $0.6y = 1.25x$ гэдгээс $12y = 25x$ болно. Эхний нөхцөлийг хувиргавал
$$39=S\left(\dfrac1x-\dfrac1y\right)=S\left(\dfrac{y-x}{yx}\right)=S\cdot\dfrac{12y-12x}{12yx}=S\cdot\dfrac{13x}{25x^2}=\dfrac{13S}{25x}$$
болно. Эндээс $\dfrac{S}{x}=75$ минут болж дүүгийн гэр сургуулийн хооронд алхсан хугацаа нь гарч байна.
5. 1, 2 цифрээр бичигдэх 10 оронтой 99-д хуваагдах тоо хэд байх вэ?
Заавар Бодолт
Заавар.
Бодолт. 99-д хуваагдах 10 оронтой тоог $\overline{a_{10}a_9\dots a_1}$ гэж тэмдэглэе. Энэ тооны цифрүүдийн
нийлбэр 10-аас их 20-с бага бөгөөд 9-д хуваагдах тул 18 байна. Иймд 2 ширхэг 1, 8
ширхэг 2 цифрээс бүтсэн тоо байх ёстой болно. 11-д хуваагдах тооны шинжээр
$$a_{10} + a_8 + a_6 + a_4 + a_2 - a_9 - a_7 - a_5 - a_3 - a_1$$
илэрхийлэл 11-д хуваагдна. Энэ илэрхийллийн утга $5$-аас бага, $-5$-аас их байх учраас
0 байхаас өөрцгүй. Иймд сондгой (мөн тэгш) дугаартай цифрүүдийн аль нэг нь 1,
бусад нь 2 болно. Ингэж бичигдэх 10 оронтой тоо бүр 9 ба 11 тоонууд харилцан анхны
учир 99-д хуваагдана. Аль нэг сондгой (мөн тэгш) дугаартай цифрийг 1 гэж сонгох
боломж 5 учраас нийт 1, 2 цифрээр бичигдэх 10 оронтой 99-д хуваагдах тоонуудын
тоо 25 болно.
6. Дараалсан 2 тоо хөрш нүдэнд байхаар 2, 3, 4, 5, 6 гэсэн таван тоог дараах хүснэгтэд хэдэн янзаар нэмж бичиж болох вэ? Нэг нүдэнд нэгээс олон тоо бичихгүй.


Заавар Бодолт
Заавар.
Бодолт. Зүүн дээд булангаас хар, цагаанаар шатрын хөлөг шиг будсан гэе. Тэгвэл дараалсан тоонууд хөрш нүдэнд байх тул сондгой тоонууд ижил өнгөтэй нүдэнд, тэгш тоонууд ижил өнгөтэй нүдэнд байрлах болно. Эндээс 1 болон 6-ын тоо өөр өнгөтэй нүдэнд байрлах тул 6-ын тоо хар нүднүүдэд байрлаж чадахгүй бөгөөд зөвхөн цагаан нүдэнд байрлана.
 Одоо диагоналаас доош байрлах 6 нүдэнд 6 байрлах үед боломжийг тоолоод 2-оор
үржихэд бодлогын хариу гарна. Энэ боломжийг хялбархан
$$3 + 5 + 7 + 12 + 10 + 10 = 47$$
гэдгийг тоолж болох ба иймд нийт хариу 94 болно.
Одоо диагоналаас доош байрлах 6 нүдэнд 6 байрлах үед боломжийг тоолоод 2-оор
үржихэд бодлогын хариу гарна. Энэ боломжийг хялбархан
$$3 + 5 + 7 + 12 + 10 + 10 = 47$$
гэдгийг тоолж болох ба иймд нийт хариу 94 болно.
