IMO shortlist 2006 Монгол Бодлогын Сан

IMO shortlist 2006, 12-р анги

IMO-47, Словени

Бодлогын тоо: 30 Хугацаа: 540 мин

$a_0, a_1, a_2\dots$ бодит тоон дараалал

$a_{i+1}=\lfloor a_i\rfloor\cdot\langle a_i\rangle,\ i\ge0;$ ба

$a_0$ дурын бодит тоо гэж өгөгдөв. Энд

$\lfloor a_i\rfloor$ нь

$a_i$ тооноос хэтрэхгүй хамгийн их бүхэл тоо ба

$\langle a_i\rangle=a_i-\lfloor a_i\rfloor$ байг. Хангалттай их

$i$ тооны хувьд

$a_i=a_{i+2}$ болохыг батал.

$a_0, a_1, a_2,\dots$ бодит тоон дараалал

$a_0=-1, \quad \sum_{k=0}^n\dfrac{a_{n-k}}{k+1}=0, n\ge 1$ рекуррент томьёогоор өгөгдөв.

$n\ge 1$ үед

$a_n>0$ болохыг харуул.

$c_0, c_1, c_2,\dots,c_n,\dots$ дараалал

$c_0=1$ ,

$c_1=0$ ,

$c_{n+2}=c_{n+1}+c_n$ ,

$n\ge 0$ гэж тодорхойлогдов. Ямар нэг төгсгөлөг

$J$ олонлогийн хувьд

$x=\sum_{j\in J}c_j$ ,

$y=\sum_{j\in J}c_{j-1}$ байх бүх

$(x,y)$ эрэмбэлэгдсэн хосуудын олонлог

$S$ -ийг авч үзье. Дараах чанартай

$\alpha$ ,

$\beta$ ,

$m$ ,

$M$ бодит тоонууд оршин байхыг батал: Сөрөг биш бүхэл тоонуудын

$(x,y)$ эрэмбэлэгдсэн хосуудын хувьд

$m < \alpha x+\beta y < M$ байх зайлшгүй бөгөөд хүрэлцээтэй нөхцөл нь

$(x,y)\in S$ байна.

$a_1,\dots,a_n$ эерэг бодит тоонуудын хувьд

$\sum_{i < j}\dfrac{a_i a_j}{a_i+a_j}\le\dfrac{n}{2(a_1+a_2+\dots+a_n)}\sum_{i < j}a_ia_j$ тэнцэтгэл биш биелэхийг батал.

$a$ ,

$b$ ,

$c$ нь гурвалжны талууд байг.

$\dfrac{\sqrt{b+c-a}}{\sqrt{b}+\sqrt{c}-\sqrt{a}}+\dfrac{\sqrt{c+a-b}}{\sqrt{c}+\sqrt{a}-\sqrt{b}}+\dfrac{\sqrt{a+b-c}}{\sqrt{a}+\sqrt{b}-\sqrt{c}}\le 3$ болохыг батал.

6. Аливаа

$a$ ,

$b$ ,

$c$ бодит тоонуудын хувьд

$|ab(a^2-b^2)+bc(b^2-c^2)+ca(c^2-a^2)|\le M(a^2+b^2+c^2)^2$ тэнцэтгэл биш биелэх байх хамгийн бага бодит тоо

$M$ -г ол.

$L_1,\dots,L_n$ ,

$n\ge2$ чийдэнгүүд дараалж байрласан байв. Эдгээрийн зарим нь асаалттай, үлдсэн нь унтраастай байв. Секунд бүрд бид чийдэнгүүдийн төлвийг нэгэн зэрэг дараах дүрмээр өөрчилнө.

--- Хэрэв

$L_i$ ба түүний хөрш (

$i=1$ эсвэл

$i=n$ тохиолдолд 1 хөрш, бусад тохиолдод хоёр хөрштэй) чийдэнгүүд ижил төлөвт байвал

$L_i$ чийдэнг унтраана.

--- бусад тохиолдолд

$L_i$ чийдэнг асаана.

Эхлээд хамгийн зүүн талын чийдэн асаалттай бусад нь унтраастай байв.

Бүх чийдэнгүүд нэгэн зэрэг унтраастай төлөвт очих боломжтой $n$ төгсгөлгүй олон олдохыг батал.
Бүх чийдэнгүүд хэзээ ч нэгэн зэрэг унтраастай төлөвт очдоггүй $n$ төгсгөлгүй олон олдохыг батал.

Заавар Бодолт

Заавар.

Бага утгууд дээр шалгах замаар $n=2^k$ үед бүгд унтраастай байрлалд очихыг шалгаж болно.
$n=2^k+1$ үед бүгд унтрахгүй гэдгийг харуулахад хангалттай.

Бодолт.

8. Зөв

$2006$ өнцөгт

$P$ -ийн диагоналын төгсгөлийн цэгүүд нь

$P$ -ийн хилийг тус бүр сондгой тооны тал агуулах хоёр хэсэгт хувааж байвал түүнийг сайн гэе.

$P$ -ийн талуудыг мөн сайн гэе. Аль ч хоёр нь

$P$ -ийн дотор ерөнхий цэггүй байх

$2003$ диагоналаараа

$P$ гурвалжнуудад хуваагдсан байг. Тийм хуваалтад хоёр сайн талтай адил хажуут гурвалжин хамгийн олондоо хэд байж болох вэ?

Заавар Бодолт

Заавар. Consider a 2n-gon P. To simplify notation, draw the circumcircle of P. For a side AB in a triangle ABC, “arc AB” will denote the arc of the circumcircle not containing C. Arc AB is a “good arc” if AB is odd in a good triangle ABC.

Consider a side XY of P. Let AB denote the smallest good arc containing vertices X and Y, if it exists. (Note that {A, B} may be equal to {X, Y}.) Let C be the third vertex of the good triangle ABC. Then we will map XY to ABC: f(XY) = ABC.

Бодолт.

9. Хавтгайн төгсгөлөг цэгүүдээс тогтох

$S$ олонлогийн аль ч гурван цэг нь нэг шулуун дээр оршдоггүй байв. Оройнууд нь

$S$ олонлогийн элемент байх

$P$ гүдгэр олон өнцөгтийн хувьд

$a(P)$ нь оройн тоог,

$b(P)$ нь

$P$ олон өнцөгтийн гадна талд байрлах

$S$ -д харъяалагдах цэгийн тоог тэмдэглэж байв. Аливаа

$x$ бодит тооны хувьд

$\sum_{P}x^{a(P)}(1-x)^{b(P)}=1$ байхыг батал. Энд бүх оройнууд нь

$S$ олонлогийн элемент байх бүх

$P$ гүдгэр олон өнцөгтүүдээр нийлбэрчилж байна.

NB. Хэрчим, цэг, оройн хоосон олонлог нь харгалзан 2, 1, 0 оройтой гүдгэр олон өнцөгтүүд болохыг анхаар.

10.

$n^2$ ширхэг нэгж квадратаас тогтох

$n\times n$ квадрат хэлбэрийн бялуу байжээ. Түүний мөр ба багана бүрд яг нэг ширхэг гүзээлзгэнэ байрласан байв. Үүнийг

$\mathcal A$ байрлуулалт гэе.

$\mathcal B$ нь өөр нэгэн тийм байрлуулалт байв. Нэг орой нь бялууны зүүн дээд орой байдаг, өгөгдсөн нэгж квадратуудаас тогтох тэгш өнцөгт хэлбэртэй бялуу бүрийн хувьд

$\mathcal B$ байрлуулалт

$\mathcal A$ байрлуултаас цөөнгүй тооны гүзээлзгэнэтэй байг. Тэгвэл дараах үйлдлийн тусламжтайгаар

$\mathcal A$ байрлуулалтаас

$\mathcal B$ байрлуулалтад шилжиж чадахыг батал.

Нэг удаагийн үйлдэлээр зүүн доод ба баруун дээд буландаа л гүзээлзгэнэтэй аль нэг тэгш өнцөгтийг сонгоод гүзээлзгэнүүдийг нь нөгөө хоёр буланд нь шилжүүлж байрлуулна.

11.

$(n,k)$ тэмцээнд

$n$ тоглогч оролцож дараах байдлаар

$k$ тойрог үргэлжилнэ:

Тоглогч бүр бүх тойрогт тоглох бөгөөд аль ч хоёр тоглогч хамгийн олондоо нэг удаа хоорондоо тоглоно.
Хэрвээ $A$ тоглогч $B$ тоглогчтой $i$ -р тойрогт таарсан, $C$ тоглогч $D$ тоглогчтой $i$ -р тойрогт таарсан, мөн $A$ тоглогч $C$ тоглогчтой $j$ -р тойрогт таарсан бол $B$ тоглогч $D$ тоглогчтой $j$ -р тойрогт таарна.

$(n,k)$ тэмцээн оршин байх бүх

$(n,k)$ хосыг ол.

12. Талынх нь урт

$n$ -тэй тэнцүү, дээшээ чиглэсэн адил талт гурвалжинд

$n$ ширхэг мөн л дээшээ чиглэсэн, нэгж талтай зөв гурвалжин хэлбэрийн нүх гаргасан бол нүхлэгдсэн гурвалжин гэе. Алмаз нь

$60^\circ-120^\circ$ өнцгүүдтэй нэгж талтай ромбо юм.

$T$ нүхлэгдсэн гурвалжинг алмазаар хучиж болох зайлшгүй бөгөөд хүрэлцээтэй нөхцөл нь

$T$ доторх орших, талын урт нь

$k$ -тай тэнцүү аливаа зөв гурвалжин хамгийн олондоо

$k$ ширхэг нүхтэй байх явдал юм. Энд

$k$ нь

$1\le k\le n$ байна.

13. Аль ч хоёр ирмэг нь параллел биш, аль ч ирмэг нь хөрш талуудаасаа өөр параллел талсгүй гүдгэр олон талст авч үзье. Аливаа хоёр цэгийн хувьд тэдгээрийг агуулсан ямар нэг параллел хавтгайнуудын хооронд өгөгдсөн олон талст бүхлээрээ оршдог бол тэдгээрийг эсрэг байрлалтай цэгүүд гэе.

$A$ нь оройн цэгүүдээс тогтох эсрэг байрлалтай хосын тоо,

$B$ нь ирмэгүүдийн дундаж цэгүүдээс тогтох эсрэг байрлалтай хосын тоо бол

$A-B$ -г олон талстын оройн тоо, ирмэгийн тоо ба талсын тоогоор илэрхийл.

14.

$ABC$ гурвалжинд багтсан тойргийн төв

$I$ байг. Уг гурвалжин дотор

$P$ цэгийг

$\angle PBA+\angle PCA=\angle PBC+\angle PCB$ байхаар авав.

$AP\ge AI$ болохыг баталж, тэнцэл болох зайлшгүй бөгөөд хүрэлцээтэй нөхцөл нь

$P$ цэг

$I$ -тэй давхцах явдал гэж батал.

Заавар Бодолт

Заавар.

$\angle PBA+\angle PCA=\angle PBC+\angle PCB$ ба

$\begin{align*} \angle PBA&=\angle IBA-\angle IBP\\ \angle PCA&=\angle ICA+\angle ICP\\ \angle PBC&=\angle IBA+\angle IBC\\ \angle PCB&=\angle ICB-\angle ICP \end{align*}$ тул

$\angle IBA-\angle IBP+\angle ICA+\angle ICP=\angle IBA+\angle IBC+\angle ICB-\angle ICP$ болно.

$\angle IBA+\angle ICA=\angle IBC+\angle ICB$ болохыг тооцвол

$-\angle IBP+\angle ICP=\angle IBA-\angle ICP\Rightarrow \angle ICP=\angle IBP$ болно. Иймд

$P$ цэг

$BCI$ гурвалжныг багтаасан тойрог дээр байна.

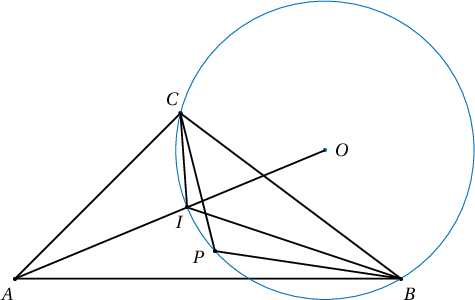
Бодолт. Одоо

$BCI$ гурвалжныг багтаасан тойргийн төв

$O$ нь

$AI$ цацраг дээр оршихыг батлахад хангалттай.

Комплекс хавтгайд

$A(a)$ ,

$B(b)$ ,

$C(c)$ ,

$I\equiv 0$ гэе.

$I$ биссектриссүүдийн огтлолцолын цэг тул

$\arg\dfrac{c-b}{0-b}=\arg\dfrac{0-b}{a-b},\ \arg\dfrac{b-c}{0-c}=\arg\dfrac{0-c}{a-c}$ буюу

$\dfrac{c-b}{0-b}:\dfrac{0-b}{a-b}\in\mathbb R, \dfrac{b-c}{0-c}:\dfrac{0-c}{a-c}\in\mathbb R$ болно. Эндээс

$\left\{\begin{array}{c} \dfrac{(c-b)(a-b)}{b^2}=\dfrac{(\overline{c\vphantom{b}}-\overline{b})(\overline{a\vphantom{b}}-\overline{b})}{\overline{b^2}}\\ \dfrac{(b-c)(a-c)}{c^2}=\dfrac{(\overline{b}-\overline{c\vphantom{b}})(\overline{a\vphantom{b}}-\overline{c\vphantom{b}})}{\overline{c^2}} \end{array} \right.$

$\left\{\begin{array}{c} \overline{b^2}(c-b)a-b^2(\overline{c\vphantom{b}}-\overline{b})\overline{a\vphantom{b}}=\overline{b^2}(c-b)b-b^2(\overline{c\vphantom{b}}-\overline{b})\overline{b}\\ \overline{c^2}(b-c)a-c^2(\overline{b}-\overline{c\vphantom{b}})\overline{a\vphantom{b}}=\overline{c^2}(b-c)c-c^2(\overline{b}-\overline{c\vphantom{b}})\overline{c\vphantom{b}} \end{array} \right.$

$\left\{\begin{array}{c} \overline{b^2}(c-b)a-b^2(\overline{c\vphantom{b}}-\overline{b})\overline{a\vphantom{b}}=b\overline{b}(\overline{b}c-b\overline{c\vphantom{b}})\\ \overline{c^2}(b-c)a-c^2(\overline{b}-\overline{c\vphantom{b}})\overline{a\vphantom{b}}=c\overline{c\vphantom{b}}(\overline{c\vphantom{b}}b-c\overline{b}) \end{array} \right.$

$\Rightarrow a=\dfrac{c^2b\overline{b}(\overline{b}c-b\overline{c\vphantom{b}})+b^2c\overline{c\vphantom{b}}(\overline{c\vphantom{b}}b-c\overline{b})}{c^2\overline{b^2}(c-b)+b^2\overline{c^2}(b-c)}=\dfrac{bc(c\overline{b}-b\overline{c\vphantom{b}})}{(c\overline{b}+b\overline{c\vphantom{b}})(c-b)}$

$BCI$ гурвалжныг багтаасан тойргийн төвийн координат нь

$z_0=\dfrac{0\overline{0}(b-c)+b\overline{b}(c-0)+c\overline{c\vphantom{b}}(0-b)}{\begin{vmatrix} 1 & 1 & 1\\ 0 & b & c\\ 0 & \overline{b} & \overline{c\vphantom{b}} \end{vmatrix}}=\dfrac{bc(\overline{b}-\overline{c\vphantom{b}})}{b\overline{c\vphantom{b}}-c\overline{b}}$

$A$ ,

$I$ ,

$O$ цэгүүд нэг шулуун дээр орших зайлшгүй бөгөөд хүрэлцээтэй нөхцөл нь

$\dfrac{a}{z_0}=\dfrac{\overline{a}}{\overline{z_0}}$ байна. Энэ нь

$\dfrac{a}{z_0}=\dfrac{\dfrac{bc(c\overline{b}-b\overline{c\vphantom{b}})}{(c\overline{b}+b\overline{c\vphantom{b}})(c-b)}}{\dfrac{bc(\overline{b}-\overline{c\vphantom{b}})}{b\overline{c\vphantom{b}}-c\overline{b}}}=\dfrac{(b\overline{c\vphantom{b}}-c\overline{b})^2}{(b\overline{c\vphantom{b}}+c\overline{b})(b-c)(\overline{b}-\overline{c\vphantom{b}})}$ ба

$\overline{b\overline{c\vphantom{b}}-c\overline{b}}=-(b\overline{c\vphantom{b}}-c\overline{b}),\ \overline{b\overline{c\vphantom{b}}+c\overline{b}}=b\overline{c\vphantom{b}}+c\overline{b},$

$\overline{(b-c)(\overline{b}-\overline{c\vphantom{b}})}=(\overline{b}-\overline{c\vphantom{b}})(b-c)$ гэдгээс батлах зүйл мөрдөн гарна.

15.

$ABCD$ нь сууриуд нь

$AB>CD$ нөхцөлийг хангах трапец байг.

$K$ ба

$L$ цэгүүд нь харгалзан

$AB$ ба

$CD$ хэрчмүүд дээр орших ба

$AK/KB=DL/LC$ нөхцөлийг хангана.

$P$ ба

$Q$ цэгүүд нь

$KL$ хэрчим дээр орших

$\angle APB=\angle BCD\text { ба }\angle CQD=\angle ABC$ нөхцөлийг хангадаг цэгүүд гэе. Тэгвэл

$P$ ,

$Q$ ,

$B$ ,

$C$ цэгүүд нэг тойрог дээр оршино гэж батал.

Заавар Бодолт

Заавар.

Бодолт.

16.

$ABCDE$ гүдгэр 5 өнцөгтийн хувьд

$\angle BAC=\angle CAD=\angle DAE\text{ ба }\angle ABC=\angle ACD=\angle ADE$ байв.

$BD$ ,

$CE$ диагоналууд

$P$ цэгт огтлолцдог. Тэгвэл

$AP$ шулуун

$CD$ хэрчмийг хагаслан хуваана гэж батал.

17.

$ABC$ гурвалжны

$\angle C<\angle A<90^\circ$ ба

$AC$ тал дээр нь

$BD=BA$ байхаар

$D$ цэг авав.

$ABC$ гурвалжинд багтсан тойрог

$AB$ ,

$AC$ талуудыг харгалзан

$K$ ба

$L$ цэгүүдэд шүргэнэ.

$J$ нь

$BCD$ гурвалжинд багтсан тойргийн төв.

$KL$ шулуун

$AJ$ хэрчмийг хагаслан хуваана гэж батал.

18.

$ABC$ гурвалжны хувьд

$J$ нь

$BC$ талыг

$A_1$ цэгт,

$AC$ ба

$AB$ талуудын үргэлжлэлийг харгалзан

$B_1$ ба

$C_1$ цэгт шүргэдэг гадаад багтсан тойргийн төв байг.

$A_1B_1$ ба

$AB$ шулуунууд перпендикуляр бөгөөд

$D$ цэг огтлолцдог гэе.

$E$ нь

$C_1$ цэгээс

$DJ$ шулуунд татсан перпендикуляр шулууны суурь.

$\angle BEA_1$ ба

$\angle AEB_1$ өнцгүүдийг ол.

19. Харгалзан

$O_1$ ба

$O_2$ төвтэй

$\omega_1$ ба

$\omega_2$ тойргууд

$D$ цэгт гадаад байдлаар шүргэлцэх бөгөөд

$\omega$ тойргийг харгалзан

$E$ ба

$F$ цэгт дотоод байдлаар шүргэнэ.

$t$ нь

$\omega_1$ ба

$\omega_2$ тойргуудыг

$D$ цэгт шүргэх ерөнхий шүргэгч шулуун.

$AB$ нь

$\omega$ тойргийн

$t$ шулуунд перпендикуляр диаметр ба

$A$ ,

$E$ ,

$O_1$ цэгүүд

$t$ шулууны нэг ижил талд оршино.

$AO_1$ ,

$BO_2$ ,

$EF$ ,

$t$ шулуунууд нэг цэгт огтлолцоно гэж батал.

20.

$ABC$ гурвалжны

$BC$ ,

$CA$ ,

$AB$ талуудын дундаж цэгүүд нь харгалзан

$M_a$ ,

$M_b$ ,

$M_c$ ;

$ABC$ -г багтаасан тойргийн

$BC$ ,

$CA$ ,

$AB$ нумуудын нөгөө оройг агуулаагүй нумын дундаж цэгүүд нь харгалзан

$T_a$ ,

$T_b$ ,

$T_c$ байв.

$i\in\{a,b,c\}$ индексүүдийн хувьд

$\omega_i$ нь

$M_iT_i$ диаметртэй тойргууд байв.

$p_i$ нь

$\omega_j$ ,

$\omega_k$ (

$\{i,j,k\}=\{a,b,c\}$ ) тойргуудын

$\omega_i$ нь

$\omega_j$ ,

$\omega_k$ -ийн эсрэг талд орших гадаад ерөнхий шүргэгч шулуун гэе.

$p_a$ ,

$p_b$ ,

$p_c$ шулуунууд

$ABC$ -тай төсөөтэй гурвалжин үүсгэхийг батал. Төсөөгийн коэффициентийг ол.

21.

$ABCD$ гүдгэр дөрвөн өнцөгт өгөгдөв.

$A$ ,

$D$ цэгүүдийг дайрсан тойрог

$B$ ,

$C$ цэгүүдийг дайрсан тойрогтой дөрвөн өнцөгтийн дотоод мужид орших

$P$ цэгт гадаад байдлаар шүргэлцэнэ.

$\angle PAB+\angle PDC\le 90^\circ\text{ ба }\angle PBA+\angle PCD\le 90^\circ$ гэе.

$AB+CD\ge BC+AD$ болохыг батал.

22.

$ABC$ гурвалжны

$BC$ ,

$CA$ ,

$AB$ талууд дээр харгалзан

$A_1$ ,

$B_1$ ,

$C_1$ цэгүүд авав.

$AB_1C_1$ ,

$BC_1A_1$ ,

$CA_1B_1$ гурвалжнуудыг багтаасан тойрог

$ABC$ гурвалжныг багтаасан тойрогтой харгалзан

$A_2$ ,

$B_2$ ,

$C_2$ цэгүүдэд

$(A_2\neq A, B_2\neq B, C_2\neq C)$ огтлолцоно.

$A_3$ ,

$B_3$ ,

$C_3$ нь харгалзан

$BC$ ,

$CA$ ,

$AB$ талуудын дундаж цэгүүдийн хувьд

$A_1$ ,

$B_1$ ,

$C_1$ цэгүүдтэй тэгш хэмтэй цэгүүд бол

$A_2B_2C_2$ гурвалжин

$A_3B_3C_3$ гурвалжинтай төсөөтэй гэдгийг батал.

23. Гүдгэр олон өнцөгт

$P$ -ийн

$b$ тал бүрд, нэг тал нь

$b$ -тэй давхцах

$P$ -д агуулагдах гурвалжнуудын талбайн хамгийн ихийг харгалзуулъя.

$P$ -ийн бүх талуудад харгалзах талбайнуудын нийлбэр,

$P$ -ийн талбайг хоёр дахин авснаас багагүй гэж батал.

24.

$1+2^x+2^{2x+1}=y^2$ байх бүхэл тооны бүх хос

$(x,y)$ -г ол.

25.

$x\in(0,1)$ тооны хувьд

$y\in(0,1)$ тооны таслалаас хойших

$n$ дэх цифр нь

$x$ тооны таслалаас хойших

$(2^n)$ дэх цифртэй тэнцүү. Хэрвээ

$x$ рационал тоо бол

$y$ ч мөн адил рационал тоо гэж харуул.

26.

$f(1),\ f(2),\ f(3),\dots$ дараалал

$f(n) = \dfrac{1}{n}\left(\left\lfloor\dfrac{n}{1}\right\rfloor+\left\lfloor\dfrac{n}{2}\right\rfloor+\dots+\left\lfloor\dfrac{n}{n}\right\rfloor\right)$ гэж тодорхойлогдов. Энд

$\lfloor x\rfloor$ нь

$x$ тоон бүхэл хэсэг юм.

(a)

$f(n + 1) > f(n)$ төгсгөлгүй олон тохиолдохыг батал.

(b)

$f(n + 1) < f(n)$ төгсгөлгүй олон тохиолдохыг батал.

27.

$P(x)$ бүхэл коэффициенттэй

$n>1$ зэргийн олон гишүүнт ба

$k$ нь натурал тоо байг.

$Q(x) = P(P(\ldots P(P(x))\ldots))$ олон гишүүнт авъя (энд

$P$ яг

$k$ удаа орсон).

$Q(t)=t$ байх

$t$ бүхэл тоо

$n$ -ээс илүүгүй оршин байхыг батал.

28.

$\dfrac{x^7-1}{x-1}=y^5 - 1$ тэгшитгэлийн бүх бүхэл шийдийг ол.

29.

$a > b > 1$ нь өгөгдсөн харилцан анхны натурал тоонууд.

$ax + by = c$ байх бүх боломжит

$x$ ,

$y$ бүхэл тоонуудаар зохиогдох

$|x| + |y|$ нийлбэрийн авч болох хамгийн бага утгыг

$c$ бүхэл тооны жин гээд

$w(c)$ гэж тэмдэглэе. Хэрвээ

$w(c) \ge w(c \pm a)$ ба

$w(c) \ge w(c \pm b)$ биелдэг бол

$c$ тоог хэсгийн аварга гэе. Бүх хэсгийн аваргууд болон тэдгээрийн тоог ол.

30. Натурал тоо

$n$ бүрийн хувьд

$2^m+m$ тоо

$n$ -д хуваагддаг байхаар

$m$ бүхэл тоо олдохыг батал.

IMO shortlist 2006, 12-р анги

Санал хүсэлт: