ММО-24, 10-р анги
Бодлогын тоо: 6 Хугацаа: 540 мин
1. $$\left\{\begin{array}{c}
x^3-y^3-z^3=3xyz\\
x^2=4(y+z)
\end{array}\right.$$
системийн бүх сөрөг биш, бүхэл шийдийг ол.
Заавар Бодолт
Заавар.
Бодолт. $x=0$ бол $y=-z$ ба хоёул эерэг тул $(0,0,0)$ байна.
$x>0$ бол $x^3\geqslant 3xy\Rightarrow x^2\geqslant 3yz$ тул $$3yz\leqslant 4(y+z)$$ болно. $y\leqslant z$ гэж үзье. Тэгвэл $3yz\leqslant 8z$ тул $y\leqslant \dfrac{8}{3}$ байна. Иймд $y=0,1,2$ байх боломжтой.
$y=0$ бол $x^3=z^3\Rightarrow x=z$ ба $x^2=4x\Rightarrow x=4$ тул $(x,y,z)=(4,0,4)$.
$y=1$ бол $\left\{\begin{array}{c} x^3-z^3=3xz+1\\ x^2=4(1+z) \end{array}\right.$ болно. $$x^3-z^3-3xz-1=(x - z - 1) (x^2 + x z + x + z^2 - z + 1)=0$$ ба $$x^2 + x z + x + z^2 - z + 1\geqslant z^2-z+1>0$$ тул $x=z+1$ болно. Иймд $(z+1)^2=4(1+z)$ ба $z+1\neq 0$ тул $z=3$, $x=4$.
$y=2$ бол $\left\{\begin{array}{c} x^3-z^3=6xz+8\\ x^2=4(2+z) \end{array}\right.$ болно. $$x^3-z^3-6xz-8=(x - z - 2) (x^2 + x z + 2 x + z^2 - 2 z + 4)=0$$ ба $$x^2 + x z + 2 x + z^2 - 2 z + 4\geqslant z^2-2z+4>0$$ тул $x=z+2$ болно. Иймд $(z+2)^2=4(2+z)$ ба $z+2\neq 0$ тул $z=2$, $x=4$.
Хариу: $(x,y,z)=(0,0,0)\lor (4,0,4)\lor (4,4,0)\lor (4,1,3)\lor (4,3,1)\lor (4,2,2)$
$x>0$ бол $x^3\geqslant 3xy\Rightarrow x^2\geqslant 3yz$ тул $$3yz\leqslant 4(y+z)$$ болно. $y\leqslant z$ гэж үзье. Тэгвэл $3yz\leqslant 8z$ тул $y\leqslant \dfrac{8}{3}$ байна. Иймд $y=0,1,2$ байх боломжтой.
$y=0$ бол $x^3=z^3\Rightarrow x=z$ ба $x^2=4x\Rightarrow x=4$ тул $(x,y,z)=(4,0,4)$.
$y=1$ бол $\left\{\begin{array}{c} x^3-z^3=3xz+1\\ x^2=4(1+z) \end{array}\right.$ болно. $$x^3-z^3-3xz-1=(x - z - 1) (x^2 + x z + x + z^2 - z + 1)=0$$ ба $$x^2 + x z + x + z^2 - z + 1\geqslant z^2-z+1>0$$ тул $x=z+1$ болно. Иймд $(z+1)^2=4(1+z)$ ба $z+1\neq 0$ тул $z=3$, $x=4$.
$y=2$ бол $\left\{\begin{array}{c} x^3-z^3=6xz+8\\ x^2=4(2+z) \end{array}\right.$ болно. $$x^3-z^3-6xz-8=(x - z - 2) (x^2 + x z + 2 x + z^2 - 2 z + 4)=0$$ ба $$x^2 + x z + 2 x + z^2 - 2 z + 4\geqslant z^2-2z+4>0$$ тул $x=z+2$ болно. Иймд $(z+2)^2=4(2+z)$ ба $z+2\neq 0$ тул $z=2$, $x=4$.
Хариу: $(x,y,z)=(0,0,0)\lor (4,0,4)\lor (4,4,0)\lor (4,1,3)\lor (4,3,1)\lor (4,2,2)$
2. Хавтгай дээр тойрог ба $A$ цэг өгөгджээ. $A$ цэгийг дайрсан огтлогчийн тойрогтой огтлолцсон цэгүүдэд татсан шүргэгчүүдийн огтлолцлын геометр байрыг ол.
3. Хавтгай дээр ерөнхий байршилтай $2n$ ($n\ge 4$) ширхэг цэг өгөгджээ. Аль ч цэг нь яг нэг хэрчмийн үзүүр байхаар эдгээр цэгийг $n$ ширхэг хэрчмээр, бүх хэрчмийг нэг шулуунаар огтолж а) болдог б) болдоггүй байхаар холбож болохыг тус тус батал.
Заавар Бодолт
Заавар.
Бодолт. а) Ерөнхий байршилтай цэгүүд тул эдгээр цэгүүдийн алийг нь ч дайраагүй, хоёр талд нь $n$, $n$ цэг байрлаж байхаар шулуун татаж болно. Хэсэг тус бүрээс 1, 1 цэг аваад хэрчмээр холбоход үүсэх $n$ хэрчим бодлогын нөхцөлийг хангах нь ойлгомжтой.
б) $n=4$ үед л батлахад хангалттай. Дурын 5 цэгээс гүдгэр 4 өнцөгтийн орой болох 4 цэг сонгож болдог. Иймд өгөгдсөн цэгүүдэд оройтой ямар нэг гүдгэр 4 өнцөгт олдоно. Дөрвөн өнцөгт дотор орших цэг нь дөрвөн өнцөгтийн аль нэг гурван оройн хамт өөр нэг гүдгэр дөрвөн өнцөгтийн орой болж чадна. Иймд бид дотроо өгөгдсөн цэгүүдээс нэгийг нь ч агуулаагүй гүдгэр 4 өнцөгт сонгон авч болно. Уг гүдгэр 4 өнцөгтийг $ABCD$ гээд $AC$, $BD$ шулуунаар хавтгайг 4 хэсэгт хуваая.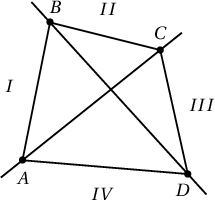
$I$, $II$, $III$, $IV$ хэсгүүдийн аль нэгд нь үлдэх 4 цэгээс хоёр нь ордог байг. Уг хоёр цэг $I$ хэсэгт байдаг гэж үзэхэд явцуурахгүй. Энэ тохиолдолд $ABCD$ дотор өөр цэг байх боломжгүй тул уг хоёр цэгийг холбосон хэрчим болон $AD$, $BC$ хэрчмийг нэгэн зэрэг огтлох шулуун олдохгүй.
Эсрэг тохиолдолд хэсэг тус бүрд нэг, нэг цэг байна. $I$ хэсэгт харъяалагдах цэгийг $E$, $II$ хэсэгт харъяалагдах цэгийг $F$, $III$ хэсэгт харъяалагдах цэгийг $G$, $IV$ хэсэгт харъяалагдах цэгийг $H$ гэе. Тэгвэл $AE$, $BF$, $CG$, $DH$ хэрчмүүдийг нэгэн зэрэг огтлох шулуун олдохгүй. Учир нь ямар ч шулуун огтлолцсон хоёр шулуунаар үүсэх 4 хэсгийг бүгдийг нь дайрахгүй.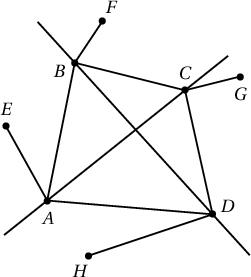
б) $n=4$ үед л батлахад хангалттай. Дурын 5 цэгээс гүдгэр 4 өнцөгтийн орой болох 4 цэг сонгож болдог. Иймд өгөгдсөн цэгүүдэд оройтой ямар нэг гүдгэр 4 өнцөгт олдоно. Дөрвөн өнцөгт дотор орших цэг нь дөрвөн өнцөгтийн аль нэг гурван оройн хамт өөр нэг гүдгэр дөрвөн өнцөгтийн орой болж чадна. Иймд бид дотроо өгөгдсөн цэгүүдээс нэгийг нь ч агуулаагүй гүдгэр 4 өнцөгт сонгон авч болно. Уг гүдгэр 4 өнцөгтийг $ABCD$ гээд $AC$, $BD$ шулуунаар хавтгайг 4 хэсэгт хуваая.
Эсрэг тохиолдолд хэсэг тус бүрд нэг, нэг цэг байна. $I$ хэсэгт харъяалагдах цэгийг $E$, $II$ хэсэгт харъяалагдах цэгийг $F$, $III$ хэсэгт харъяалагдах цэгийг $G$, $IV$ хэсэгт харъяалагдах цэгийг $H$ гэе. Тэгвэл $AE$, $BF$, $CG$, $DH$ хэрчмүүдийг нэгэн зэрэг огтлох шулуун олдохгүй. Учир нь ямар ч шулуун огтлолцсон хоёр шулуунаар үүсэх 4 хэсгийг бүгдийг нь дайрахгүй.
4. $x_1=4$, $x_{n+1}=7x_n+4\sqrt{3x_n^2+1}$ $(n\ge 1)$ дарааллын гишүүн бүр тэгш натурал тоо байхыг батал.
Заавар Бодолт
Заавар.
Бодолт. Өгөгдсөн рекуррент томьёоноос
$$(x_{n+1}-7x_n)^2=48x_n^2+16$$
буюу
$$x_{n+1}^2-14 x_{n+1}x_n +x_n^2-16=0$$
байна. Иймд
$$x_n^2-14 x_nx_{n-1} +x_{n-1}^2-16=0,\quad n\geqslant 2$$
байна. Эдгээрийг хасвал
$$(x_{n+1}^2-x_{n-1}^2)-14x_n(x_{n+1}-x_{n-1})=0$$
буюу
$$(x_{n+1}-x_{n-1})(x_{n+1}-14x_n+x_{n-1})=0$$
болно. $x_n$ дараалал эрс өсдөг дараалал гэдэг нь илт тул
$$x_{n+1}=14x_n-x_{n-1}$$
рекуррент томьёо биелнэ.
$$x_2=7\cdot 4+16\sqrt{3\cdot 4^2+1}=140$$
тул бүх гишүүд нь тэгш натурал тоо болно.
5. $ABC$ гурвалжны $AB$, $BC$ талууд дээр $\angle BCN=\dfrac13\angle BCA$, $\angle BAM=\dfrac13\angle BAC$ байхаар $N$ ба $M$ цэгийг сонгон авчээ. Хэрэв $CN=AM$ бол $ABC$ гурвалжин адил хажуут гэж батал.
6. $5^n$ ($n\ge 1$) радиустай тойрог дээр аль ч хоёрын нь хоорондох зай бүхэл байхаар $n+1$ ширхэг цэг сонгон авч болохыг батал.
Заавар Бодолт
Заавар.
Бодолт. $R$ радиустай тойрог дээр байрлах $\alpha$ төв өнцгийн төгсгөлийн хоёр цэгийн хоорондох зай $d=2R\sin(\alpha/2)$ байдгийг саная.
$\cos\varphi=\dfrac{3}{5}$, $\sin\varphi=\dfrac{4}{5}$ байх $\varphi$ өнцөг авъя. Тэгвэл Муаврын томьёогоор $$\cos m\varphi+i\sin m\varphi=\left(\dfrac{3}{5}+\dfrac{4}{5}i\right)^m$$ тул $$\sin m\varphi=\sum_{k=0}^{[m/2]}(-1)^k\binom{m}{2k+1}\dfrac{3^{m-2k-1}\cdot 4^{2k+1}}{5^m}$$ байна. $R=5^n$ радиустай тойрог дээр $A_k=\big(R\cos (2\varphi k), R\sin (2\varphi k)\big)$, $k=\overline{0,n}$ гэсэн $n+1$ ширхэг цэг авъя. Тэгвэл $0\leqslant i < j\leqslant n$ байх $A_i$, $A_j$ цэгүүдийн хоорондох зай $$|A_iA_j|=2\cdot 5^n\sin(j-i)\varphi=2\cdot 5^{n-m}\sum_{k=0}^{[(j-i)/2]}(-1)^k\binom{m}{2k+1}3^{m-2k-1}\cdot 4^{2k+1}\in\mathbb Z$$ тул аль ч хоёрынх нь хоорондох зай бүхэл байна.
$\cos\varphi=\dfrac{3}{5}$, $\sin\varphi=\dfrac{4}{5}$ байх $\varphi$ өнцөг авъя. Тэгвэл Муаврын томьёогоор $$\cos m\varphi+i\sin m\varphi=\left(\dfrac{3}{5}+\dfrac{4}{5}i\right)^m$$ тул $$\sin m\varphi=\sum_{k=0}^{[m/2]}(-1)^k\binom{m}{2k+1}\dfrac{3^{m-2k-1}\cdot 4^{2k+1}}{5^m}$$ байна. $R=5^n$ радиустай тойрог дээр $A_k=\big(R\cos (2\varphi k), R\sin (2\varphi k)\big)$, $k=\overline{0,n}$ гэсэн $n+1$ ширхэг цэг авъя. Тэгвэл $0\leqslant i < j\leqslant n$ байх $A_i$, $A_j$ цэгүүдийн хоорондох зай $$|A_iA_j|=2\cdot 5^n\sin(j-i)\varphi=2\cdot 5^{n-m}\sum_{k=0}^{[(j-i)/2]}(-1)^k\binom{m}{2k+1}3^{m-2k-1}\cdot 4^{2k+1}\in\mathbb Z$$ тул аль ч хоёрынх нь хоорондох зай бүхэл байна.