Монгол Бодлогын Сан

Заавар: Гурван шулуун нэг цэгээр огтлолцох зайлшгүй бөгөөд хүрэлцээтэй нөхцөл нь хоёрынх нь огтлолцлын цэг гурав дахь шулуун дээр орших.

Бодолт: $\triangle ABC$-ийн өндрүүдийг $AL$, $BM$, $CN$ гэе. Түүнчлэн $BC$ тал $x$ тэнхлэг дээр, $A$ цэг $y$ тэнхлэг дээр байхаар координатын системийг сонгоё. Тэгвэл $A(0, a)$, $B(b, 0)$, $C(c, 0)$ ба $a\ne0$, $b\ne c$ болно. $b=0$ эсвэл $c=0$ бол $\triangle ABC$ нь тэгш өнцөгт гурвалжин байх тул гурван өндөр нь нэг цэгээр огтлолцоно. Иймд $b\ne 0$ ба $c\ne 0$ гэе. $CA$, $AB$ шулуунуудын өнцгийн коэффициент нь харгалзан $-a/c$, $-a/b$ болох бөгөөд тэдгээрт перпендикуляр $BM$, $CN$ шулуунуудын тэгшитгэл нь $$BM: y=\dfrac ca(x-b),     CN: y=\dfrac ba(x-c)$$ болно. $BM$, $CN$ шулуунуудын огтлолцлын цэгийн координат нь $$H\left(0,-\dfrac{bc}{a}\right)$$ болох тул энэ цэг нь $AL$ шулуун дээр байна.

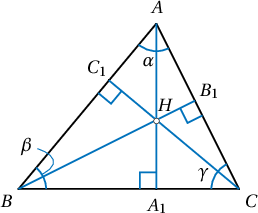
Заавар: Өндрүүдийг $AA_1$, $BB_1$, $CC_1$ гэвэл $AC_1=AC\cos\alpha$, $C_1B=BC\cos\beta$, $BA_1=AB\cos\beta$, $A_1C=CA\cos\gamma$, $CB_1=BC\cos\gamma$, $B_1A=AB\cos\alpha$ гэдгээс $$\dfrac{AC_1}{C_1B}\cdot\dfrac{BA_1}{A_1C}\cdot\dfrac{CB_1}{B_1A}=\dfrac{AC\cos\alpha}{BC\cos\beta}\cdot\dfrac{AB\cos\beta}{CA\cos\gamma}\cdot\dfrac{BC\cos\gamma}{AB\cos\alpha}=1$$ тул Чевийн теоремоор нэг цэгт огтлолцоно.

Бодолт: