Монгол Бодлогын Сан

Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.

$\cos 36^{\circ}$ -ийн утгыг дараах хоёр аргаар ол.

Бодлогын төрөл: Уламжлалт

Заавар:

Бодолт:

$\theta=36^{\circ}$ гэвэл $3\theta=180^{\circ}-2\theta\Rightarrow\sin 3\theta=\sin (180^{\circ}-2\theta)\Rightarrow\sin 3\theta=\sin2\theta$ байна. Давхар өнцгийг дан өнцгөөр илэрхийлбэл $-4\sin^3\theta+3\sin \theta=2\sin \theta\cdot \cos \theta\Rightarrow \sin\theta\cdot(-4\sin^2\theta+3-2\cos \theta)=0$ $\sin 36^{\circ}\ne 0$ тул $-4\sin^2\theta+3-2\cos \theta=4(\cos^2\theta-1)+3-2\cos\theta=0\Rightarrow 4c^2-2c-1=0.$ Нөгөө талаас $0< \cos \theta< 1$ тул $\cos\theta=\dfrac{1+\sqrt{5}}{4}$ .
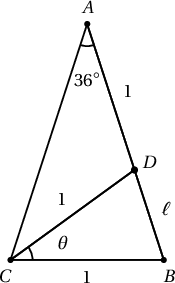
Оройн $\measuredangle A=36^{\circ} \Rightarrow$ суурийн өнцөг нь $72^{\circ}$ ба $\theta=36^{\circ}$ .
Зургаас харвал $\triangle CBD \sim \triangle ABC$ тул $\dfrac{BD}{BC}=\dfrac{BC}{BA}$ болох ба $BC=1$ , $BD=\ell$ гэвэл $\dfrac {\ell}1=\dfrac1{\ell+1}$ -ийг бодож $\ell$ -ийг олбол: $\ell=\dfrac{-1+\sqrt{5}}{2}$ , $\triangle CBD$ гурвалжны хувьд косинусийн теорем бичиж $\cos\theta$ -ийг олбол: $\cos \theta=\dfrac{1^2+1^2-\ell^2}{2\cdot 1\cdot 1}=\dfrac{1+\sqrt{5}}{4}.$