Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Тригонометрийн хялбар тэгшитгэлүүд, ерөнхий шийд
$0^{\circ}\leq \theta< 360^{\circ}$ байх шийдүүд ба ерөнхий шийдийг ол.
- $\sin\theta=\dfrac 12$
- $\cos\theta=-\dfrac{\sqrt{3}}2$
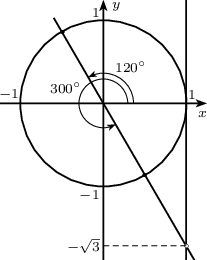
- $\tg\theta=-\sqrt{3}$
Бодлогын төрөл: Уламжлалт
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Тригонометр тэгшитгэл. $\sin\theta=q$,
$\cos\theta=p$, $\tg\theta=t$ тэгшитгэлүүдийн шийдийг олохын тулд тодорхойлолтын дагуу
- $\theta$-өнцгийг зурах хэрэгтэй. $\theta$ өнцгийг зурахын тулд $y=q$, $x=p$ шулуунуудын нэгж тойрогтой огтлолцох цэгүүдийг ($P$-цэг) олно. $y=t$ шулуун ба $x=1$ шулуунуудын огтлолцлын цэгийг $T$ гэе. $OT$ шулууны нэгж тойрогтой огтлолцох цэгийг ($P$-цэг) олно.
- $\measuredangle POX$ өнцгийн хэмжээг олно. Олсон шийдийн хувьд ерөнхий шийдийг бич.
- $\tg\theta=t$-ийн ерөнхий шийд нь $\theta+\pi\cdot k$ хэлбэртэй байна.
Бодолт:
- Нэгж тойргийн $y=\frac12$ шулуунтай огтлолцох цэгүүд нь $\big(-\frac{\sqrt3}2,\frac12\big)$, $\big(\frac{\sqrt3}2,\frac12\big)$ ба харгалзах өнцгүүд нь $150^\circ$, $30^\circ$ байна. $150^\circ\equiv\dfrac{5\pi}{6}$, $30^\circ\equiv\dfrac{\pi}{6}$ тул ерөнхий шийд нь $\theta=\dfrac{\pi}{6}+2\pi k$, $\dfrac{5\pi}{6}+2\pi k$ байна. Үүнийг бүр ерөнхий байдлаар $\theta=(-1)^k\dfrac{\pi}{6}+\pi k$ гэж бичиж болдог.

- Нэгж тойргийн $x=-\frac{\sqrt3}2$ шулуунтай огтлолцох цэгүүд нь $\big(-\frac{\sqrt3}2,\frac12\big)$, $\big(-\frac{\sqrt3}2,-\frac12\big)$ ба харгалзах өнцгүүд нь $150^\circ$, $210^\circ (-150^\circ)$ байна. $150^\circ\equiv\dfrac{5\pi}{6}$, $210^\circ\equiv-\dfrac{5\pi}{6}$ тул ерөнхий шийд нь $\theta=\pm\dfrac{5\pi}{6}+2\pi k$ байна.

- Координатын эх ба $(1,-\sqrt3)$ цэгийг дайрсан шулуун нь нэгж тойргийг $\big(-\frac12,\frac{\sqrt3}2\big)$, $\big(\frac12,-\frac{\sqrt3}2\big)$ цэгүүдэд огтлох ба харгалзах өнцгүүд нь $120^\circ$, $300^\circ$ байна. $120^\circ\equiv\dfrac{2\pi}{3}$ тул ерөнхий шийд нь $\theta=\dfrac{2\pi}{3}+\pi k$ байна.