Монгол Бодлогын Сан

Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.

Координатын хавтгайд $O(0, 0)$ , $A(1, 3)$ , $B(5, 6)$ , $C(-2, 7)$ , $D(t, 0) [t>0]$ цэгүүд өгөгдөв.

Бодлогын төрөл: Уламжлалт

Заавар: Координатын хавтгайн

$A(x_1,y_1), B(x_2,y_2)$ цэгүүдийн хоорондох зай нь

$AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$ .

$\triangle ABC$ -ийн хувьд

$AB^2+AC^2=BC^2$ бол

$\angle A=90^\circ$ байна.

$(3)$ -ийн хувьд

$\triangle ABD$ адил хажуут бол

$DA=DB, AD=AB, BA=BD$ гэсэн гурван боломж бий.

Бодолт:

$OA=\sqrt{1^2+3^2}=\sqrt{10}$

$AB=\sqrt{(5-1)^2+(6-3)^2}=\sqrt{25}=5$
$AC=\sqrt{(-2-1)^2+(7-3)^2}=\sqrt{25}=5$

$BC=\sqrt{(-2-5)^2+(7-6)^2}=\sqrt{50}=5\sqrt{2}$ тул

$AB^2+AC^2=BC^2$ буюу $\angle A=90^\circ$
$DA=DB$ бол $DA^2=(1-t)^2+3^2=t^2-2t+10$
$DB^2=(5-t)^2+6^2=t^2-10t+61$

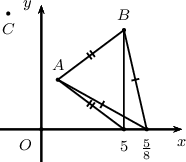
$DA^2=DB^2$ гэдгээс $t^2-2t+10=t^2-10t+61,t=\dfrac{51}{8}$

$AD=AB$ бол өмнөхтэй ижилээр $t^2-2t-15=0$ , $t=5$ , $t=-3$ . $t>0$ гэдгээс $t=5$ .

$BA=BD$ бол $t^2-10t+36=0$ , $D/4=5^2-36=-11< 0$ тул ийм байх боломжгүй. $t=\dfrac{51}{8},5$