Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Гүдгэр мужид функцийн ХИ, ХБ утга олох
$x, y$ нь $x^2+y^2\leq 10$, $y\geq -2x+5$ нөхцлийг хангах үед $x+y$-ийн хамгийн их утга $\fbox{a}\sqrt{\fbox{b}}$ ба хамгийн бага утга $\fbox{c}$ байна.
ab = 25
c = 2
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 34.29%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: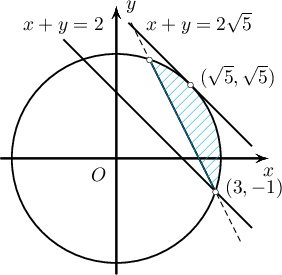 
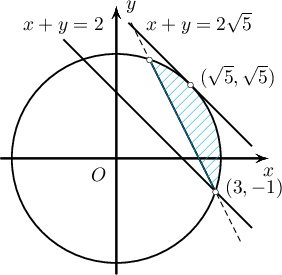
Бодолт: $x^2+y^2=10 \boldsymbol{\cdots} (1)$, $y=-2x+5 \boldsymbol{\cdots} (2)$
гэвэл (1), (2)-ийн огтлолцлын цэг $Q(1, 3), P(3,-1)$ байна.
$x^2+y^2\leq 10, y\geq -2x+5$ нөхцөл хангах цэгүүдийн олонлогийг $D$ гэвэл $D$ нь тойргийн сегмент байна.
$x+y=k \boldsymbol{\cdots}(3)$ гэвэл (3) нь өнцгийн коэффициент нь $-1$ байх шулуун юм. (1) ба (3) ерөнхий цэгтэй байхын тулд $\dfrac{|0+0-k|}{\sqrt{1^2+1^2}}\leq \sqrt{10}$ байх ёстой. Иймд $|k|\leq 2\sqrt{5}$ ба $|k|=2\sqrt{5}$ үед шүргэнэ.
$k=2\sqrt{5}$ үед $(1)$ ба $(3)$ нь I мөчид $(\sqrt{5},\sqrt{5})$ цэгээр шүргэлцэнэ. $k$ ихэсэхэд (3) шулуун баруун дээшээ шилжих тул $3+(-1)\leq k\leq
\sqrt{5}+\sqrt{5}$ байна. Эндээс $2\leq x+y\leq 2\sqrt{5}$ болно.