Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Квадрат тэгшитгэлийн шийдийн байршил
$x^2-2(k+1)x+2(k^2+3k-10)=0$ тэгшитгэлийн шийдүүд нь эерэг байх $k$ параметрийн утгын мужийг ол.
Бодлогын төрөл: Уламжлалт
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $f(x)=ax^2+bx+c$-ийн хувьд $a>0$, $D=b^2-4ac$ ба оройн цэгийн абсцисс нь $x_0=-\frac{b}{2a}$ байг. $f(x)=0$ квадрат тэгшитгэлийн шийдүүд $\alpha <\beta$ ба $R\in\mathbb R$ бол
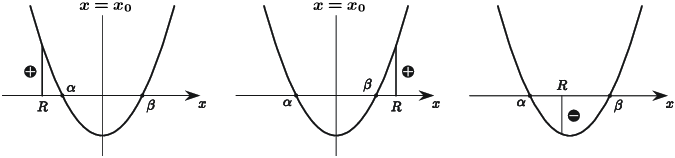байна.
- $R< \alpha, \beta\Leftrightarrow 0\le D$, $0< f(R)$, $R< x_0$;
- $\alpha, \beta< R\Leftrightarrow 0\le D$, $0< f(R)$, $x_0< R$;
- $\alpha< R< \beta\Leftrightarrow f(R)< 0$
Бодолт: $R=0$ тул заавар ёсоор $D\geq 0$, $x_0>0$, $f(0)>0$ болно. Мөн $x_0=k+1$ байна.
- $D\geq 0$ тул $D=4(k+1)^2-8(k^2+3k-10)\geq 0$ буюу $-7\leq k\leq 3$;
- $x_0=-\dfrac{-2(k+1)}{2}=k+1>0$ буюу $k\geq -1$;
- $f(0)>0$ буюу $2(k^2+3k-10)>0$ тул $k< -5\lor k>2$.
Сорилго
Японы ном, Квадрат тэгшитгэлийн шийдийн байршил
Алгебрийн тэгшитгэл - Квадрат тэгшитгэл
Квадрат Тэгшитгэл, Тэнцэтгэл биш 2022-2023 хичээлийн жил