Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Бодлого №10228
Дараах шугамуудаар хүрээлэгдсэн дүрсийн талбайг ол.
- $y=x^3-3x^2$, $x$ тэнхлэг
- $y=x^4-4x^2, y=x^2-4$
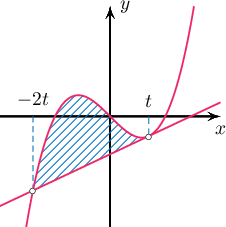
- $C: y=x^3-x$, $C$ муруйн $P$ цэг дээрх шүргэгч.
Бодлогын төрөл: Уламжлалт
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар:
Бодолт:
- $y=x^3-3x^2$ ба $x$ тэнхлэгийн огтлолцлын цэгүүд нь $x^3-3x^2=0\Rightarrow x_1=0$, $x_2=3$. Иймд \begin{align*} S&=-\int_0^3x(x-3)^2dx=-\left.x\cdot\dfrac{(x-3)^3}{3}\right|_0^3+\int_0^3\dfrac{(x-3)^3}{3}dx\\ &=-\left.\dfrac{x(x-3)^3}{3}\right|_0^3+\left.\dfrac{(x-3)^4}{12}\right|_0^3=\dfrac{27}{4}\\ \end{align*}
- $y=x^4-4x^2, y=x^2-4$ муруйнуудын огтлолцлын цэгүүд нь $x^4-4x^2=x^2-4 \Rightarrow x_1=-2$, $x_2=-1$, $x_3=1$, $x_4=2$ байна. Иймд \begin{align*} S&=-\int_{-2}^{-1}(x^4-5x^2+4)\,dx+\int_{-1}^{1}(x^4-5x^2+4)\,dx-\int_{1}^{2}(x^4-5x^2+4)\,dx\\ &=-\left(\dfrac{x^5}{5}-\dfrac{5x^3}{3}+4x\right)\Bigg|_{-2}^{-1}+\left(\dfrac{x^5}{5}-\dfrac{5x^3}{3}+4x\right)\Bigg|_{-1}^{\phantom{-}1}-\left(\dfrac{x^5}{5}-\dfrac{5x^3}{3}+4x\right)\Bigg|_{1}^{2}\\ &=\dfrac{22}{15}+\dfrac{76}{15}+\dfrac{22}{15}=\dfrac{120}{15}=8 \end{align*}
- $C: y=x^3-x$, $C$ муруйн $P(t,t^3-t)$ цэг дээрх шүргэгч шулууны тэгшитгэл
\[
y=(3t^2-1)(x-t)+t^3-t
\]
байна.
\[
x^3-x=(3t^2-1)(x-t)+t^3-t\Rightarrow (x+2t)(x-t)^2=0
\]
тул шүргэгч шулуун $C$-тэй $P$-ээс гадна $Q(-2t, -8t^3+2t)$ цэгт огтлолцоно. $t > 0$ гэвэл
\begin{align*}
S&=\int_{-2t}^t(x+2t)(x-t)^2\,dt=(x+2t)\cdot\dfrac{(x-t)^3}{4}\Bigg|_{-2t}^{\phantom{-2}t}-\int_{-2t}^t\dfrac{(x-t)^3}{3}dt\\
&=(x+2t)\cdot\dfrac{(x-t)^3}{4}\Bigg|_{-2t}^{\phantom{-2}t}-\dfrac{(x-t)^4}{12}\Bigg|_{-2t}^{\phantom{-2}t}=\dfrac{(3t)^4}{12}=\dfrac{27t^4}{4}\\
\end{align*}
$t < 0$ үед мөн адил $$S=-\int_{t}^{-2t}(x+2t)(x-t)^2\,dt=\dfrac{27t^4}{4}$$ байна.
