Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Талбайн нийлбэрийн хамгийн бага утга
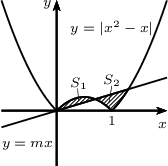
$y=|x^2-x|$ муруйг $y=mx$ шулуун 3 ялгаатай цэгээр огтолдог байв. Муруй ба шулууны огтлолд үүсэх 2 дүрсийн талбайн нийлбэр хамгийн бага байх $m$-ийг ол. Тэр үеийн талбайг ол.
Бодлогын төрөл: Уламжлалт
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар:
Бодолт: $C\colon y=|x^2-x|$, $\ell\colon y=mx$ гэе.
$C$ нь $y=\left\{
\begin{array}{rc} x^2-x, & x\le 0\lor x\ge1\\
x-x^2, & 0< x< 1
\end{array}\right.$ байна.
Хэрэв $|x^2-x|=mx$ тэгшитгэл $0< x< 1$ завсарт шийдтэй бол $C$ ба $\ell$ нь 3 цэгээр огтолцоно.
$-x^2+x=mx$ буюу $x=0$, $x=1-m$ болно. Иймд
$0< m< 1$ үед 3 ерөнхий цэгтэй.
$|x^2-x|=mx$ тэгшитгэл $0\leq x\leq 1$ үед $-x^2+x=mx \Rightarrow
x=1-m$, $x=0$ $0>x \cup 1< x$ үед $x^2-x=mx \Rightarrow x=1+m$ тул
\begin{align*} S_1&=\int\limits_{0}^{1-m}((-x^2+x)-mx)\,\textrm{d}x=-\int\limits_{0}^{1-m}x(x-(1-m))\,\textrm{d}x= \dfrac{(1-m)^3}{6}\\ S_2&=\int\limits_{1-m}^{1}(mx-(-x^2+x))\,\textrm{d}x+\int\limits_{1}^{1-m}(mx-(x^2-x))\,\textrm{d}x=\\ &=\bigg(\dfrac{x^3}{3}+(m-1)\cdot\dfrac{x^2}{2}\bigg)\Bigg|_{1-m}^{1}+\bigg(-\dfrac{x^3}{3}+(m+1)\cdot\dfrac{x^2}{2}\bigg)\Bigg|_{1}^{1+m}=m^2 \end{align*}
$S=S_1+S_2=\dfrac16(-m^3+9m^2-3m+1)$ болно. $S'=-\dfrac12(m^2-6m+1)$
$m^2-6m+1=0$, $0< m< 1$ учир $m=3-2\sqrt{2}$ болно. $S$ нь $m=3-2\sqrt{2}$ үед $\dfrac{23-16\sqrt{2}}{3}$ хамгийн бага утга авна.
\begin{align*} S_1&=\int\limits_{0}^{1-m}((-x^2+x)-mx)\,\textrm{d}x=-\int\limits_{0}^{1-m}x(x-(1-m))\,\textrm{d}x= \dfrac{(1-m)^3}{6}\\ S_2&=\int\limits_{1-m}^{1}(mx-(-x^2+x))\,\textrm{d}x+\int\limits_{1}^{1-m}(mx-(x^2-x))\,\textrm{d}x=\\ &=\bigg(\dfrac{x^3}{3}+(m-1)\cdot\dfrac{x^2}{2}\bigg)\Bigg|_{1-m}^{1}+\bigg(-\dfrac{x^3}{3}+(m+1)\cdot\dfrac{x^2}{2}\bigg)\Bigg|_{1}^{1+m}=m^2 \end{align*}
$S=S_1+S_2=\dfrac16(-m^3+9m^2-3m+1)$ болно. $S'=-\dfrac12(m^2-6m+1)$
| $m$ | $0$ | $\boldsymbol{\cdots}$ | $3-2\sqrt{2}$ | $\boldsymbol{\cdots}$ | $1$ |
| $S'$ | $-$ | $0$ | $+$ | ||
| $S$ | $y$ | $\min$ | $\nearrow$ |
$m^2-6m+1=0$, $0< m< 1$ учир $m=3-2\sqrt{2}$ болно. $S$ нь $m=3-2\sqrt{2}$ үед $\dfrac{23-16\sqrt{2}}{3}$ хамгийн бага утга авна.
Сорилго
Энэ бодлого ямар нэг сорилгод ороогүй.