Монгол Бодлогын Сан

Заавар: $S_1=S_2 \Rightarrow \mathop{\int\limits_{a}^{b}}(f(x)-g(x))\,\textrm{d}x=\mathop{\int\limits_{b}^{c}}(g(x)-f(x))\,\textrm{d}x$ буюу $\mathop{\int\limits_{a}^{b}}(f(x)-g(x))\,\textrm{d}x+\mathop{\int\limits_{b}^{c}}(f(x)-g(x))\,\textrm{d}x= \mathop{\int\limits_{a}^{c}}(f(x)-g(x))\,\textrm{d}x=0$

Бодолт: $C$ ба $\ell$ нь 3 ерөнхий цэгтэй байхын тулд $m$ нь $C$ муруйн $x=0$ цэг дээрх шүргэгч шулууны өнцгийн коэффициентээс бага байх ёстой. Иймд $0< m< 9$ нөхцөл хангана. $x(x-3)^2=mx\Rightarrow x=0, x=3-\sqrt{m}, x=3+\sqrt{m}$ байна. 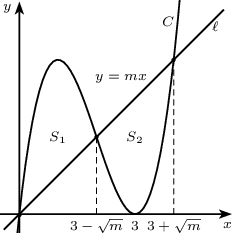2 хэсэг талбай тэнцүү байх нөхцөл нь $$\int\limits_{0}^{3-\sqrt{m}}\kern-5pt\{(x^3-6x^2+9x)-mx\}\,\textrm{d}x=\kern-5pt\int\limits_{3-\sqrt{m}}^{3+\sqrt{m}}\kern-5pt\{mx-(x^3-6x^2+9x)\}\,\textrm{d}x$$ юм. Эндээс $$\int\limits_{0}^{3+\sqrt{m}}\{(x^3-6x^2+9x)-mx\}\,\textrm{d}x=0$$ буюу $$\bigg[\dfrac{x^4}{4}-2x^3+\dfrac{9x^2}{2}-\dfrac{mx^2}{2}\bigg]\Bigg|_{0}^{3+\sqrt{m}}\kern-5pt=0\Leftrightarrow$$ $$(3+\sqrt{m})^2\bigg[\dfrac{(3+\sqrt{m})^2}{4}-2(3+\sqrt{m})+\dfrac{9}{2}-\dfrac{m}{2}\Bigg]=0$$ болно. $3+\sqrt{m}>0$ тул $$-m-2\sqrt{m}+3=0\Leftrightarrow(\sqrt{m}-1)(\sqrt{m}+3)=0$$ $0< m< 9$ тул $m=1$ байна.