Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
ЭЕШ 2015 D №29
$AB$, $CD$ суурьтай $ABCD$ трапецын диагоналиудын огтлолцлын цэг $O$ байг. $BO=4$, $OD=8$ ба $AB=10$ бол трапецын дундаж шугамын уртыг ол.
A.$7.5$ B.$20$ C.$30$ D.$15$ E.$25$
Бодлогын төрөл:Сонгох
Амжилтын хувь:36.82%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар: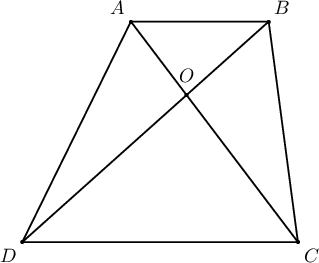
$\triangle AOB\sim\triangle COD$-д төсөөгийн харьцаа бич.
Бодолт:$\triangle AOB\sim\triangle COD$ тул
$$\dfrac{AB}{CD}=\dfrac{BO}{OD}=\dfrac{4}{8}\Rightarrow CD=2AB=20$$
Иймд дундаж шугамын урт нь $\dfrac{AB+CD}{2}=\dfrac{10+20}{2}=15$.