Монгол Бодлогын Сан

Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.

$y=\dfrac{x-2}{x-1}$ функц өгөгдөв.

$y=\dfrac{x-2}{x-1}$ функцийн $x_0=2$ цэгт татсан шүргэгч шулууны тэгшитгэлийг бичвэл $y=\fbox{a}x-\fbox{b}$ ;
$y=\dfrac{x-2}{x-1}$ , $x=2$ , $x=5$ ба $y=0$ шугамуудаар хүрээлэгдсэн дүрсийн талбай $\fbox{c}-\ln\fbox{d}$ ;
$y=5x+5$ шулуунд перпендикулар ба $(1;1)$ цэгийг дайрсан шулууны тэгшитгэл нь $\fbox{e}x+\fbox{f}y-6=0$ ;
$y=\dfrac{x-2}{x-1}$ муруй ба $x-3y-2=0$ шулууны огтлолцлын цэгүүдийн хоорондох зай $\dfrac{2}{3}\sqrt{\fbox{gh}}$ .

ab = 12

cd = 34

ef = 15

gh = 10

Бодлогын төрөл: Нөхөх

Амжилтын хувь: 24.25%

Заавар:

$y=f(x)$ функцийн графикийн $(x_0,f(x_0))$ цэгт татсан шүргэгч шулууны тэгшитгэл: $y=f^\prime(x_0)(x-x_0)+f(x_0)$
$[a,b]$ мужийн дурын $x$ цэг дээр $g(x)\le f(x)$ бол $x=a$ , $x=b$ , $y=f(x)$ , $y=g(x)$ муруйнуудаар үүсэх дүрсийн талбай нь $S=\int_a^b [f(x)-g(x)]\,\mathrm{d}x$ байна.
Харилцан перпендикуляр шулуунуудын өнцгийн коэффициентүүдийн үржвэр $-1$ байдаг.
$y=f(x)$ , $y=g(x)$ муруйнуудын огтолцлын цэгийн координат нь $\bigg\{\begin{array}{c} y=f(x)\\ y=g(x)\end{array}$ систем тэгшитгэлийн шийд байна. Иймд $f(x)=g(x)$ тэгшитгэлийг бодож огтолцлын цэгийн ординатуудыг олно.

Бодолт: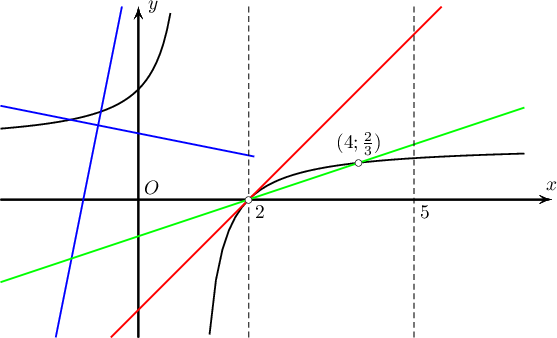

$y^\prime=\dfrac{(x-2)^\prime(x-1)-(x-1)^\prime(x-2)}{(x-1)^2}=\dfrac{1}{(x-1)^2}$ . $y-y_0=y_0^\prime(x-x_0)\Rightarrow y-\dfrac{2-2}{2-1}=\dfrac{1}{(2-x)^2}(x-2)\Rightarrow y=x-2$
$\displaystyle\int_{2}^5\Big|\dfrac{x-2}{x-1}-0\Big|\,\,\mathrm{d}x=\int_2^5\Big(1-\dfrac{1}{x-1}\Big)\,\,\mathrm{d}x=(x-\ln(x-1))\Big|_2^5=3-\ln 4$
Перпендикуляр шулуунуудын өнцгийн коэффициентүүдийн үржвэр $-1$ тул $y=–\dfrac15x+b$ ба $1=-\dfrac15\cdot1+b\Rightarrow b=\dfrac{6}{5}$ тул $y=-\dfrac15x+\dfrac65\Rightarrow x+5y-6=0$ байна.
Оглолцлын цэгийн координат нь $\left\{\begin{array}{c} y=\dfrac{x-2}{x-1}\\ x-3y-2=0 \end{array}\right.$ системийн шийд байна. Орлуулга хийж бодвол $y=\dfrac{3y}{3y+1}\Rightarrow y_1=0, y_2=\dfrac{2}{3}\Rightarrow x_1=2, x_2=4$ тул $(2;0)$ , $\big(4;\frac23\big)$ цэгүүдийн хоорондох зай нь $d=\sqrt{(4-2)^2+\left(\frac23-0\right)^2}=\sqrt{\dfrac{4\cdot 9+4}{9}}=\dfrac23\sqrt{10}$