Монгол Бодлогын Сан

Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.

$U=\{1,2,3,4,5,6,7,8,9\}$ -ийн $A=\{1,2,4,6,8\}$ , $B=\{1,3,6,9\}$ дэд олонлогийн хувьд дараах олонлогуудийг ол.

Бодлогын төрөл: Уламжлалт

Заавар:

$A\setminus B$ -ээр $A$ олонлогийн $B$ олонлогийн элемент болдоггүй бүх элементүүдээс тогтох дэд олонлогийг тэмдэглэдэг.
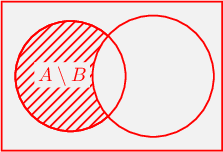
Ямар нэг $U$ (универсал) олонлогийн $A$ дэд олонлогийн элемент болдоггүй бүх элементүүдээс тогтох олонлог буюу $U\setminus A$ -г $A$ олонлогийн $U$ дахь гүйцээлт гэх ба $U$ олонлог нь ямар олонлог гэдэг нь тодорхой үед товчоор $\overline{A}$ гэж тэмдэглэнэ. $\forall x\in U\colon x\in \overline{A}\Leftrightarrow x\not\in A$
$A$ ба $B$ олонлогуудын ерөнхий элементүүдээс тогтох олонлогийг $A$ , $B$ олонлогуудын огтлолцол гээд $A\cap B$ гэж тэмдэглэнэ. $x\in A\cap B\Leftrightarrow x\in A\land x\in B$ Энд $\land$ нь логикийн ба холбоос (конъюнкц) юм.
$A$ ба $B$ олонлогуудын ядаж нэгд нь ордог элементүүдээс тогтох олонлогийг $A$ , $B$ олонлогуудын нэгдэл гээд $A\cup B$ гэж тэмдэглэнэ. $x\in A\cup B\Leftrightarrow x\in A\lor x\in B$ Энд $\lor$ нь логикийн эсвэл холбоос (дизъюнкц) юм.

Бодолт: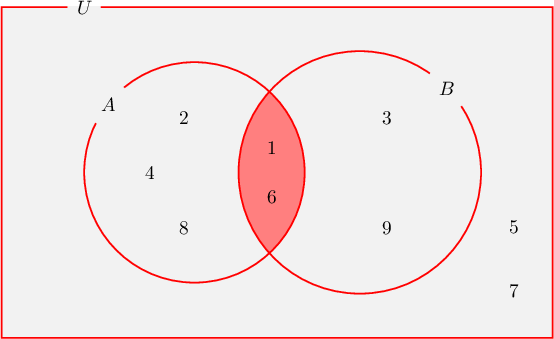

$A$ олонлогт харъяалагддаггүй $U$ -ийн элементүүд нь $3, 5, 7, 9$ тул $\overline{A}=\{3,5,7,9\}$ .
$\{3,5,7,9\}$ ба $\{1,3,6,9\}$ -ийн ерөнхий элемент нь $3, 9$ тул $\overline{A}\cap B=\{3,9\}$ .
$\overline{B}=\{2,4,5,7,8\}$ тул $\overline{A}\cap\overline{B}=\{5,7\}$ байна.
$\overline{A}$ ба $\overline{B}$ -ийн ядаж нэгд нь харъяалагддаг элементүүдийн олонлог нь $\overline{A}\cup\overline{B}=\{2,3,4,5,7,8,9\}$ .
$A\cap B=\{1,6\}$ тул $\overline{A\cap B}=\{2,3,4,5,7,8,9\}$ байна.
$A\cup B=\{1,2,3,4,6,8,9\}$ тул $\overline{A\cup B}=\{5,7\}$ байна.