Монгол Бодлогын Сан

Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.

Тойргийн $AB$ ба $AC$ хоёр хөвч ижил урттай ба хоорондох өнцөг нь $\dfrac{\pi}{3}$ хэмжээтэй юм.

Тойргийн төв $O$ гэвэл $\measuredangle BOC=\dfrac{2\pi}{\fbox{a}}$ ба $\measuredangle BOA=\dfrac{\fbox{b}\pi}{\fbox{c}}$ байна.
$AB$ ба $AC$ шулууны хооронд хашигдсан дугуйн хэсгийг дугуйн нийт талбайд харьцуулсан харьцаа $\dfrac{\fbox{d}\pi+3\sqrt{3}}{\fbox{e}\pi}$
$AB$ талын уртыг тойргийн радиуст харьцуулсан харьцаа $\sqrt{\fbox{f}}$ байна.

abc = 323

de = 26

f = 3

Бодлогын төрөл: Нөхөх

Амжилтын хувь: 19.33%

Заавар:

Тойргийн нумд тулсан өнцөг нь төв өнцгийнхөө хагастай тэнцүү байдаг.
Энэ дүрсийн талбай нь $BOC$ сектор, $AOB$, $AOC$ гурвалжнуудын талбайн нийлбэртэй тэнцүү байна.
$ABC$ гурвалжны талбай $S=\dfrac12 AB^2\sin60^\circ=3 S_{AOB}$ байна.

Бодолт: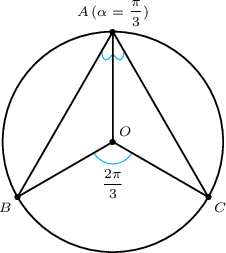

Тойргийн нумд тулсан өнцөг нь төв өнцгийнхөө хагастай тэнцүү байдаг. Иймд $$\measuredangle BAC=\dfrac{\measuredangle BOC}{2}\Rightarrow \measuredangle BOC=2\cdot\measuredangle BAC=\dfrac{2\pi}{3}$$ Нөгөө талаас $ABC$ нь зөв гурвалжин тул $$\measuredangle BOA=\measuredangle BOC=\dfrac{2\pi}{3}$$
Дугуйн талбай нь $S=\pi R^2$. $BOC$ секторын төв өнцөг $\dfrac{2\pi}{3}$ нь $2\pi$-ийн $\dfrac13$ тул талбай нь $\dfrac{S}{3}=\dfrac{\pi R^2}{3}$ байна. $$S_{\triangle AOB}=S_{\triangle AOC}=\dfrac12R^2\sin\dfrac{2\pi}{3}=\dfrac{R^2\sqrt{3}}{4}$$ тул $AB$ ба $AC$-ийн хооронд хашигдсан дүрсийн талбай нь $$2\cdot\dfrac{R^2\sqrt{3}}{4}+\dfrac{\pi R^2}{3}=\dfrac{R^2\sqrt{3}}{2}+\dfrac{\pi R^2}{3}$$ болох ба бидний олох харьцаа нь $$\dfrac{\dfrac{R^2\sqrt{3}}{2}+\dfrac{\pi R^2}{3}}{\pi R^2}=\dfrac{2\pi+3\sqrt3}{6\pi}.$$
$S=\dfrac12 AB^2\sin60^\circ=3 S_{AOB}=\dfrac{3\sqrt3 R^2}{4}\Rightarrow AB^2=3R^2\Rightarrow f=3$ байна.