Монгол Бодлогын Сан

Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.

$f(x)=3x^3-6x^2+3x+5$ функц нь

$\bigg]-\infty;\dfrac{\fbox{a}}{\fbox{b}}\bigg[\cup]\fbox{c};+\infty[$ завсарт өсөж, $\bigg]\dfrac{\fbox{a}}{\fbox{b}};\fbox{c}\bigg[$ завсарт буурна.
$[0;3]$ завсар дээрх хамгийн бага утга нь $y_{\min}=\fbox{d}$ , хамгийн их утга нь $y_{\max}=\fbox{ed}$ .
$3x^3-6x^2+3x+5=0$ тэгшитгэл нь $\fbox{g}$ ширхэг бодит шийдтэй.

abc = 131

def = 541

g = 1

Бодлогын төрөл: Нөхөх

Амжилтын хувь: 24.30%

Заавар:

Функцийн өсөх муж нь түүний уламжлал нь эерэг байх муж, буурах муж нь түүний уламжлал нь сөрөг байх муж байна.
Функцийн $[a;b]$ завсар дахь ХИ (хамгийн их), ХБ (хамгийн бага) утгууд нь эсвэл мужийн хил буюу $x=a$ , $x=b$ цэгүүд дээрх утгууд, эсвэл түүний сэжигтэй цэгүүд буюу тухайн муж дахь уламжлал нь 0-тэй тэнцэх аргумент дээрх утгууд байна. Өөрөөр хэлбэл дээр дурьдсан цэгүүд дээрх утгуудын хамгийн их нь ХИУ, хамгийн бага нь ХБУ болно.
$f(x)=0$ куб тэгшитгэл нь 1-ээс 3 бодит шийдтэй байх боломжтой.

Энд функц гэдгийн дор дифференциалчлагдах функцийг ойлгоорой!

Бодолт:

$(a(x)\pm b(x))^\prime=a^\prime(x)\pm b^\prime(x)$ ба $(ax^{\color{red}{n}})=a\cdot {\color{red}{n}}\cdot x^{{\color{red}{n-1}}}$ тул $f^\prime(x)=(3x^3-6x^2+3x+5)^\prime=(3x^3)^\prime-(6x^2)^\prime+(3x)^\prime+5^\prime=$ $=3\cdot {\color{red}{3}}\cdot x^{{\color{red}{3-1}}}-6\cdot {\color{red}{2}}\cdot x^{{\color{red}{2-1}}}+3\cdot {\color{red}{1}}\cdot x^{{\color{red}{1-1}}}+0=9x^2-12x+3$ байна. $f^\prime(x)>0\Leftrightarrow 9x^2-12x+3=9(x-\tfrac13)(x-1)>0\Leftrightarrow x\in]-\infty;\tfrac13[\cup]1;+\infty[$ мужид өсөх ба $f^\prime(x)<0\Leftrightarrow x\in]\tfrac13;1[$ мужид буурна.
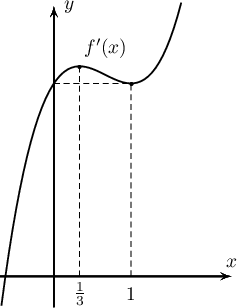
Функцийн $x=0$ , $x=\frac13$ , $x=1$ , $x=3$ дахь утгуудыг бодъё: $\begin{align*} f(0)&=3\cdot 0^3-6\cdot 0^2+3\cdot 0+5=5\\ f\bigg(\frac13\bigg)&=3\cdot \bigg(\frac13\bigg)^3-6\cdot \bigg(\frac13\bigg)^2+3\cdot \bigg(\frac13\bigg)+5=5\frac49\\ f(1)&=3\cdot 1^3-6\cdot 1^2+3\cdot 1+5=5\\ f(3)&=3\cdot 3^3-6\cdot 3^2+3\cdot 3+5=41\\ \end{align*}$ Иймд $\text{ХБУ}=5$ , $\text{ХИУ}=41$
Функцийн графикаас харахад $x\ge 0$ үед $f(x)\ge 5$ тул $f(x)=0$ тэгшитгэл шийдгүй. $x<0$ үед $f(x)$ өсдөг функц тул $OX$ тэнхлэгийг цор ганц цэгээр огтлох боломжтой. Иймд $f(x)=0$ тэгшитгэл цор ганц шийдтэй байна.