Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Тойрогт багтсан квадрат
Квадратын талбайг уг квадратыг багтаасан дугуйн талбайд харьцуулсан харьцаа аль нь вэ?
A.$\dfrac{1}{\pi}$ B.$\dfrac{\pi}{2}$ C.$\dfrac{2}{\pi}$ D.$\dfrac{4}{\pi}$ E.$\dfrac{\pi}{4}$
Бодлогын төрөл:Сонгох
Амжилтын хувь:39.38%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:Багтсан квадратын диагональ нь $2R$ тул $a=2R\cos 45^\circ$ байна.
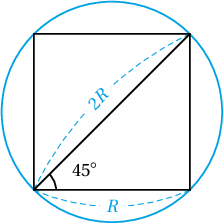
Бодолт:Квадратын талбай нь $$S=a^2=(2R\cos45^\circ)^2=\big(2R\tfrac{\sqrt2}{2}\big)^2=2R^2.$$
Дугуйн талбай $\pi R^2$ тул харьцаа нь $\dfrac{2R^2}{\pi R^2}=\dfrac{2}{\pi}$.
Сорилго
2017-06-07 2016-06-04 Геометр сэдвийн давтлага 1 Сорилго 3 2020-03-09 сорил Тойрог, түүнтэй холбоотой бодлогууд СЕКТОР СЕГМЕНТИЙН ТАЛБАЙ Геометр сэдвийн давтлага 1 тестийн хуулбар Circle Тойргийн нумын урт, дугуйн секторын талбай Нумын урт, Сектор