Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
ЭЕШ 2011 D №17
$ABC$ гурвалжны хувьд $AC=8$, $\angle ACB=105^\circ$, $\angle ABC=30^\circ$ ба орто төв $H$ бол $AH$ хэрчмийн уртыг ол.
A. $2\sqrt6$
B. $2\sqrt2$
C. $8\sqrt2$
D. $8$
E. $\dfrac{8\sqrt6}{3}$
Бодлогын төрөл: Сонгох
Амжилтын хувь: 32.61%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $\cos\measuredangle CAC_1$, $\cos\measuredangle HAC_1$ өнцгүүдийн косинусыг $\measuredangle AC_1H=90^\circ$ болохыг ашиглан ол.
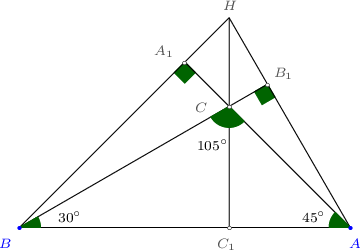
Бодолт: $\triangle BB_1A$ тэгш өнцөгт гурвалжнаас $\measuredangle B_1AB=\measuredangle C_1AH=90^\circ-30^\circ=60^\circ$ байна.
$\triangle ACC_1$ тэгш өнцөгт гурвалжнаас $\cos CAC_1=\dfrac{AC_1}{AC}\Rightarrow AC_1= AC\cdot\cos 45^\circ=8\cdot \dfrac{\sqrt2}{2}=4\sqrt2$.
$\triangle HAC_1$ тэгш өнцөгт гурвалжнаас $\cos\measuredangle C_1AH=\dfrac{AC_1}{AH}\Rightarrow AH=\dfrac{4\sqrt3}{\cos 60^\circ}=8\sqrt2$ байна.
$\triangle ACC_1$ тэгш өнцөгт гурвалжнаас $\cos CAC_1=\dfrac{AC_1}{AC}\Rightarrow AC_1= AC\cdot\cos 45^\circ=8\cdot \dfrac{\sqrt2}{2}=4\sqrt2$.
$\triangle HAC_1$ тэгш өнцөгт гурвалжнаас $\cos\measuredangle C_1AH=\dfrac{AC_1}{AH}\Rightarrow AH=\dfrac{4\sqrt3}{\cos 60^\circ}=8\sqrt2$ байна.