Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
ЭЕШ 2015 A №37
$AB$, $CD$ суурьтай $ABCD$ трапецийн талууд $AB=30$, $BC=20$, $CD=5$ ба $DA=15$ байг.
- Трапецийн дундаж шугамын урт $\dfrac{\fbox{ab}}{2}$
- Трапецийн өндөр $\fbox{cd}$
- Трапецийн талбай $\fbox{efg}$
ab = 35
cd = 12
efg = 210
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 33.16%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: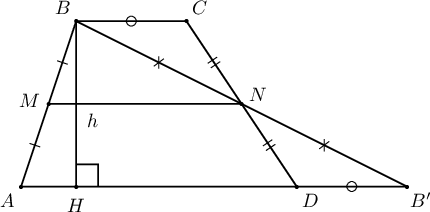 
Трапецийн дундаж шугамын урт нь сууриудын арифметик дундаж:
$$MN=\dfrac{AB'}{2}=\dfrac{AD+BC}{2}$$
талбай нь өндрийг дундаж шугамын уртаар үржүүлэхэд гарна:
$$S_{ABCD}=S_{\triangle ABB'}=\dfrac{1}{2}AB'\cdot h=MN\cdot h$$
Бодолт:
- Дундаж шугамын урт нь $\dfrac{30+5}{2}=\dfrac{35}{2}$;
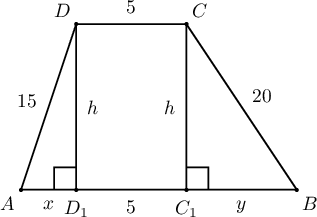
- $C$, $D$ оройгоос буусан өндрийн сууриуд нь харгалзан $C_1$, $D_1$ ба $AD_1=x$, $BC_1=y$ өндрийг $h$ гэвэл Пифагорын теорем ёсоор
$$15^2-h^2=x^2,$$
$$20^2-h^2=y^2$$
ба $x+y=30-5=25$ байна. Эндээс $$20^2-15^2=y^2-x^2=(y-x)(y+x)=25(y-x)\Rightarrow y-x=7$$ тул $x=9$, $y=16$ б $h=\sqrt{15^2-9^2}=\sqrt{144}=12$.
- Трапецийн талбай нь $\dfrac{35}{2}\cdot 12=210$.
Сорилго
ЭЕШ 2015 A
2016-04-25
hw-56-2016-06-15
ЭЕШ 2015 A alias
сорил-5
ЭЕШ 2015 A тестийн хуулбар
Даалгавар 3