Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
ЭЕШ 2007 A №27
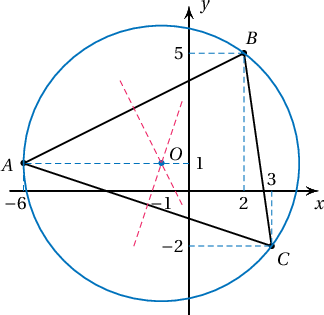
$A(-6;1)$, $B(2;5)$, $C(3;-2)$ цэгүүдэд оройтой гурвалжин байв.
- $C$ оройн медианы тэгшитгэл $y=-\fbox{a}x+1$ бол $a$-г ол.
- $\overrightarrow{AC}$, $\overrightarrow{AB}$ векторын хоорондох өнцөг болох $A$ оройн дотоод өнцгийг $\alpha$ гэвэл $\alpha=\fbox{bc}^\circ$ байна.
- Гурвалжныг багтаасан тойргийн тэгшитгэл нь $$(x+\fbox{d})^2+(y-\fbox{e})^2=\fbox{f}^2$$
a = 1
bc = 45
def = 115
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 25.32%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар:
- $A(x_1,y_1)$, $B(x_2,y_2)$ бол $AB$ хэрчмийн дундаж цэгийн координат нь $$\left(\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2}\right)$$ байх ба $AB$ шулууны тэгшитгэл $$\dfrac{x-x_1}{x_2-x_1}=\dfrac{y-y_1}{y_2-y_1}$$
- $\vec{m}=(x_1,y_1)$, $\vec{n}=(x_2,y_2)$ векторуудын хоорондох өнцгийн косинус нь $$\cos\alpha=\dfrac{\vec{m}\cdot\vec{n}}{|\vec{m}|\cdot|\vec{n}|}=\dfrac{x_1x_2+y_1y_2}{\sqrt{x_1^2+y_1^2}\cdot\sqrt{x_2^2+y_2^2}}$$
- Талуудын дундаж перпендикуляр шулуунуудын тэгшитгэлийг бичиж огтлолцолын цэгийг ол. Энэ нь багтаасан тойргийн төв юм. Үүнийг зургаас илүү хялбархан олж болохыг санаарай.
Бодолт:
- $AB$ хэрчмийн дундаж цэгийн координат нь $$M\left(\dfrac{-6+2}{2},\dfrac{1+5}{2}\right)=M(-2,3)$$ байх ба $CM$ шулууны тэгшитгэл $$\dfrac{x-3}{-2-3}=\dfrac{y-(-2)}{3-(-2)}\Leftrightarrow -x+3=y+2$$ тул $$y=-x+1$$
- $\overrightarrow{AB}=B-A=(2;5)-(-6;1)=(8;4)$, $\overrightarrow{AC}=(3;-2)-(-6;1)=(9;-3)$ векторуудын хоорондох өнцгийн косинус нь $$\cos\alpha=\dfrac{8\cdot 9+4\cdot(-3)}{\sqrt{\mathstrut 8^2+4^2}\cdot\sqrt{9^2+(-3)^2}}=\dfrac{60}{4\sqrt{5}\cdot 3\sqrt{10}}=\dfrac{\sqrt2}{2}$$ тул $\alpha=45^\circ$ болно.
- $AB$ хэрчмийн дундаж цэг нь $\dfrac{A+B}{2}=\dfrac{(-6,1)+(2,5)}{2}=(-2,3)$, $\overrightarrow{AB}=(2-(-6),5-1)=(8,4)$ тул дундаж перпендикуляр шулууны тэгшитгэл нь
$$8(x-(-2))+4(y-3)=0\Leftrightarrow y=-2x-1$$
$AC$ хэрчмийн дундаж цэг нь $\dfrac{A+C}{2}=\dfrac{(-6,1)+(3,-2)}{2}=(-1.5,-0.5)$, $\overrightarrow{AC}=(3-(-6),-2-1)=(9,-3)$ тул дундаж перпендикуляр улууны тэгшитгэл нь
$$9(x-(-1.5))-3(y-(-0.5))=0\Leftrightarrow y=3x+4$$
болно. Иймд багтаасан тойргийн төв нь
$$\left\{\begin{array}{c}
y=-2x-1\\
y=3x+4
\end{array}\right.\Rightarrow -2x-1=3x+4\Rightarrow x=-1, y=1$$
координаттай байна. (Зургаа зөв зураад зургаасаа багтаасан тойргийн төвийг олбол илүү хурдан байх боломжтой.)
Багтаасан тойргийн радиус нь $R=OA=|(-1)-(6)|=5$ болно. Иймд тэгшитгэл нь $$(x+1)^2+(y-1)^2=5^2$$ байна.
Сорилго
ЭЕШ 2007 A
2017-09-10
2017-03-17
Огторгуйн геометр 2
2020-05-05 сорил
2020-06-10 сорил
Синусын теорем
Синус, косинусын теорем
Огторгуйн геометр 2 тестийн хуулбар
ЭЕШ 2007 A тест
Математик ЭЕШ