Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
ЭЕШ 2007 A №28
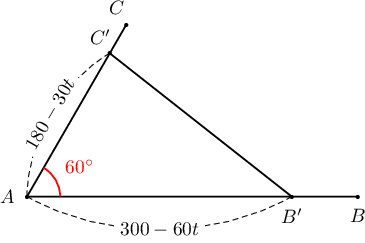
$A$ цэгээс салаалсан, хоорондоо $60^\circ$ өнцөг үүсгэх хоёр шулуун замын нэгэн дээр уулзвараас 300км зайд байгаа $B$ цэгээс 60км/ц хурдтай машин, нөгөө дээр нь уулзвараас 180км зайд байгаа $C$ цэгээс 30км/ц хурдтай машин нэгэн зэрэг уулзварын зүг хөдөлжээ.
- Тэдгээрийн хоорондох зай $\fbox{a}$ цагийн дараа хамгийн бага болно. $\text{a}$ хэд вэ?
- Энэ зай нь $\fbox{bc}$км байна. $\text{b, c}$-г ол.
a = 5
bc = 30
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 32.37%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $t$ хугацааны дараах хоёр цэгийн хоорондох зайг $S(t)$ гэвэл косинусын теорем ёсоор
$$[S(t)]^2=(300-60t)^2+(180-30t)^2-2(300-60t)(180-30t)\cos60^\circ$$
байна.

Бодолт: Хоёр цэгийн хоорондох зай нь ямагт эерэг тоо байх тул $S(t)$ ба $[S(t)]^2$-үүд нэг ижил хугацаанд хамгийн бага утгаа авна. Иймд $[S(t)]^2$ хамгийн бага байх $t$-ийн утгыг олъё.
\begin{align*}
[S(t)]^2&=(300-60t)^2+(180-30t)^2-2(300-60t)(180-30t)\cos60^\circ\\
&=60^2(25-10t+t^2)+30^2(36-12t+t^2)-2\cdot 60\cdot 30\cdot(5-t)(6-t)\cdot\dfrac12\\
&=900\cdot \{100-40t+4t^2+36-12t+t^2-2(t^2-11t+30)\}\\
&=900\cdot(3t^2-30t+76)=900\cdot\{3(t-5)^2+1\}
\end{align*}
тул $t=5$ үед хамгийн бага утга авна. Энэ үед $S(t)=\sqrt{900}=30$ байна.
Сорилго
ЭЕШ 2007 A
2017-09-18
uguulbertei
2016-12-07
ЭЕШ өгүүлбэртэй бодлогууд
Косинусын теорем
Косинусын теорем тестийн хуулбар
ЭЕШ 2007 A тест