Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
ЭЕШ 2007 A №30
Хавтгай дээр хоорондоо 6 нэгж зайтай $A$ цэг ба $m$ шулуун байв.
- Энэ цэг ба шулуунаас ижил зайд байрлах цэгүүдийн олонлог нь $y=\dfrac{x^2}{\fbox{ab}}$ функцийн график болох муруйг дүрсэлнэ. $\text{a}$ ба $\text{b}$ нь хэд вэ?
- Энэ муруйн тэгш хэмийн тэнхлэгээс хоёр тийш 18 нэгж зайд түүнтэй параллель байрлах $m_1$ ба $m_2$ шулуун болон $y=\dfrac{x^2}{\fbox{ab}}$ муруй, $m$ шулууны хооронд хашигдсан дүрсийн талбай нь $S=\fbox{cde}$ байна.
ab = 12
cde = 432
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 8.48%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $A(0;3)$, $m\colon x=-3$ гээд бод. (Ер нь бодлогын нөхцлийг хангах цэг ба шулуун төгсгөлгүй олон олдох бөгөөд тухай бүрт нь тэгшитгэл нь өөр өөр гарах тул энэ бодлогын нөхцөл дутуу юм). Дүрсийн талбай нь $$\int\limits_{-18}^{18}\bigg(\frac{x^2}{12}+3\bigg) \,\mathrm{d}x$$
байна.
Бодолт:
- $A(0,3)$ ба $B(x,y)$ нь $A$ цэг ба $m\colon x=-3$ шулуунаас ижил зайд алслагдсан цэг гэвэл $$AB^2=x^2+(y-3)^2$$ байна. Харин $B$ цэгээс $m$ шулуун хүртэлх зай нь $$d(B,m)=|y-(-3)|=|y+3|$$ байна. $AB=d(B,m)$ тул
$$x^2+(y-3)^2=(y+3)^2\Rightarrow y=\dfrac{1}{12}x^2$$
болно.
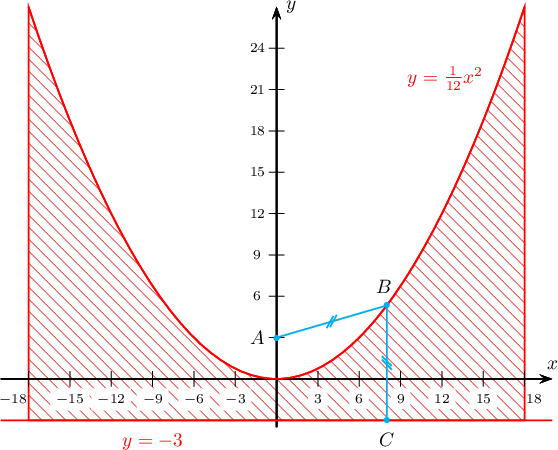
- Олох дүрсийн талбай нь $$\int\limits_{-18}^{18}\bigg(\frac{x^2}{12}+3\bigg) \,\mathrm{d}x=\bigg(\frac{x^3}{36}+3x\bigg)\Bigg|_{-18}^{18}=2\bigg(\frac{18^3}{36}+3\cdot18\bigg)=432$$