Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Параметрээс хамаарсан илэрхийллийн ХБУ
$x^2+(a+1)x+2a=0$ тэгшитгэл $x_1$, $x_2$ гэсэн 2 бодит шийдтэй (ялгаатай байх албагүй) байв. $x_1^2+x_2^2$-ийн утга хамгийн бага байх $a$ параметрийн утгыг ол.
A.$a=1$ B.$a=3-2\sqrt2$ C.$a=3+2\sqrt2$ D.$a=-1$ E.$a=0$
Бодлогын төрөл:Сонгох
Амжилтын хувь:37.50%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:$$D=(a+1)^2-8a\ge 0\Leftrightarrow a^2-6a+1\ge 0\Leftrightarrow$$
$$a\le 3-2\sqrt2\cup a\ge 3+2\sqrt2$$
болохыг анхаар!
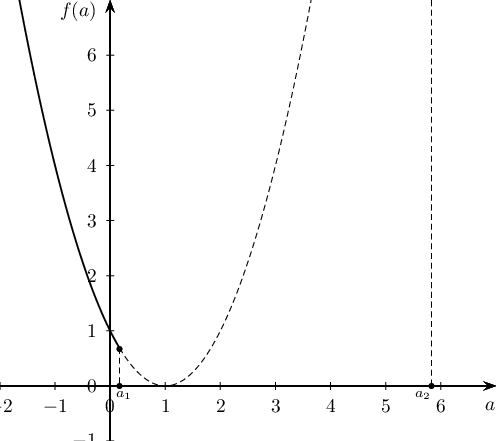
Бодолт:$x_1^2+(a+1)x_1+2a=0$, $x_2^2+(a+1)x_2+2a=0$ ба Виетийн теорем ёсоор $x_1+x_2=-(a+1)$ тул $$f(a)=x_1^2+x_2^2=-(a+1)(x_1+x_2)-4a=(a+1)^2-4a=(a-1)^2$$
болно. Энэ илэрхийлэл нь $a\le a_1=3-2\sqrt2\cup a\ge a_2=3+2\sqrt2$ мужид хамгийн бага утгаа $a_1=3-2\sqrt2$ цэг дээр авна.
Сорилго
2017-08-25 Бие даалт 7 Алгебрийн тэгшитгэл - Квадрат тэгшитгэл алгебр алгебр Квадрат Тэгшитгэл, Тэнцэтгэл биш 2022-2023 хичээлийн жил