Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Катетуудыг шүргэсэн тойрог
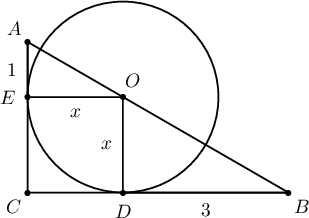
$ABC$ тэгш өнцөгт гурвалжны $AB$ гипотенуз дээр төв нь орших тойрог $AC$ ба $BC$ талуудыг харгалзан $E$, $D$ цэгүүдээр шүргэв. Хэрэв $AE=1$, $BD=3$ бол $\measuredangle BAC=\fbox{ab}^\circ$, $\triangle ABC$-ийн периметр нь $\fbox{c}+\fbox{d}\sqrt3$, багтсан тойргийн радиус $\fbox{e}$ байна.
ab = 60
cd = 64
e = 1
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 41.43%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $\triangle AOE\sim\triangle OBD$ болохыг ашиглаарай!
Багтсан тойргийн радиусыг $r=\dfrac{a+b-c}{2}$, $r=\dfrac{S}{p}$-ийн аль нэгээр олж болно. Энд $a$, $b$ нь тэгш өнцөгт гурвалжны катетуудын урт, $c$ нь гипотенуз, $p$ нь хагас периметр.
Багтсан тойргийн радиусыг $r=\dfrac{a+b-c}{2}$, $r=\dfrac{S}{p}$-ийн аль нэгээр олж болно. Энд $a$, $b$ нь тэгш өнцөгт гурвалжны катетуудын урт, $c$ нь гипотенуз, $p$ нь хагас периметр.
Бодолт: $\triangle AOE\sim\triangle OBD$ тул
$$\tg\measuredangle BAC=\dfrac{OE}{AE}=\dfrac{BD}{OD}$$
байна. $OE=OD=x$ тул $x^2=3\Rightarrow x=\sqrt3$ байна.
Иймд $\tg\measuredangle BAC=\sqrt3\Rightarrow\measuredangle BAC=60^\circ$ ба $AC=1+\sqrt3$, $BC=3+\sqrt3$ байна.
Пифагорын теоремоор $AB^2=AC^2+BC^2$ тул $$AB^2=(1+\sqrt3)^2+(3+\sqrt3)^2=16+8\sqrt3=(2+2\sqrt3)^2$$ буюу $AB=2+2\sqrt3$ болно. Иимд $ABC$ гурвалжны периметр нь $$2+2\sqrt3+1+\sqrt3+3+\sqrt3=6+4\sqrt3$$
Багтсан тойргийн радиус нь $$r=\dfrac{1+\sqrt3+3+\sqrt3-2-2\sqrt3}{2}=1$$ байна.
Пифагорын теоремоор $AB^2=AC^2+BC^2$ тул $$AB^2=(1+\sqrt3)^2+(3+\sqrt3)^2=16+8\sqrt3=(2+2\sqrt3)^2$$ буюу $AB=2+2\sqrt3$ болно. Иимд $ABC$ гурвалжны периметр нь $$2+2\sqrt3+1+\sqrt3+3+\sqrt3=6+4\sqrt3$$
Багтсан тойргийн радиус нь $$r=\dfrac{1+\sqrt3+3+\sqrt3-2-2\sqrt3}{2}=1$$ байна.