Монгол Бодлогын Сан

Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.

$f(x)=\cos4x+\cos(2x-\pi)$ функцийн хувьд

Үндсэн үе $T=\fbox{a}\pi$;
Хамгийн их утга: $\fbox{b}$;
Хамгийн бага утга: $-\dfrac{\fbox{c}}{\fbox{d}}$;
$f(x)=0$ тэгшитгэлийн шийд $x=\fbox{e}\pi$, $x=\pm\dfrac{\pi}{\fbox{f}}+\pi k$, $k\in\mathbb Z$ байна.

a = 1

b = 2

cd = 98

e = 1

f = 3

Бодлогын төрөл: Нөхөх

Амжилтын хувь: 20.79%

Заавар: $\cos(2x-\pi)=\cos(\pi-2x)=-\cos2x$ тул $f(x)=\cos4x-\cos2x$ байна.

$y=\cos ax-\cos bx$ функцийн үе нь $c\pi$ байна. Энд $c$ нь $a$ ба $b$ тоонуудын хамгийн бага эерэг давталт байна.
$c=\cos2x$ гэвэл $\cos4x=2\cos^22x-1=2c^2-1$ тул $f(x)=g(c)=2c^2-c-1$, $-1\le c\le 1$ болно. $\max f(x)=\max g(c)$ байх тул $g(c)$ функцийн хамгийн их утгыг ол.
$g(c)$ функцийн хамгийн бага утгыг ол.
$g(c)=0$ тэгшитгэлийг бод. Мөн $$\cos\alpha-\cos\beta=-2\sin\frac{\alpha-\beta}{2}\sin\frac{\alpha+\beta}{2}$$ томьёо ашиглан үржигдэхүүнд задлан бодож болно.

Бодолт:

$\dfrac12$, $1$ тоонуудын хамгийн бага ерөнхий давталт нь $1$ тул үе нь $\pi$ байна.
$g(c)=2c^2-c-1$, $-1\le c\le 1$ нь $c=-1$ цэг дээр хамгийн их утгаа авна.
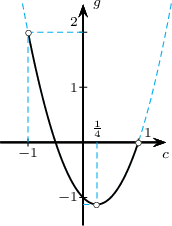
$g(c)=2\Big(c-\dfrac14\Big)^2-\dfrac{9}{8}$ функцийн хамгийн бага утга $c=\dfrac{1}{4}$ үед $-\dfrac98$ байна.
$g(c)=2c^2-c-1=0\Rightarrow c_1=0$, $c_2=-\dfrac12$ байна. Иймд $2x=2\pi k\Rightarrow x=\pi k$ ба $$2x=\pm\arccos(-0.5)+2\pi k=\pm\dfrac{2\pi}{3}+2\pi k\Rightarrow x=\pm\dfrac{\pi}{3}+\pi k$$ байна.