Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Гурвалжны талбай
$A(4,3)$, $B(-3,5)$, $C(0,-3)$ бол $\triangle ABC$-ийн талбайг ол.
A. 25
B. 26
C. 28
D. 30
E. 31
Бодлогын төрөл: Сонгох
Амжилтын хувь: 66.33%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Координатын хавтгай дээр зурж үзээд багтаасан тэгш өнцөгтийн талбайгаас гурвалжны гадна талд орших тэгш өнцөгт гурвалжнуудын талбайг хасаад ол.
Шууд $A(x_1,y_1)$, $B(x_2,y_2)$, $C(x_3,y_3)$ бол $$S_{\triangle ABC}=\dfrac12|x_1y_2+x_2y_3+x_3y_1-x_1y_3-x_2y_1-x_3y_2|$$ томьёог ашиглаад бодсон ч болно.
Шууд $A(x_1,y_1)$, $B(x_2,y_2)$, $C(x_3,y_3)$ бол $$S_{\triangle ABC}=\dfrac12|x_1y_2+x_2y_3+x_3y_1-x_1y_3-x_2y_1-x_3y_2|$$ томьёог ашиглаад бодсон ч болно.
Бодолт: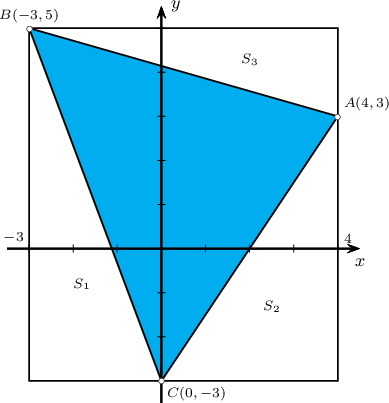 
Том тэгш өнцөгтийн талбай $S=7\cdot 8=56$, $S_1=\dfrac{3\cdot 8}{2}=12$, $S_2=\dfrac{4\cdot6}{2}=12$, $S_3=\dfrac{7\cdot 2}{2}=7$ тул бидний олох талбай
$$S-S_1-S_2-S_3=56-12-12-7=25$$
байна.
Сорилго
2017-09-18
11-12 анги математик
4.29
Координатын арга.
Хавтгайн координатын арга.
КООРДИНАТЫН АРГА
координатын геометр
2 цэгийн хоорондох зай
Хувиргалт