Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
ЭЕШ 2013 A №21
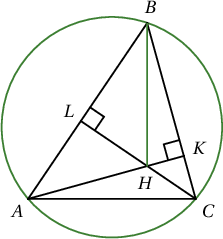
$ABC$ гурвалжны $A$ ба $C$ оройн өндрүүд $H$ цэгт огтлолцоно. Хэрэв $ABC$ гурвалжныг багтаасан тойргийн радиус $4$ нэгж ба $\sin\angle BAH=\dfrac25$ бол $|BH|=?$
A.$3\dfrac56$ B.$3\dfrac15$ C.$3\dfrac78$ D.$3$ E.$3\dfrac13$
Бодлогын төрөл:Сонгох
Амжилтын хувь:33.08%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:$BH=2R\cos\beta$ болохыг харуул.
Бодолт:$AH$ ба $BC$ огтлолыг $K$, $\angle BAH=\beta, \angle BCA=\gamma$ гэе.
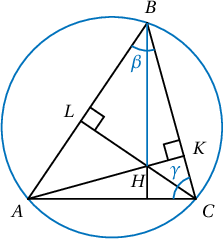$\triangle AKB$ тэгш өнцөгт гурвалжнаас $BK=AB\cos\beta$, $\angle HBK=90^\circ-\gamma$ ба $\triangle BKH$ тэгш өнцөгт гурвалжин тул
$$BH=\dfrac{BK}{\cos(90^\circ-\gamma)}=\dfrac{AB\cos\beta}{\sin\gamma}=2R\cos\beta$$
болно. $\beta=90^\circ-\angle BAH$ тул $\cos\beta=\sin\angle BAH=\dfrac{2}{5}$. Иймд
$$BH=2R\cos\beta=2\cdot4\cdot\dfrac{2}{5}=3\dfrac{1}{5}$$
Сорилго
ЭЕШ 2013 A hw-56-2016-06-15 Синусын теорем ЭЕШ гурвалжин ЭЕШ-2013 A alias geometr Хавтгайн геометр 1 Дунд сургуулийн геометр Дунд сургуулийн геометр Синусын теорем Гурвалжны өндөр Гурвалжны өндөр ЭЕШ 2013 A тестийн хуулбар ЭЕШ 2013 A тестийн хуулбар Хавтгайн геометр 1 тестийн хуулбар ЭЕШ 2013 A Геометр тойм